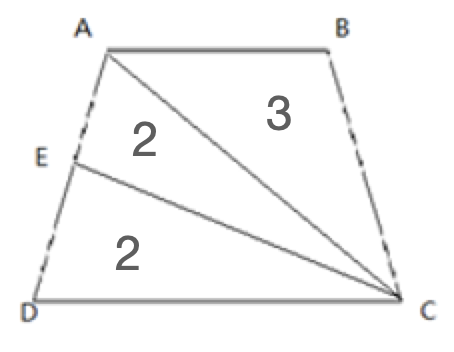
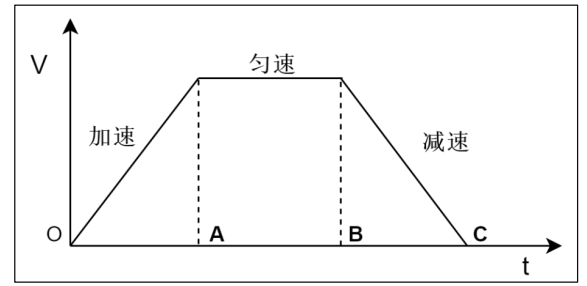
本文主要是介绍Trapezoidal numerical integration(梯形数值积分),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
**1. Trapezoidal numerical integration(梯形数值积分)
1. Principle*
【trapz】performs numerical integration via the trapezoidal method. This method approximates the integration over an interval by breaking the area down into trapezoids with more easily computable areas. For example, here is a trapezoidal integration of the sine function using eight evenly-spaced trapezoids:

2. Formula
a) the constant spacing model

b) General model
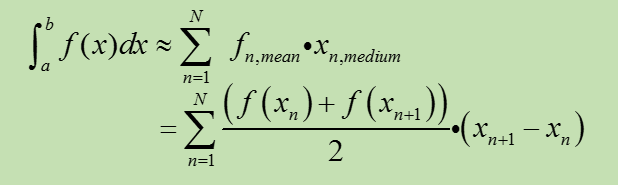
Q = trapz(Y) computes the approximate integral of Y via the trapezoidal method with unit spacing. The size of Y determines the dimension to integrate along:
- If Y is a vector, then trapz(Y) is the approximate integral of Y.
- If Y is a matrix, then trapz(Y) integrates over each column and
returns a row vector of integration values. - If Y is a multidimensional array, then trapz(Y) integrates over the
first dimension whose size does not equal 1. The size of this
dimension becomes 1, and the sizes of other dimensions remain
unchanged.
Q = trapz(X,Y) integrates Y with respect to the coordinates or scalar spacing specified by X.
- If X is a vector of coordinates, then length(X) must be equal to the
size of the first dimension of Y whose size does not equal 1. - If X is a scalar spacing, then trapz(X,Y) is equivalent to
X*trapz(Y).
典例
Integrate Vector of Data with Unit Spacing
Calculate the integral of a vector where the spacing between data points is 1.
Create a numeric vector of data.
Y = [1 4 9 16 25];
Y contains function values for in the domain [1, 5].
Use trapz to integrate the data with unit spacing.
Q = trapz(Y)
This approximate integration yields a value of 42. In this case, the exact answer is a little less, . The trapz function overestimates the value of the integral because f(x) is concave up.
Copyright 2012 The MathWorks, Inc.
这篇关于Trapezoidal numerical integration(梯形数值积分)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!