字典树和基数树

一、字典树

    1、概述

字典树是一种前缀查找树，在前缀匹配查找中应用比较多，查找树的层级取决于字符串长度，时间复杂度O(1)，但是他要求每个节点要有26各分支，所以空间开销比较高，是一种典型的以空间换时间的数据结构。

   2、实现原理

1)、字典树快速查找是依赖于将一个字符串分解成单个字符，然后每个字符单独作为一个节点，按字符串顺序链接，到达单词结尾时做一个结束标记。一个单词构成一个链表，多个单词时相同位置层级的节点可以合并，就能形成一个树，这个树就是字典树。

如上图，字典树要求所有字符串共用一个根起始点，起始点为空不存数据。到达单词结尾点用红色标记。

2)、结构定义

typedef struct Trie
{int count;  /*用于计数当前节点作为末尾的单词数量,同时作为查找时判断单词到达末尾的标记*/Trie *node[26]; /*节点的26个分支*/
}Trie;

3)、实现

 1、初始化

   一棵空Trie仅包含一个根节点，该点的字符指针均指向空

Trie* TrieNodeInit()
{Trie* head = (Trie*)calloc(1, sizeof(Trie));head->count = 0;return head;
}

2、插入

当需要插入一个字符串S时，我们令一个指针P起初指向根节点。然后，一次扫描S中的每个字符c：
    1.当P的c字符指针指向一个已存在的节点Q,则令P=Q。
    2.当P的c字符指针指向空，则新建一个节点Q,令P的c字符指针指向Q,然后令P=Q。
    当S中的字符扫描完毕时，在当前节点P上标记它是一个字符串的末尾。

/*输入的统一是小写26个字母组成的字符串，这里就不做判断了*/
int TrieInsert(char* str, Trie* head)
{char* p = str;Trie* node = head;int idx = 0;/*循环遍历字符串，将每个字符加入到指定节点*/while(*p != '\0'){/*取当前字符相对'a'字符的偏移*/idx = *p - 'a';/*node指向下一层树节点*/node = node[idx];/*如果下一层树为空，则初始化该节点*/if(!node){node = TrieNodeInit(); }p++;}/*此时node处就是该字符串的结尾，结尾标记自增*/node->count++;return 0;
}

3、查找

当需要检索一个字符串S在Trie中是否存在时，我们令一个指针P起初指向根节点，然后一次扫描s中的每个字符c:
    1.若P的c字符指针指向空，则说明S没有被插入过Trie，结束检索。
    2.若P的c字符指针指向一个已经存在的节点Q,则令P=Q。
    当S中的字符扫描完毕时，若当前节点P被标记为一个字符串的末尾，则说明S在Trie中存在，否则说明S没有被插入过Trie.
    可以看出在Trie中，字符数据都体现在树的边（指针）上，树的节点仅保存一些额外信息。例如单词结尾标记等。

int TrieSearch(Trie* head, const char* str)
{char* p = str;Trie* node = head;int idx = 0;while(*p != '\0'){idx = *p - 'a';node = node[idx];/*当前字符串不在树内，直接返回0*/if(!node)return 0;p++;}/*返回当前字符串计数个数*/return node->count;
}

3、字典树的应用

（1） 字符串检索
事先将已知的一些字符串（字典）的有关信息保存到trie树里，查找另外一些未知字符串是否出现过或者出现频率。

（2）文本预测

trie树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

（3）词频统计

统计加入字典树内的每个单词的计数

（4）排序

Trie树是一棵多叉树，只要先序遍历整棵树，输出相应的字符串便是按字典序排序的结果。
比如给你N 个互不相同的仅由一个单词构成的英文名，让你将它们按字典序从小到大排序输出。

（5）字符串最长公共前缀
Trie树利用多个字符串的公共前缀来节省存储空间，当我们把大量字符串存储到一棵trie树上时，我们可以快速得到某些字符串的公共前缀。

二、基数树

1、概述

radix Tree(基数树) 其实就差不多是传统的二叉树，只是在寻找方式上，利用比如一个unsigned int的类型的每一个比特位作为树节点的判断。 可以这样说，比如一个数1000101010101010010101010010101010，那么按照Radix 树的插入就是在根节点，如果遇到0，就指向左节点，如果遇到1就指向右节点，在插入过程中构造树节点，在删除过程中删除树节点
（使用一个比特位判断，会使树的高度过高，非叶节点过多。故在实际应用中，我们一般是使用多个比特位作为树节点的判断，但多比特位会使节点的子节点槽变多，增大节点的体积，一般选用2个或4个比特位作为树节点即可） 

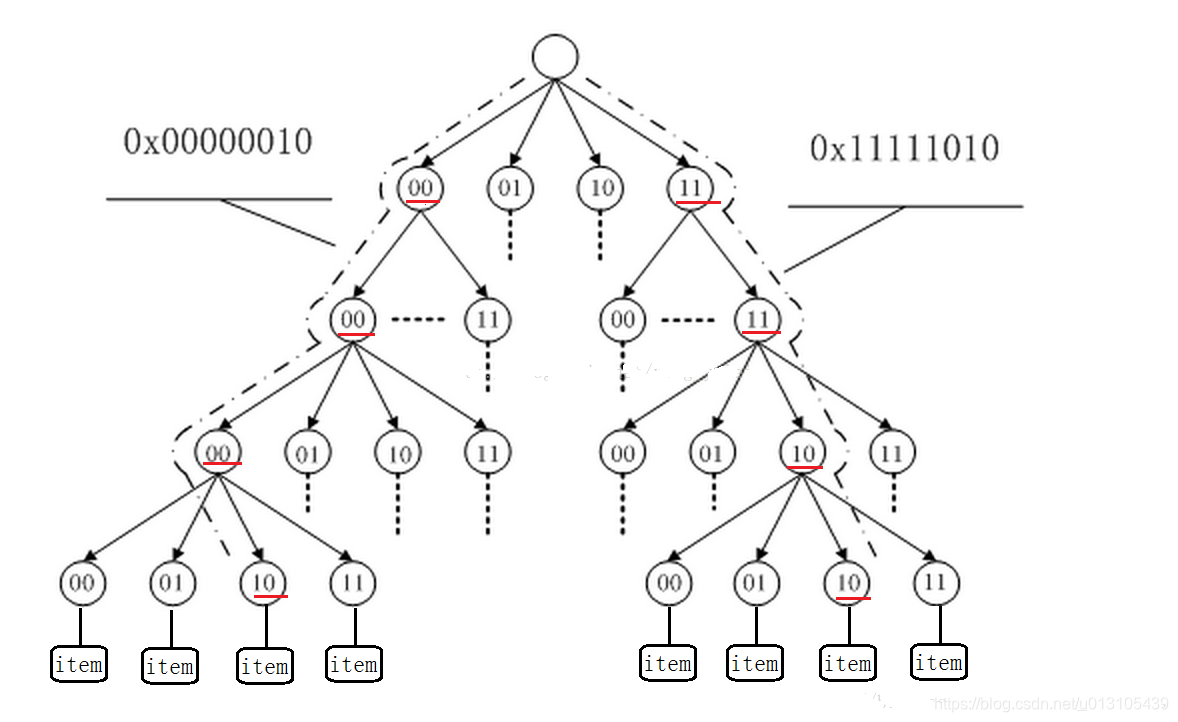
2、作用

基数树（radix tree）是将long整数与指针键值相关联的机制，它存储有效率，并且可快速查询，用于整数值与指针的映射，对于长整型数据的映射，如何解决Hash冲突和Hash表大小的设计是一个很头疼的问题，利用radix树可以根据一个长整型（比如一个长ID）快速查找到其对应的对象指针。这比用hash映射来的简单，也更节省空间，使用hash映射hash函数难以设计，不恰当的hash函数可能增大冲突，或浪费空间。

基数树和字典树的实现机制很像，都是将key拆分成一部分映射到树形结构中，基数树是将key按指针地址bit位拆分，而字典树是将key的字符串值按字符拆分。但是基数树的层高是相对固定的(因为指针地址的bit位是固定的)，而字典树的高度与字符串的长度相关，而树的高度决定了树的空间占用情况，所以基数树明显更节约空间。