本文主要是介绍自然激励技术 (NExT) 与特征系统实现算法 (ERA)(Matlab代码实现),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🌈3 Matlab代码实现
🎉4 参考文献
💥1 概述
本文使用时域NExT和频域NExT的特征系统实现算法(ERA)的自然激励技术(NExT)。
用于识别受高斯白噪声激励影响的2DOF系统,并增加激励和响应的不确定性(也是高斯白噪声)。
[Result] = NExTTERA(data,refch,maxlags,fs,ncols,nrows,cut,shift,EMAC_option)
输入 :data:
包含响应数据的数组,其维度为 (nch,Ndata),其中 nch 是通道数。Ndata 是数据
引用的总长度: 参考通道的 vecor .its 维度 (numref,1) 其中 numref 是参考通道
的数量 maxlags: 互相关函数
fs 中的滞后数: 采样频率
ncols: 汉克尔矩阵中的列数(超过 2/3*numref*(maxlags+1) )nrows: 汉克尔矩阵中的行数(超过 20 * 模式数)
剪切: 截止值=2*模式
数 移位:最后一行和列块中的移位值(增加 EMAC 灵敏度)通常 =10
EMAC_option:如果此值等于 1,则 EMAC 将与列数无关(仅根据可观测性矩阵计算,而不是根据可控性计算)输出:
结果:结构由以下组件
组成 参数: NaFreq : 固有频率矢量 阻尼比: 阻尼比矢量
模态形状: 振型矩阵 指标: MAmC : 模态振幅相干
EMAC: 扩展模态振幅相干
MPC: 模态相位共线性
CMI: 一致模式指示器
部分: 参与因子
矩阵 A、B、C: 离散 A、B 和 C 矩阵
[结果] = NExTFERA(data,refch,window,N,p,fs,ncols,nrows,cut,shift,EMAC_option)
输入:
data:包含响应数据的数组,其维度为 (nch,Ndata),其中 nch 是通道数。Ndata 是数据
的总长度 refch: 参考通道的 vecor .its 尺寸 (numref,1) 其中 numref 是参考通道
的数量 窗口:窗口大小以获得光谱密度
N:窗口数 p:窗口
之间的重叠比率。从 0 到 1
fs: 采样频率
ncols: 汉克尔矩阵中的列数(大于 2/3*数字参考*(ceil(窗口/2+1)-1) )nrows: 汉克尔矩阵中的行数(超过 20 * 模式数)cut: 截止值=2*模式
数 移位:最后一行和列块中的移位值(增加 EMAC 灵敏度)
通常 =10
EMAC_option:如果此值等于 1,则 EMAC 将与列数无关(仅根据可观测性矩阵计算,而不是根据可控性计算)输出:
结果:结构由以下组件
组成 参数: NaFreq : 固有频率矢量 阻尼比: 阻尼比矢量
模态形状: 振型矩阵 指标: MAmC : 模态振幅相干
EMAC: 扩展模态振幅相干
MPC: 模态相位共线性
CMI: 一致模式指示器
部分: 参与因子
矩阵 A、B、C: 离散 A、B 和 C 矩阵
📚2 运行结果


🌈3 Matlab代码实现
部分代码:
%Apply modal superposition to get response
%--------------------------------------------------------------------------
n=size(f,1);
dt=1/fs; %sampling rate
[Vectors, Values]=eig(K,M);
Freq=sqrt(diag(Values))/(2*pi); % undamped natural frequency
steps=size(f,2);
Mn=diag(Vectors'*M*Vectors); % uncoupled mass
Cn=diag(Vectors'*C*Vectors); % uncoupled damping
Kn=diag(Vectors'*K*Vectors); % uncoupled stifness
wn=sqrt(diag(Values));
zeta=Cn./(sqrt(2.*Mn.*Kn)); % damping ratio
wd=wn.*sqrt(1-zeta.^2);
fn=Vectors'*f; % generalized input force matrix
t=[0:dt:dt*steps-dt];
for i=1:1:n
h(i,:)=(1/(Mn(i)*wd(i))).*exp(-zeta(i)*wn(i)*t).*sin(wd(i)*t); %transfer function of displacement
hd(i,:)=(1/(Mn(i)*wd(i))).*(-zeta(i).*wn(i).*exp(-zeta(i)*wn(i)*t).*sin(wd(i)*t)+wd(i).*exp(-zeta(i)*wn(i)*t).*cos(wd(i)*t)); %transfer function of velocity
hdd(i,:)=(1/(Mn(i)*wd(i))).*((zeta(i).*wn(i))^2.*exp(-zeta(i)*wn(i)*t).*sin(wd(i)*t)-zeta(i).*wn(i).*wd(i).*exp(-zeta(i)*wn(i)*t).*cos(wd(i)*t)-wd(i).*((zeta(i).*wn(i)).*exp(-zeta(i)*wn(i)*t).*cos(wd(i)*t))-wd(i)^2.*exp(-zeta(i)*wn(i)*t).*sin(wd(i)*t)); %transfer function of acceleration
qq=conv(fn(i,:),h(i,:))*dt;
qqd=conv(fn(i,:),hd(i,:))*dt;
qqdd=conv(fn(i,:),hdd(i,:))*dt;
q(i,:)=qq(1:steps); % modal displacement
qd(i,:)=qqd(1:steps); % modal velocity
qdd(i,:)=qqdd(1:steps); % modal acceleration
end
x=Vectors*q; %displacement
v=Vectors*qd; %vecloity
a=Vectors*qdd; %vecloity
%Add noise to excitation and response
%--------------------------------------------------------------------------
f2=f+0.1*randn(2,10000);
a2=a+0.1*randn(2,10000);
v2=v+0.1*randn(2,10000);
x2=x+0.1*randn(2,10000);
%Plot displacement of first floor without and with noise
%--------------------------------------------------------------------------
figure;
subplot(3,2,1)
plot(t,f(1,:)); xlabel('Time (sec)'); ylabel('Force1'); title('First Floor');
subplot(3,2,2)
plot(t,f(2,:)); xlabel('Time (sec)'); ylabel('Force2'); title('Second Floor');
subplot(3,2,3)
plot(t,x(1,:)); xlabel('Time (sec)'); ylabel('DSP1');
subplot(3,2,4)
plot(t,x(2,:)); xlabel('Time (sec)'); ylabel('DSP2');
subplot(3,2,5)
plot(t,x2(1,:)); xlabel('Time (sec)'); ylabel('DSP1+Noise');
subplot(3,2,6)
plot(t,x2(2,:)); xlabel('Time (sec)'); ylabel('DSP2+Noise');
%Identify modal parameters using displacement with added uncertainty
%--------------------------------------------------------------------------
data=x2;
refch=2;
maxlags=999;
window=2000;
N=5;
p=0;
ncols=800;
nrows=200;
cut=4;
shift=10;
EMAC_option=1;
[Result1] = NExTFERA(data,refch,window,N,p,fs,ncols,nrows,cut,shift,EMAC_option);
[Result2] = NExTTERA(data,refch,maxlags,fs,ncols,nrows,cut,shift,EMAC_option);
%Plot Impulse Response Functions
%--------------------------------------------------------------------------
IRFT= NExTT(data,refch,maxlags);
IRFF= NExTF(data,refch,window,N,p);
t2=[0:dt:999*dt];
figure;
subplot(2,2,1)
plot(t2,IRFT(1,:)); xlabel('Time (sec)'); ylabel('IRF1'); title('NExTT');
subplot(2,2,2)
plot(t2,IRFF(1,:)); xlabel('Time (sec)'); ylabel('IRF1'); title('NExTF');
subplot(2,2,3)
plot(t2,IRFT(2,:)); xlabel('Time (sec)'); ylabel('IRF2');
subplot(2,2,4)
plot(t2,IRFF(2,:)); xlabel('Time (sec)'); ylabel('IRF2');
%Plot real and identified first modes to compare between them
%--------------------------------------------------------------------------
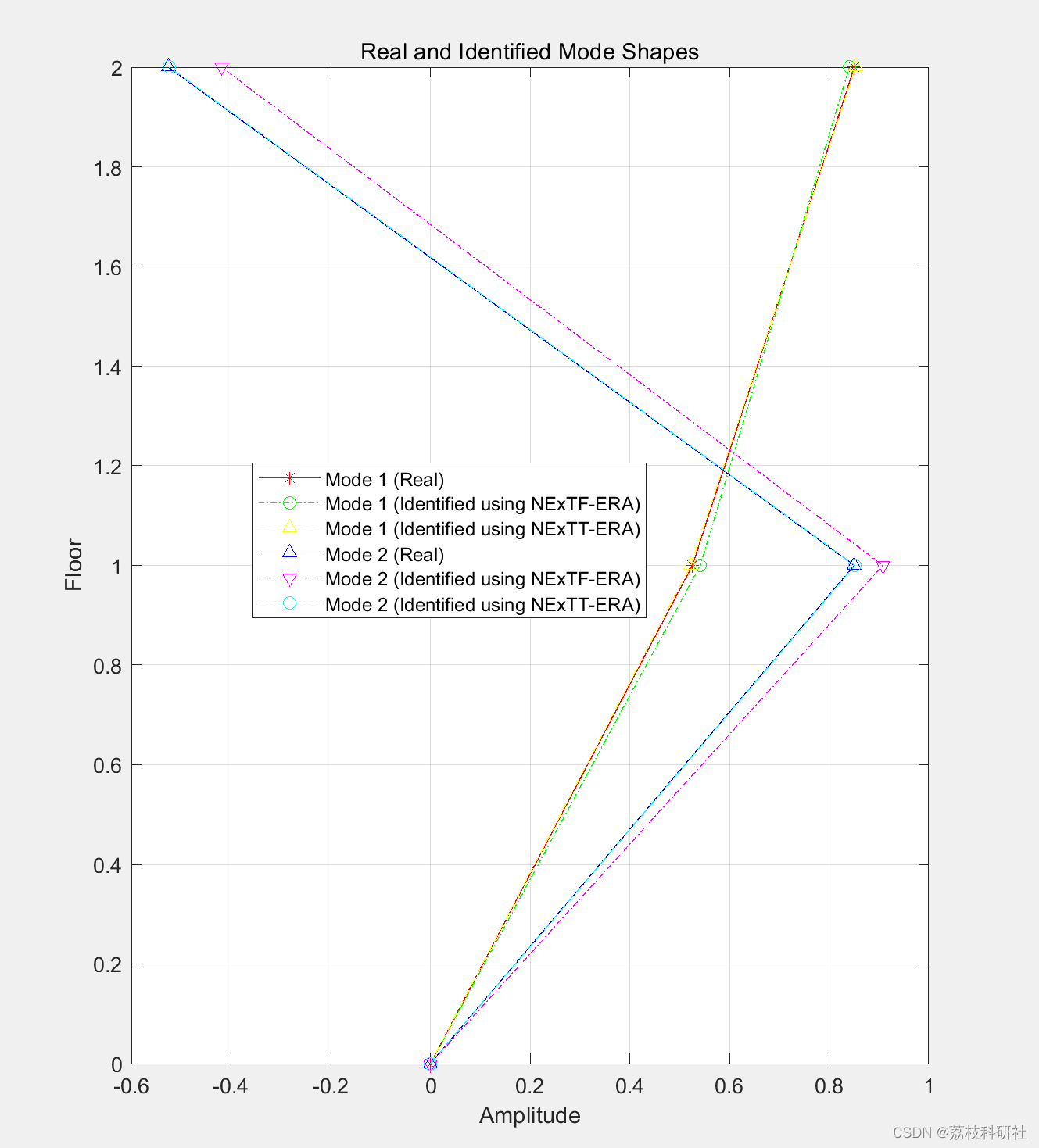
figure;
plot([0 ; -Vectors(:,1)],[0 1 2],'r*-');
hold on
plot([0 ;Result1.Parameters.ModeShape(:,1)],[0 1 2],'go-.');
hold on
plot([0 ;Result2.Parameters.ModeShape(:,1)],[0 1 2],'y^--');
hold on
plot([0 ; -Vectors(:,2)],[0 1 2],'b^-');
hold on
plot([0 ;Result1.Parameters.ModeShape(:,2)],[0 1 2],'mv-.');
hold on
plot([0 ;Result2.Parameters.ModeShape(:,2)],[0 1 2],'co--');
hold off
title('Real and Identified Mode Shapes');
legend('Mode 1 (Real)','Mode 1 (Identified using NExTF-ERA)','Mode 1 (Identified using NExTT-ERA)'...
,'Mode 2 (Real)','Mode 2 (Identified using NExTF-ERA)','Mode 2 (Identified using NExTT-ERA)');
xlabel('Amplitude');
ylabel('Floor');
grid on;
daspect([1 1 1]);
%Display real and Identified natural frequencies and damping ratios
%--------------------------------------------------------------------------
disp('Real and Identified Natural Drequencies and Damping Ratios of the First Mode');
disp(strcat('Real: Frequency=',num2str(Freq(1)),'Hz',' Damping Ratio=',num2str(zeta(1)*100),'%'));
disp(strcat('NExTF-ERA: Frequency=',num2str(Result1.Parameters.NaFreq(1)),'Hz',' Damping Ratio=',num2str(Result1.Parameters.DampRatio(1)),'%'));
disp(strcat('CMI of The Identified Mode=',num2str(Result1.Indicators.CMI(1)),'%'));
disp(strcat('NExTT-ERA: Frequency=',num2str(Result2.Parameters.NaFreq(1)),'Hz',' Damping Ratio=',num2str(Result2.Parameters.DampRatio(1)),'%'));
disp(strcat('CMI of The Identified Mode=',num2str(Result2.Indicators.CMI(1)),'%'));
disp('-----------')
🎉4 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] R. Pappa, K. Elliott, and A. Schenk, “A consistent-mode indicator for the eigensystem realization algorithm,” Journal of Guidance Control and Dynamics (1993), 1993.
[2] R. S. Pappa, G. H. James, and D. C. Zimmerman, “Autonomous modal identification of the space shuttle tail rudder,” Journal of Spacecraft and Rockets, vol. 35, no. 2, pp. 163–169, 1998.
[3] James, G. H., Thomas G. Carne, and James P. Lauffer. "The natural excitation technique (NExT) for modal parameter extraction from operating structures." Modal Analysis-the International Journal of Analytical and Experimental Modal Analysis 10.4 (1995): 260.
[4] Al Rumaithi, Ayad, "Characterization of Dynamic Structures Using Parametric and Non-parametric System Identification Methods" (2014). Electronic Theses and Dissertations. 1325.
[5] Al-Rumaithi, Ayad, Hae-Bum Yun, and Sami F. Masri. "A Comparative Study of Mode Decomposition to Relate Next-ERA, PCA, and ICA Modes." Model Validation and Uncertainty Quantification, Volume 3. Springer, Cham, 2015. 113-133.
这篇关于自然激励技术 (NExT) 与特征系统实现算法 (ERA)(Matlab代码实现)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



