hdu 2211:杀人游戏（递归）

本文主要是介绍hdu 2211:杀人游戏（递归），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

hdu 2211:杀人游戏（递归）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2211

Problem Description

不知道你是否玩过杀人游戏，这里的杀人游戏可没有法官，警察之类的人，只有土匪，现在已知有N个土匪站在一排，每个土匪都有一个编号，从1到N，每次杀人时给定一个K值，从还活着的土匪中，编号从小到大的找到K个人，然后杀掉，继续往下，直到找遍，然后继续从剩下的土匪中，编号从小到大找到第K个活着的土匪，然后杀掉。比如，现在有10个土匪，K为3，第一次杀掉3，6，9号的土匪，第二次杀掉4，8号土匪，第三次杀掉5号土匪，第四次杀掉7号土匪，第五次杀掉10号土匪，我们看到10号土匪是最后一个被杀掉的（从1到K-1的土匪运气好，不会被杀！）。现在给定你一个N和一个K，问你最后一个被杀掉的土匪的编号是多少。

Input

第一行有一个T（T<=10000），接下来有T组数据，每组中包含一个N（N<2^31）和一个K（3<=K<=100&&K<N）。

Output

对于每组数据，输出最后被杀的土匪的编号。

Sample Input

1
10 3

Sample Output

又是一道烧脑题，这种题谁受得了啊，找不到突破口寸步难行，找到了水的要死。。。。

以下题解参考这位博主的博客：传送门

★先说递归思想：递推关系+边界条件，二者缺一不可。这道题的递推关系是根据前一轮胜利者的编号确定当前轮胜利者的编号，一直递推下去到最后一轮（也就是边界条件），胜利者在1,2,3，……，k-1,k的第k个位置上。即n==k时，返回k.

★再说整除方程（返回值的确定）。

如果你查阅相关结题报告，凡是递归解决的无外乎这样一段话：
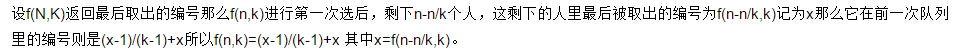
在这里插入图片描述

这句话只是结论呦，推导看我的吧~

设上一轮胜利者的编号为x,当前轮胜利者的编号为y,容易推到得到这样的一个方程：y=y/k+x
式子意义是当前编号=这一轮在y之前被杀死的数量+上一轮在y之前剩下的数量x
注意，这可不是一般的方程哦，/表示的是整除，不要左右同×k，结果不等价的。
这样的方程笔者姑且叫她整除方程吧，利用不等式求解。求解思路如下：
●Step1 首先观察到y无法直接求解，不妨先求y/k，设m=y/k,则y=m+x(x已知)，问题转化为求整除结果m.
●Step2 由y/k=m有，m·k+1<=y<=m·k+(k-1).为什么是m·k+1<=y而不是m·k<=y,因为y表示的是当前这轮胜利者的编号，不到最后一轮不会出现y%k==0的情况（最后一轮已经被返回了）。令y=m+x,代入得到
m·k+1<=m+x<=m·k+(k-1)，原不等式组等价于

m·（k-1）<=x-1<=m·（k-1）+(k-2）.

看出来没有？？！！！把她反一下就可以表示为m=(x-1)/(k-1),两者表示的含义是不是等价的？？？？！！！！Yes!!
那么m就求出来啦.则y=y/k+x=m+x=(x-1)/(k-1)+x 了，参考递归代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
/**递归函数*/
int fx(int n,int k)
{if(n==k)       //递归条件return k;int x=fx(n-n/k,k);     //胜利者在下一个子序列的编号记为：xreturn (x-1)/(k-1)+x;        //那么这一轮编号为y=y/k+x;
}
int main()
{int t;int n,k;      //即：题目所说的土匪总数，以及每次所杀的区间scanf("%d",&t);while(t--){scanf("%d%d",&n,&k);int num;/**调用函数*/num=fx(n,k);printf("%d\n",num);}return 0;
}