本文主要是介绍信息学奥赛一本通:1196:踩方格,为什么n=3时17种,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【题目描述】
有一个方格矩阵,矩阵边界在无穷远处。我们做如下假设:
a、每走一步时,只能从当前方格移动一格,走到某个相邻的方格上;
b、走过的格子立即塌陷无法再走第二次;
c、只能向北、东、西三个方向走;
请问:如果允许在方格矩阵上走n步,共有多少种不同的方案。2种走法只要有一步不一样,即被认为是不同的方案。
【输入】
允许在方格上行走的步数n(n≤20)。
【输出】
计算出的方案数量。
【输入样例】
2
【输出样例】
7
【题目分析】


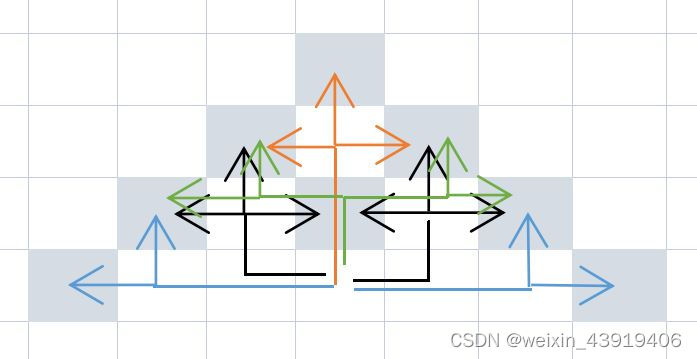
【方法1】递推:
如果走一步,有3种;如果走2步,有7种走法;如果走三步有17种。如果上一步是向上的,可以左右上;上一步是向左的,只能上左;上一步是向右的,只能上右。设up[i]表示向上,left[i]表示向左,right[i]表示向右,则up[i]=up[i-1]+left[i-1]+right[i-1],left[i]=left[i-1]+up[i-1],right[i]=right[i-1]+up[i-1]。
#include <bits/stdc++.h>
using namespace std;
int l[21],r[21],u[21];
int main()
{int n;cin>>n;l[1]=1,r[1]=1,u[1]=1;for(int i=2;i<=n;i++){l[i]=l[i-1]+u[i-1];r[i]=r[i-1]+u[i-1];u[i]=u[i-1]+r[i-1]+l[i-1];}cout<<l[n]+r[n]+u[n];return 0;
}
方法2:递推
设a[i]为第走i步有几种走法,a[i]=left[i]+right[i]+up[i]=left[i-1]+up[i-1]+right[i-1]+up[i-1]+left[i-1]+up[i-1]+right[i-1]=2*(left[i-1]+up[i-1]+right[i-1)+up[i-1]=2*a[i-1]+up[i-1]=2*a[i-1]+(left[i-2]+right[i-2]+up[i-2])=2*a[i-1]+a[i-2]
#include <bits/stdc++.h>
using namespace std;
int a[21];
int main()
{int n;cin>>n;a[1]=3;a[2]=7;for(int i=3;i<=n;i++){a[i]=2*a[i-1]+a[i-2];}cout<<a[n];return 0;
}方法3:递归
#include <bits/stdc++.h>
using namespace std;
int f(int n){if (n==1) return 3;if (n==2) return 7;return 2*f(n-1)+f(n-2);
}
int main()
{int n;cin>>n;cout<<f(n)<<endl;return 0;
}
这篇关于信息学奥赛一本通:1196:踩方格,为什么n=3时17种的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!