poj3281-二分图-最大流

题意就是给N头牛，F个食物，D个饮料，每头牛喜欢的食物和饮料各不相同。一头牛需要吃到饭和饮料才能满足，问你最多满足多少头牛。

其实二分图难的并不是算法，而是其构图过程。
如果是简单的分配食物直接用二分图匹配就行，但现在要同时给一头牛分配饮料和食物，我们可以通过题目中给的信息，先画出来牛与食物和饮料的关系图。如图：

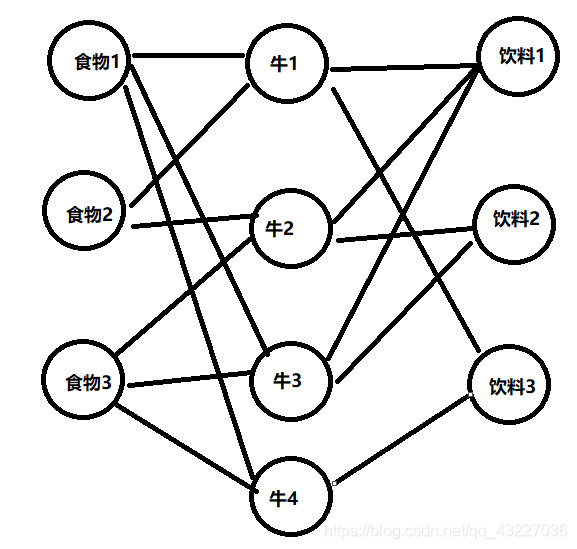
看到这个图大家可能有一点感觉了，这在加一个s, t不就是一个求权值为1的最大流问题嘛。
如图：

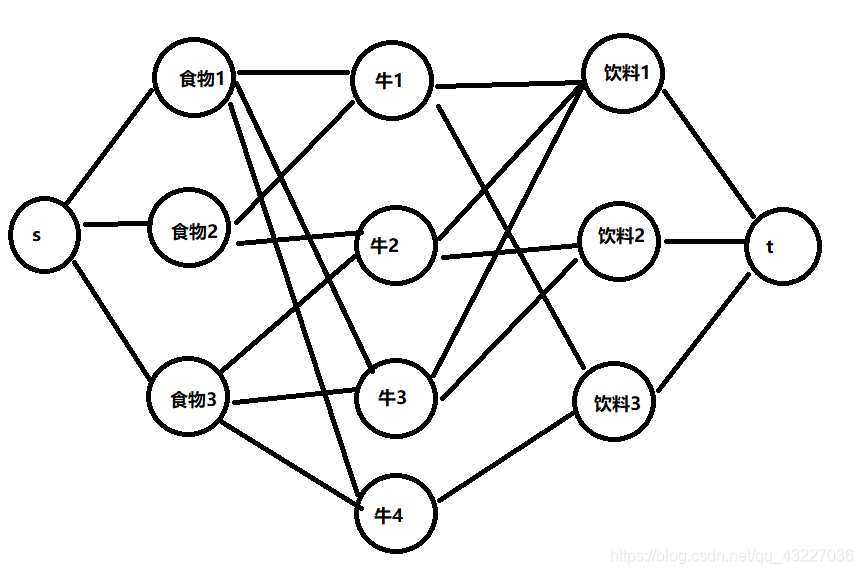
可能许多人觉得这样就结束了，那我建议你去打一下代码，提交一下看看能不能过。
我就是以为这样就可以了，但是提交后就wa了，我仔细想了想知道了为什么，因为就拿牛1来说，只需要给他一份食物后，就要继续去找饮料了，它只需要一份食物。上面图得缺点就在于当到达牛这个节点去dfs得时候，本应该只找饮料，但还是会往回找食物。所以就应该像下面这么建图：
达到源点->食物->牛->牛->饮料->汇点

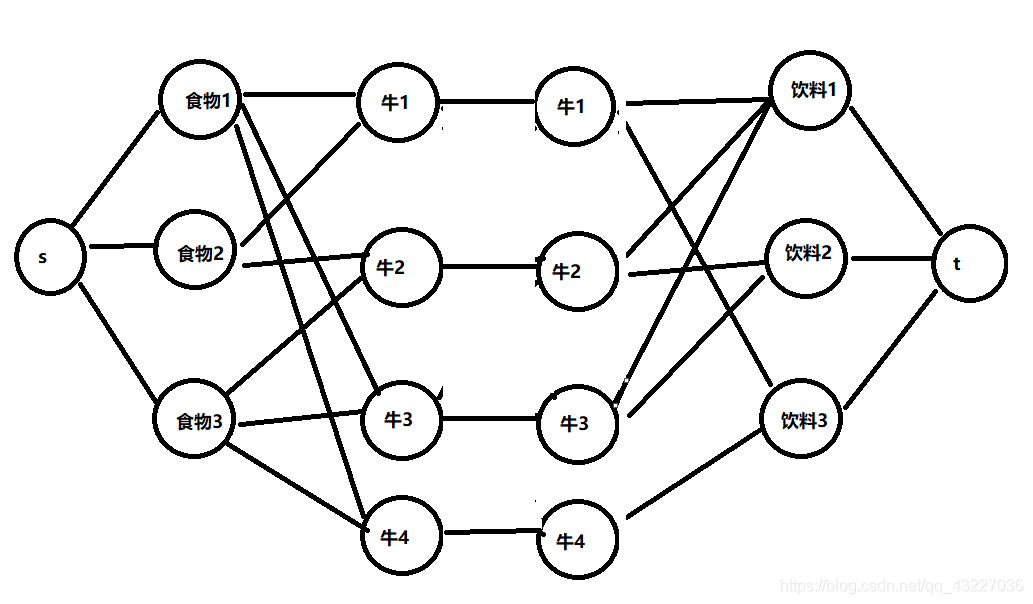
一定要注意，构图非常重要，下面代码用ff，嫌慢得小伙伴可自行更改为dicnic
AC代码：

#include <iostream>
#include <vector>
#include <cstring> using namespace std;
const int MAX_N = 500001;
const int INF = 0x3f3f3f3f;struct edge
{int to, cap, rev;
};bool used[MAX_N];
vector <edge>G[MAX_N]; //用邻接表来存储图
int N, F, D;void add_edge(int from, int to, int cost)
{struct edge e = {to, cost, G[to].size()};G[from].push_back(e);struct edge v = {from, 0, G[from].size()-1};G[to].push_back(v);
}//深搜查找增广路
int dfs(int v, int t, int f)
{if (v == t){return f;}used[v] = true;for (int i=0; i<G[v].size(); i++){edge &e = G[v][i];if (!used[e.to] && e.cap > 0){int d = dfs(e.to, t, min(e.cap, f));if (d > 0){e.cap -= d;G[e.to][e.rev].cap+=d;return d;}}}return 0;
}//ff最大流算法
int max_flow(int s, int t)
{int flow = 0;for (;;){memset(used, 0, sizeof(used));int d = dfs(s, t, INF);if (d == 0){return flow;}flow += d;}
}void slove()
{//添加的源点和汇点int s = N*2 + F + D, t = s + 1;//0~N-1是左侧牛//N~N*2-1是右侧牛//N*2~N*2+F-1是食物//N*2+F~N*2+F+D-1是饮料//添加源点和食物得边for (int i=0; i<F; i++){add_edge(s, N*2+i, 1);}//添加饮料和汇点得边for (int i=0; i<D; i++){add_edge(N*2 + F + i, t, 1);}//添加牛与牛之间得边for (int i=0; i<N; i++){add_edge(i, N+i, 1);}//添加食物和饮料与牛得边for (int i=0; i<N; i++){int a, b;scanf("%d %d", &a, &b);for (int j=0; j<a; j++){int x;scanf("%d", &x);x--;add_edge(N*2+x, i, 1);}for (int j=0; j<b; j++){int x;scanf("%d", &x);x--;	add_edge(N+i, N*2+F+x, 1);}}printf("%d\n", max_flow(s, t));
}int main()
{scanf("%d %d %d", &N, &F, &D);slove();return 0;
}