本文主要是介绍GraphSage与DGL实现同构图 Link 预测,通俗易懂好文强推,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
GraphSage与DGL实现同构图 Link 预测,通俗易懂好文强推
文章源码下载地址:点我下载http://inf.zhihang.info/resources/pay/7692.html
书接上文,在作者以前的文章 graphSage还是HAN ?吐血力作综述Graph Embeding 经典好文 和 一文揭开图机器学习的面纱,你确定不来看看吗 ,我们已经了解到 图机器学习/深度学习 的基础知识,我们知道了图数据结构是由 节点和边 组成,这是图在 数据结构与数学中 的定义,我们一般把图用来进行 复杂场景中的关系建模 。但是在算法工程师们实际使用图的过程中,图又处于什么角色呢? 让我们在接下来的一段时间一起来深入其中具体揭秘吧~
当我们用 图结构 来对现实中的事物进行关系建模的时候,则 节点 可以是任何同构图或则异构图中占据 关系二元性 一点的item ID( 无论如何复杂的群体关系均可以把拆解成两两之间多种关系的组合 ),这个item可以是 微博社交 场景中的用户,也可以是 京东淘宝电商购买 场景中的商品或买家与卖家。甚至在异常检测的场景中,我们也会把设备id, ip 等属性构建成异构图节点的一种,毕竟在 互联网上聚集在很大概率上就意味着异常 , 而风控中属性的聚集更为常见。如下图所示:
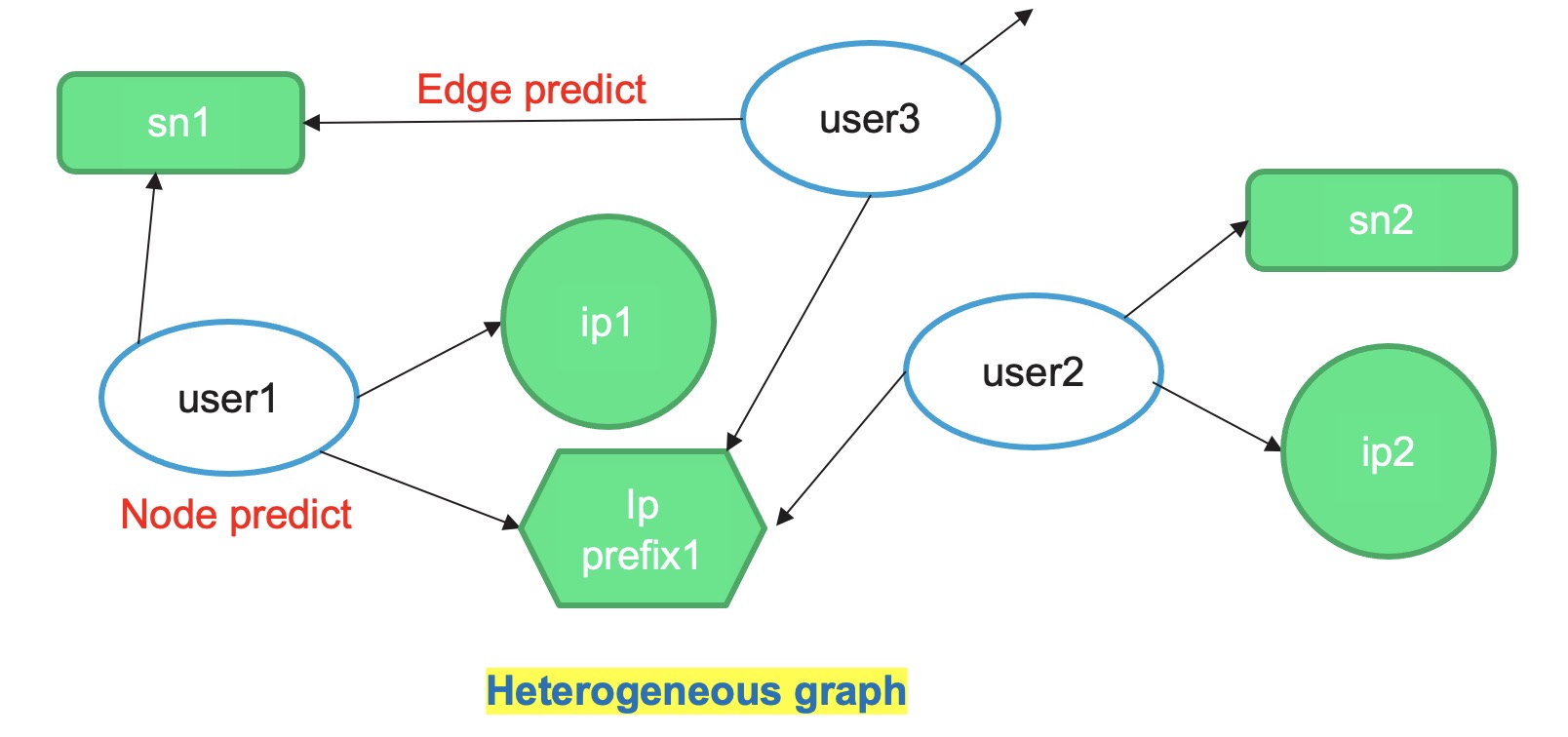
而在 一文揭开图机器学习的面纱,你确定不来看看吗 一文中,我们也介绍了图的多种分类,不熟悉的同学可以先阅读一下上文。
其中有涉及了 同构图和异构图 的概念,文中说:图中节点类型和边类型超过两种的图称为异构图 ,而图中的边在实际建模过程中就用来表示两种item之间的关系。就像上面微博社交同构图中用户的朋友关系,以及京东淘宝京东电商中的买家与商品的购买关系。这里我们要区分一点就是异构多重图中,两类同2个item之间的关系可以有多种,就像你可以购买了商品,同时你也可以搜藏了商品,那你和同一种商品之间是有两条边的。
一般实际使用中,我们直接从 用户行为日志 中提炼出 两者或两类item ID 之间的联系,例如:用户和产生行为的商品。直接用这样的关系用来构建图中的边,而这两者或两类item ID则用来构建成图中的顶点。
我们在这里 再三强调构图,主要是因为我们训练模型大多数时候就是在 学习图中特征的空间结构关系信息,所以我们一定要 精心设计图的节点和边,不然到最后模型效果不好在从头找原因,就比较麻烦了。
而在 graphSage还是HAN ?吐血力作综述Graph Embeding 经典好文 中,我们也大致介绍了现阶段在图上进行的主流机器学习任务,除了整图预测中的 图读出 ( graph readout ,GR, 整图节点输出为一个综合的图表示embeding)外,我们更多的是去进行 同构图或异构图 中 节点和边 的 分类回归 任务以及 链接预测 。下面,就让我从最简单也最常用的同构图上 Link 预测任务开始吧~
注意:我们这里说的链接 Link 预测,也称 关系预测,目的是预测 两节点之间有是否有边存在 。而 边分类与回归,则是去预测边是属于哪种类型的边,以及去预测边上的属性值。例如:图上的边分类与回归预测的可以是购买了衣服还是搜藏的衣服,以及会买几件的这个数值。
(1) 图上有监督与无监督任务的区分
我们知道,通常我们说的 有监督学习 是根据外界对数据特征打的标签来进行学习,是一种给定了答案的学习, 在训练时它的 输入是特征(Feature) 而 输出是标签(Label), 我们期望模型能从特征中学习到 标签约束 下数据模式,让模型知道再次遇到类似的数据应该给它打什么标签。而 无监督学习 ,顾名思义,外界没有对数据特征限定应该学习什么,而是希望模型能在数据集中找出 数据集固有的规律 ,让模型在数据集中进行 自学 ,在训练时它的输出数据一般就是输入数据集自身。而在图上的任务也是如此,如下图所示:
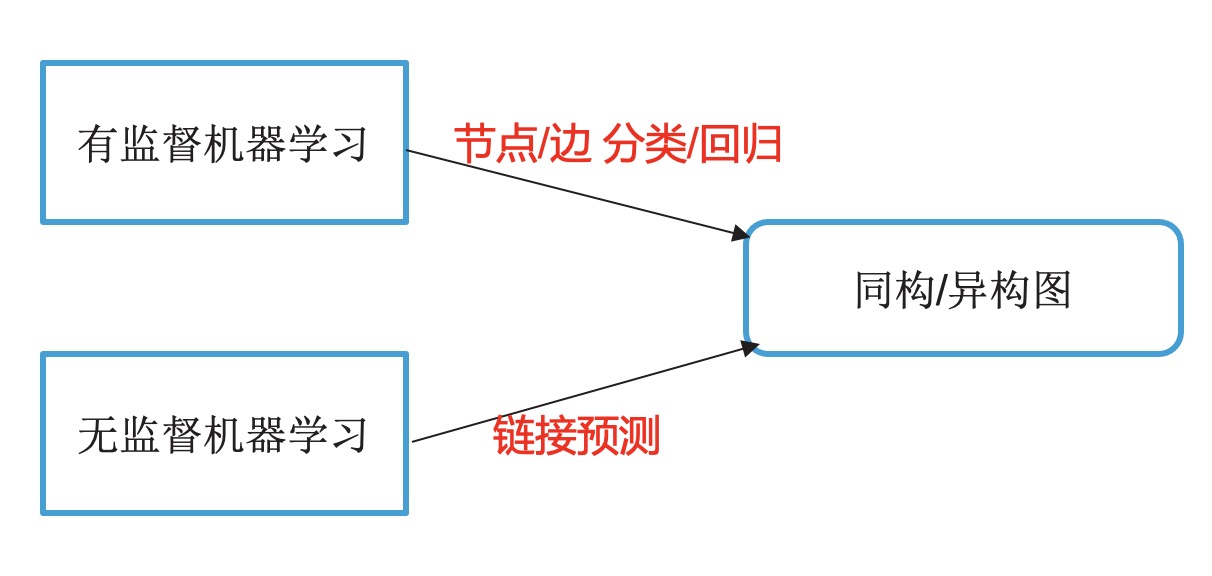
对于 图上的有监督学习 ,就像节点分类任务,我们会给节点一个标签,例如异常检测中,给定一个用户是否异常,然后进行图机器学习/深度学习的训练,让模型根据该训练集中用户的标签学习如何给测试集中没见过的用户打标签,这里的标签是外界输入给定的,模型学习的是标签约束下的数据表达,一般图上的有监督机器学习任务包括:节点分类与回归,边的分类与回归 。而 图上的无监督学习 ,则是不会外界给图上的节点或边标签,而仅仅让模型去学习图结构自身的结构信息,没有外界先验知识的指导,图上的有监督机器学习任务一般包括:链接预测。
熟悉深度学习 模型源码 的同学更是一眼可以看出有监督与无监督模型的差别: 对于有监督学习,通常只需要使用定义好的模型进行前向传播计算,并通过在训练节点上/或边上比较预测和真实标签来计算损失,从而完成 反向传播 。而对于无监督学习,其学习的是数据集本身,迁移到图上也就是图结构自身的信息,通常我们基于假设在图结构中,彼此之间有关系的或则 图上挨着比较近的则节点的embeding比较相似,而没有关系的和不挨着的则embeding比较远 。
看到这里很多同学是不是有种比较熟悉的感觉,没错,这和前面文章 深入浅出理解word2vec模型 (理论与源码分析) 里介绍的 word2vec 原理极其相似,这种假设称为 同向偏好假设 ( 反之 就是 异向偏好,例如氨基酸更倾向于在不同类别之间建立起链接。这里暂不展开)。
我们 细看损失 会发现: 图上有监督学习是和标签比较计算出损失然后进行回传进行的训练。而图上无监督学习则是节点间彼此有链接的或关系较近的为正样本,没有链接的则基本上没有什么关系 ,通常的做法是直接进行 全局负采样得到。

(2) Link预测通俗理解
在说链接预测之前,我们需要对 图上跑深度学习算法 有一个 初步感知 ,并且默认正在阅读的同学是看过上面3篇历史文章的,这里说到的背景知识上述文章里都有。下面的内容要 敲小黑板了,注意了注意了~
我们知道: 图是由节点和边构建而成的空间结构,并且是非欧结构。在 GNN 或 GCN系列 的模型中,每个节点均有自己的Embeding , 而经过消息传递,每个节点把自己的信息沿着边Copy存入到邻居节点的 MailBox,然后每个节点均可以从自己的MailBox拿到邻居发送过来的Embeding ,然后依据某种方式进行自己Embedding 和 邻居节点的Embeding 进行聚合。这个真可以理解是“沿着网线来把信息传给你”~
一般采用的 聚合方式 通常是 Mean、Max 等方式, 同时,因为多个邻居信息构成一个 序列 ,则我们可以用Rnn、Lstm 等方式来进行聚合。更进一步,我们可以考虑 各节点自适应重要性 的Din Attention , Transform等方式来进行聚合。
我们可以自己选择使用 几跳的邻居 以及 训练全图几个Epoch 。其中在当前某一个Epoch中,每一跳邻居就相当于以当前种子节点为中心的 广度优先 遍历,从周围一圈中选取节点聚合到当前节点。而训练全图几个Epoch 则是在上一轮已经迭代更新过的每个节点的embeding上 再次做一遍 邻居聚合的过程。
从这我们可以看到: 拿到邻居信息来更新自身 ,在某种意义上可以让隔得比较近的节点更趋同,这个有好也有坏。
好处 是符合我们训练图模型的基础业务目标:学习出图中节点的关系,而这种关系的语义信息则包含在embeding 中。
但同时,缺点 就是:我们如果训练时候采集的邻居过多,或则全图更新训练的epoch过多,则会导致节点间区分能力不强,embedding 趋同,也就是过平滑问题。

更细节的说,训练一个链接预测模型涉及到比对种子节点和相连节点之间的得分以及种子节点与任意一个节点之间的得分的差异。例如,给定一条连接 𝑢 和 𝑣 的边,一个好的模型希望 𝑢 和 𝑣 之间的得分要高于 𝑢 和从一个任意的噪声分布 𝑣′∼𝑃𝑛(𝑣) 中所采样的节点 𝑣′ 之间的得分。其中从任意的噪声分布种选择邻居节点的方法称作 图数据的负采样。
链接预测虽然是无监督学习,但是其在现在很多互联网大厂中,用的是 极其广泛 的,我们仅仅需要根据用户行为日志构建好图即可,然后让模型自己去学习各种数据特征自身的结构关系,其产出的中间结果embedding 可以用于下游众多的业务与任务。
而本文介绍的代码也可以进行 文本语义的 相似性学习 ,例如:我们已经使用word2vec训练好了一个词典各个词语的embeding , 我们可以选择编辑距离断的词语构建边,然后来让模型去融合编辑距离限定的情况下词语间的语义关系,这何尝不是一种新的尝试呢。
在历史 graphSage还是HAN ?吐血力作综述Graph Embeding 经典好文 结尾中,我们推荐了 亚马逊的 DGL( Deep Graph Library ) 的 图深度学习框架,其中文官方文档完善而又通俗易懂,代码清晰且又容易理解,所以以后本系列基于图的文章的 核心代码 均基于DGL框架编写,下面让我们开始基于同构图的链接预测的代码时刻吧~
(3) 代码时光
看以前的读者留言说,历史文章的代码均集中在文章的最最后面,不利于阅读 ,很多时候代码看不懂的部分也没有注解。鉴于读者的背景知识与研究方向各异,以后我们改变一下文章的组织形式,理论结合代码穿插讲解 ,毕竟代码才是程序员表达自己思想的最好语言,不是吗? so , 让我们开始coding吧 ~
注意: 我们这里说明的代码是 基于dgl 和 graphsage来实现的同构图上的链接关系的预测 。
老规矩,开篇先吼一嗓子 , talk is cheap , show me the code !!!
(3.1) 导包
首先,我们导入本文中图深度学习所需要用的若干python包
import torch
import torch.nn as nn
import dgl
import dgl.nn.pytorch.conv as conv
import torch.nn as nn
import torch.nn.functional as F
import dgl.function as fn
import numpy as np
from dgl import save_graphs, load_graphs
其中,dgl是 基于pytorch开发 的 图深度学习框架,numpy作为我们初始的数据输入, conv为dgl实现的卷积核算子。 下面开始正式的代码讲解。
(3.2) 图定义和节点与边特征赋值
首先,要在图上进行链接预测任务,我们需要构建我们自己的逻辑图,这里采用dgl的图深度学习框架构建。我们要知道:在dgl框架中,构建图是以边的集合来进行图的定义的。具体如下所示:
src = np.random.randint(0, 100, 500)
dst = np.random.randint(0, 100, 500)
# 同时建立反向边
graph = dgl.graph((np.concatenate([src, dst]), np.concatenate([dst, src])))
print(graph)
# 图中节点的数量是DGL通过给定的图的边列表中最大的点ID推断所得出的
可以看到: 因为是基于边的集合进行图的构建,src则是边的起点,dst是边的终点。
注意: dgl的 最新版本 中,有向图与无向图以相同的定义方式定义。其中,有向图只用输入一个[src,dst]数据即可,而无向图则需要输入两组边的顶点数组,也可以使用 bgraph = dgl.to_bidirected(graph) 来实现同样的功能。
接着 ,在构造了好了图之后,我们也可以灵活的给节点和边添加特征以及标签数据。代码如下:
# 建立点和边特征,以及边的标签
graph.ndata['feature'] = torch.randn(100, 10)
graph.edata['feature'] = torch.randn(1000, 10)
graph.edata['label'] = torch.randn(1000) # 当然我们也可以给节点和边赋予一些特征。这里用不上,仅仅做为demo
这里的 graph.ndata 与graph.edata 则是分别给图的节点和边赋值的过程。
注意:节点和边内部的名称别重复 ,这里我们采用的方式得到的 embeding是不会随着网络训练而更新 的,在文章最后会介绍原因以及介绍可以随着网络更新的定义节点embeding特征的方法。
其中, 在 dgl框架 里,这里的特征的属性取值目前仅允许使用数值类型(如单精度浮点型、双精度浮点型和整型)的特征,这些特征可以是 标量、向量或多维张量 。

(3.3)模型结构定义
经过上面两步,图的逻辑结构已经有了,可以在图上跑我们的深度学习模型算法了。下面,让我们开始定义我们的模型结构吧~
@ 欢迎关注微信公众号:算法全栈之路
# coding:utf-8class SAGE(nn.Module):def __init__(self, in_feats, hid_feats, out_feats):super().__init__()# 实例化SAGEConv,这里调用官方sageconv算子in_feats是输入特征的维度,out_feats是输出特征的维度,aggregator_type是聚合函数的类型# 这个函数中完成了每个节点聚合邻居节点发送来的信息的过程,官方算子中间有多个全连接层参数是参与了模型训练的。起到不同节点聚合邻居的个性化的调节作用。self.conv1 = conv.SAGEConv(in_feats=in_feats, out_feats=hid_feats, aggregator_type='mean')self.conv2 = conv.SAGEConv(in_feats=hid_feats, out_feats=out_feats, aggregator_type='mean')def forward(self, graph, inputs):# 输入是节点的特征h = self.conv1(graph, inputs)h = F.relu(h)h = self.conv2(graph, h)return h# 下面是使用点积计算边得分的例子。
class DotProductPredictor(nn.Module):def forward(self, graph, h):# 这里是根据每条边的两个端点的隐藏向量的点积dot来计算边存在与否的score with graph.local_scope():graph.ndata['h'] = hgraph.apply_edges(fn.u_dot_v('h', 'h', 'score'))return graph.edata['score']class Model(nn.Module):def __init__(self, in_features, hidden_features, out_features):super().__init__()self.sage = SAGE(in_features, hidden_features, out_features)self.pred = DotProductPredictor()# 模型主题函数,调用sage子模型是2层的sageconv算子叠加的,然后得到sage子模块的输出隐藏向量。# 这里的隐藏向量已经涵盖有聚合邻居的信息了。然后分别将pos样本和neg样本输入pred模型得到两个打分。# 这里的g表示的是原生的逻辑图,我们自己构建起来的,而neg_g是对每个种子节点负采样后得到的子图。而在这里x是输入的所有节点的feature。def forward(self, g, neg_g, x):h = self.sage(g, x)# 注意这里多了一个返回,pos logit 和 neg logitreturn self.pred(g, h), self.pred(neg_g, h)注意这里,我们采用的是graphSage的方式来进行的链接预测。
首先这个 模型的骨架 是 model类定义的,其中调用了sage类和pred类。
对于sage类,sage类中又调用了2层官方的sageConv算子,在这个算子内部完成了每个节点聚合邻居节点发送来的信息的过程,官方算子中间有多个全连接层参数是参与了模型训练的,可以起到不同节点聚合邻居的个性化的调节作用。
对于pred类,我们观其大略应该知道,它其实是在算pos图和neg图的损失,然后让 pos图的打分接近1 ,然后neg图的打分接近0,以达到上面我们说的 同向偏好假设 所定义的损失关系。
(3.4) 模型负采样子图和损失函数
书接上文,我们可以看到 model类训练的时候需要输入 neg_g ,这个就是对 种子节点负采样 得到的子图。 这也符合我们上文强调过的无监督算法的主要意义:图上的无监督算法,事实存在的边就是正样本,而负样本是需要对每个种子正样本进行采样得到的。我们这里是采用的 随机采样 的方式。
如下面代码所示:
@ 欢迎关注微信公众号:算法全栈之路
# coding:utf-8# 涉及到对不存在的边的采样过程,负采样。因为上述的得分预测模型在图上进行计算,用户需要将负采样的样本表示为另外一个图,其中包含所有负采样的节点对作为边。
# 下面的例子展示了将负采样的样本表示为一个图。每一条边 (𝑢,𝑣) 都有 𝑘 个对应的负采样样本 (𝑢,𝑣𝑖),其中 𝑣𝑖 是从均匀分布中采样的。
def construct_negative_graph(graph, k):src, dst = graph.edges()neg_src = src.repeat_interleave(k)neg_dst = torch.randint(0, graph.num_nodes(), (len(src) * k,))return dgl.graph((neg_src, neg_dst), num_nodes=graph.num_nodes())我们可以看到,这里 K表示 每个正样本采样 几条边 作为负样本,并且 负边的起点依然是种子节点,只是终点端点是随机分布中采样 得到的。
另外,我们计算分别得到 pos图和neg图 的得分之后,需要计算最终的损失,我们这里没有采用有监督的交叉熵损失,而是采用了间隔损失。
# 间隔损失,训练的循环部分里会重复构建负采样图并计算损失函数值
def compute_loss(pos_score, neg_score):n_edges = pos_score.shape[0]return (1 - pos_score.unsqueeze(1) + neg_score.view(n_edges, -1)).clamp(min=0).mean()
间隔损失 的 核心思想也就是:让pos边打分越高越好,而让neg边打分越低越好。 因为最后我们是用梯度下降(Gradient Ddescent,GD)的算法来优往小的方向去优化loss, 所以在公式里我们可以看到加了 1 - pos_score 这一项,符合优化的基本原则。
注意:由于一个正样本对应多个负样本,这里调整了张量的shape,应用了张量的广播机制。

(3.5) 模型训练与 node embeding 导出
到这里,我们就可以开始模型的训练了。模型训练需要的的全局超参以及训练过程代码如下:
@ 欢迎关注微信公众号:算法全栈之路# 模型训练过程
node_features = graph.ndata['feature']
# 模型特征输入维度
n_features = node_features.shape[1]
# 负采样条数
k = 5
model = Model(n_features, 100, 8)
# 优化器
opt = torch.optim.Adam(model.parameters())for epoch in range(3):# 采样得到neg graph negative_graph = construct_negative_graph(graph, k) pos_score, neg_score = model(graph, negative_graph, node_features)# 计算损失loss = compute_loss(pos_score, neg_score)# 梯度优化opt.zero_grad()loss.backward()opt.step()print(loss.item())这里的代码逻辑很清晰并且代码很简单,我就不再赘述了。到这里,我们就可以成功的训练模型完成了。
最后一步,node embeding 导出。
因为我们是链接关系预测,真正线上使用的时候,我们需要拿到 两个节点的embeding进行点积计算链接概率 。因此,我们需要导出中间的embeding。 我们可以使用下面的方式导出节点的embedding ,并且输出第0个节点node 的embedding:
# 输出node embeding
# 训练后,节点表示可以通过以下代码获取。
node_embeddings = model.sage(graph, node_features)
print(node_embeddings[0])
训练过程与embedding导出 的终端输出结果如下:
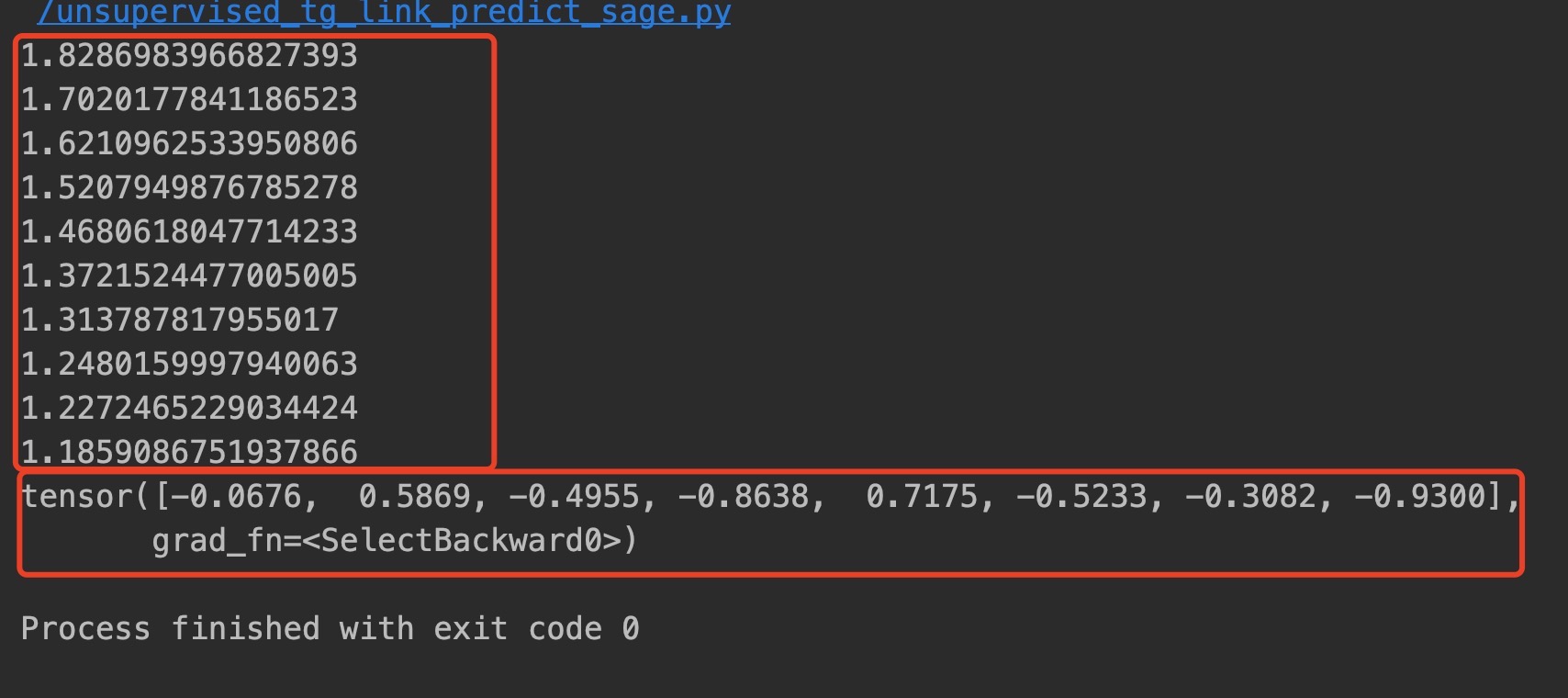
当然,我们也可以把图和模型保存下来,供以后重复使用。dgl 图 和 pytorch模型保存的代码如下:
from dgl import save_graphs, load_graphs
# 图数据和模型保存
save_graphs("graph.bin", [graph])
torch.save(model.state_dict(), "model.bin")the last last last , 这里面有一个很重要的细节就是: 代码里我们是基于外界输入的 随机生成的node feature 的embeding ,然后 使用GraphSage 的方法进行 邻居节点的聚合特性 的学习,可以平滑邻居节点的相似性。但是这里,模型仅仅起到平滑和融合邻居节点的作用,并 不会改变原始的node feature 的embeding 。 读者可以把各个node 的feature打印出来进行验证。所以在上文中,我们得到模型融合过邻居节点的隐藏表示的时候,是采用的 model.sage(graph, node_features) 的方式,这里输出的才是我们想要的embeding,因为它中间经过了 模型运算得到的隐藏层 信息。
如果我们希望模型可以直接 改变输入的node feature 的 embeding 并且 直接导出 就可以使用,让它也可以直接进行 链接关系Link 的predict 的话,我们创建 node feature 的时候,可以采用
embed=nn.Parameter(torch.Tensor(g.number_of_nodes, self.embed_size))
的方式来申明变量,
同时,让 优化器在定义优化 的时候,添加进来这一个部分的可训练参数,如下所示:
all_params = itertools.chain(model.parameters(), embed.parameters())
optimizer = torch.optim.Adam(all_params, lr=0.01, weight_decay=0)到这里,GraphSage实现同构图 Link 预测 ,通俗易懂好文强推 的全文就写完了。 上面的代码demo 在环境没问题的情况下,全部复制到一个python文件里,就可以完美运行起来。接下来会针对更详细的图上任务进行更多的源码说明~
写小作文 真是不容易,写代码果然是最容易的~。以前只是进行模型的使用,真正要去写文章的时候,太多的东西是源码上的过程,文字描述太难了! 哎,再接再厉吧,加深理解,加强文字的表达能力,go on !!!
宅男民工码字不易,你的关注是我持续输出的最大动力。
接下来作者会继续分享学习与工作中一些有用的、有意思的内容,点点手指头支持一下吧~
算法全栈之路
这篇关于GraphSage与DGL实现同构图 Link 预测,通俗易懂好文强推的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





