R语言实现医疗费用预测（数据科学导引）

【1】案例背景

保险公司通常需要募集比花费在受益者的医疗服务上更多的年度保费。因此，精确预测医疗费用对保险公司具有重要价值。

【2】方法陈述

观察变量间关系，建立线性回归模型，评估模型性能后进行改进，如添加非线性关系和考虑特征之间的相互影响等，得到改进的回归模型来进行预测。

【3】实验代码

1. 步骤一

读取数据，查看数据分布

insurance <- read.csv("C:/Users/17909/Desktop/insurance.csv")

#数据分布

s<-summary (as.factor(insurance$region))

as.data.frame(cbind(Number = names(s),Freq = s), row.names = 1:length(s))

summary(insurance)

2. 步骤二

建立相关系数矩阵，查看变量间关系。

#相关系数矩阵

mydata=insurance[,c(1,3,4,7)]

res=cor(mydata)

round(res,6)

#查看变量间关系

pairs(insurance[c("age", "bmi", "children", "charges")])

3. 步骤三

建立线性回归模型

#线性回归

ins_model <- lm(charges ~ age + children + bmi + sex + smoker + region, data=insurance)

ins_model

summary(ins_model)

4. 步骤四

添加非线性关系和特征间相互作用影响，改进模型。

#添加非线性关系

ins_new1_model <- lm(charges ~ .+age^2 , data=insurance)

ins_new1_model

summary(ins_new1_model)

#添加相互作用影响

insurance$bmi30 <- ifelse(insurance$bmi >= 30, 1, 0)

ins_new2_model<-lm(charges~.+age^2+bmi30:smoker,data = insurance)

ins_new2_model

summary(ins_new2_model)

【4】结果分析

由步骤一得数据分布如图1所示，发现数据几乎均匀地分布在4个地理区域中，医疗费用的分布不服从正态分布，需修正线性回归的假设。

图1 数据分布

由步骤二得各变量间的关联性不是强相关，但还是存在一定关联性（如图2所示）。age与charges并非呈现一元线性关系（如图3所示），与步骤一结论相吻合，因此，在做线性预测时，不能做简单的预测。

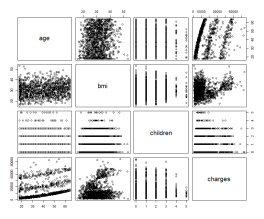图2 相关系数矩阵	图3 变量间关系

由步骤三可得线性回归结果如图4所示，R方值仅为0.7494，因此模型需要优化。

图4 简单线性回归模型

由步骤四得添加非线性因素后R方值变化并不明显（如图5所示），为0.7494，而添加肥胖属性后R方值提升到0.8268（如图6所示），因此优化可行。

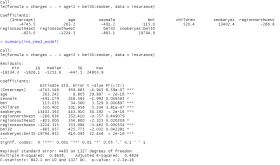图5 添加非线性因素后的模型	图6 添加肥胖属性后的模型