本文主要是介绍统计数字会撒谎,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1 常见统计场景
- 1.1 GPA越高越好吗?
- 1.2 我真的享受减税了吗?
- 1.3 到底多付了多少?
- 1.4 变好了还是变坏了?
- 1.5 物价涨了还是降了?
- 1.6 辍学率到底是多少?
- 1.7 收入增长的多吗?
- 1.8 军费增长的多吗?
- 2 对统计数据提出的五个问题
- 2.1 谁说的
- 2.2 如何知道的
- 2.3 样本是否足够大
- 2.4 是否遗漏了辅助信息
- 2.5 是否偷换了概念
- 3 辛普森悖论
- 3.1 解释
- 3.2 扩展
- 3.3 应用
1 常见统计场景
1.1 GPA越高越好吗?
GPA,平均成绩点数,是计算大学学业的表现方法,通俗点说就是学生在校的平均成绩
计算方法如下:
1、 百分制折算为等级成绩,等级成绩换算为分值
| 分数 | 等级 | 分值 |
|---|---|---|
| 90-100 | A | 4 |
| 80-90 | B | 3 |
| 70-80 | C | 2 |
| 60-70 | D | 1 |
2、 单科绩点=分值*学分
3、 GPA=总绩点/总学分=所有科的绩点之和/所有科的学分之和
GPA是评价学术潜力的一个方便快捷的指标,一个GPA3.5的学生显然要比另一个GPA2.5的学生的实力强,GPA不仅计算容易、理解容易,而且对不同学生进行比较也很容易
但是这个指标是完美的吗?
总结:GPA没有反映不同学生所选课程的难易程度,假设一个GPA为3.5的学生选的都是容易的课,而GPA2.9的学生的课程表里尽是微积分、物理这类难学的课,我们能一口判定孰优孰劣吗?
描述统计学的意义就是简化,但过于简化会不可避免地丢失一些内容和细节。
1.2 我真的享受减税了吗?
政府要推行一个新的减税政策,这一政策将惠及绝大多数家庭,在这项政策推行后,将会有1亿人享受减税待遇,人均减税额超过1000元。
从数字上看,直观的认为大部分人都能减税1000元左右,但是如果减税中位数是100元呢?
总结:从准确性角度看,平均数和中位数取哪个,关键在用这个数据分布里的异常值对事实的真相是起到扭曲作用,还是其重要的组成部分。判断比统计更重要。
1.3 到底多付了多少?
百分差和百分率的区别
北京市的个人所得税税率由原来的3%上调到5%
有两种描述方法:
个人所得税税率上升了2个百分点,从3%涨到5%
个人所得税税率上升了67%
总结:这两种描述方法都没有问题,只是所站角度不同
1.4 变好了还是变坏了?
教育水平是变好了还是变坏了
政客甲(挑战者):我们的教育水平正变得原来越糟!2013年有6成学校的考试成绩低于2012年
政客乙(在任者):我么的教育水平正变得越来越好!2013年有8成学生的考试成绩高于2012年
从上述数据,我们并不能简单的说变化还是变坏,只能得到下述信息:
1 学校的规模差距比较大;
2 成绩上升的学生大部分来自于规模较大的学校;
3 成绩下降的学生大部分来自于规模较小的学校。
经济变好了还是变坏了
政客甲(平民主义者):我们的经济一塌糊涂!2012年有30个州的收入都出现了下滑
政客乙(更接近精英派):我们的经纪走势一片光明!2012年有70%的美国人的收入增加了
从上述数据,我们能得到下述信息:
1 州的规模差距较大;
2 收入上升的州可能是规模较大的州;
3 收入下滑的州可能是规模较小的州。
总结:要明确分析的目的,分清分析的单位,描述的对象到底是谁(或什么),以及不同的人口中的谁(或什么)是不是存在差异
1.5 物价涨了还是降了?
举一个简单的例子,假设去年一夸脱牛奶值 20 美分,一条面包 5 美分。今年牛奶的价格降至 10 美分,而面包的价格升至 l0 美分。现在你想证明什么呢? 物价指数上升?
物价指数下降?或者根本没有变化?
方法1:以去年为基期
牛奶的价格降了50% (10-20)/20
面包的价格涨了100% (10-5)/5
即今年涨了25% (-50%+100%)/2=25%
方法2:以今年为基期
去年牛奶的价格高于今年的100% (20-10)/10
面包的价格低于今年的50% (5-10)/10
即今年降了25%(-100%+50%)/2=25%
方法3:几何平均数(若有N个数,则这N个数的积开N次方就是N个数的几何平均数)
以去年为基期为例,
去年每种商品的价格都看成 100%,将两个 100%相乘再开平方根,得到 100%,这是去年价格指数的几何平均数
今年牛奶是去年的50%,面包是去年的 200%,50%乘以 200%得10000%,再开平方根得100%
价格没升没降
1.6 辍学率到底是多少?
某市教育局公布的高中辍学率为1.5%,而某电视栏目组暗访计算的辍学率为25%~50%
原因:教育局认为转学、出国或攻读一般同等学力的不是辍学,不纳入统计
2023年5月中国青年(16-24岁)失业率高达20.8%,真实的失业率到底是多少?
国家统计局的统计口径:将16岁及以上人口划分成三类,一类是就业,一类是失业,还有一类是非劳动力。按照国际劳工组织的标准,就业人口是指在调查参考期内,通常为一周,为了取得劳动报酬或经营收入而工作一小时及以上和因休假、临时停工等暂时离岗的人,这些人都属于就业
失业率=1-(一周内工作一小时及以上的人/(就业的人+失业的人))
1.7 收入增长的多吗?
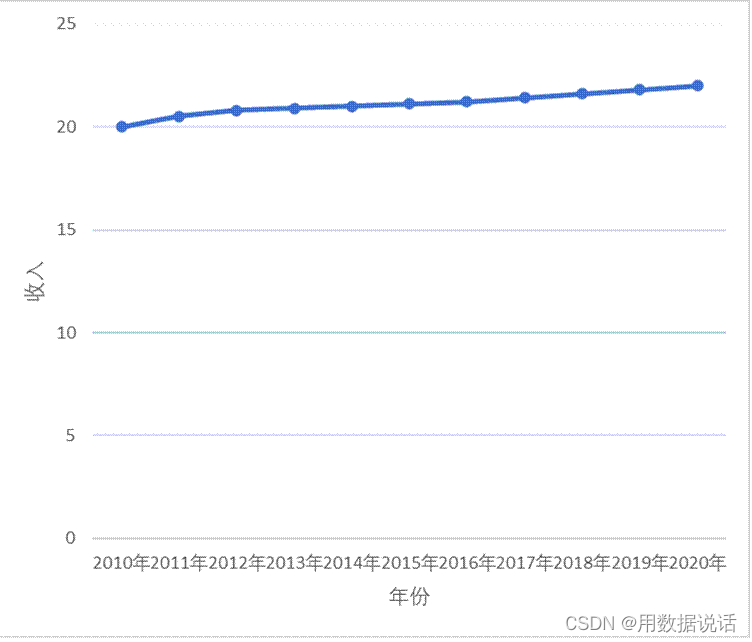
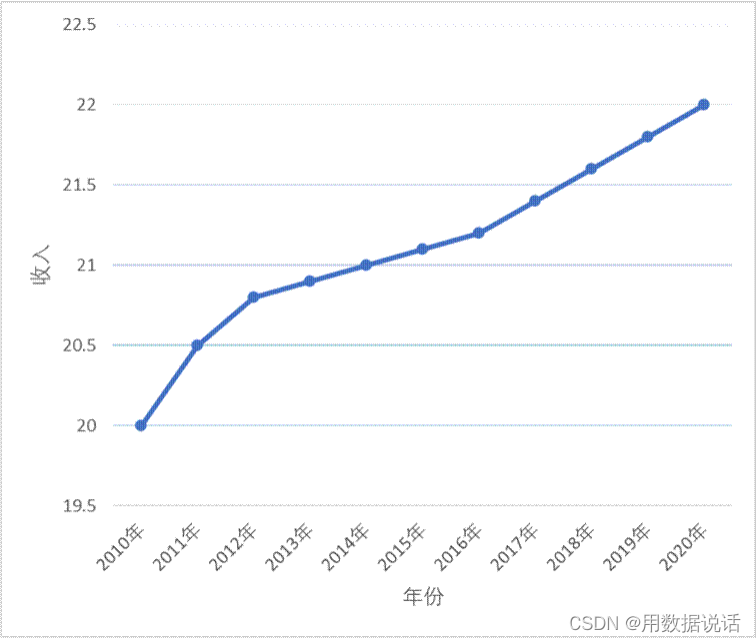
总结:同一套数据,图表的刻度不同,给人的印象也不一样
1.8 军费增长的多吗?
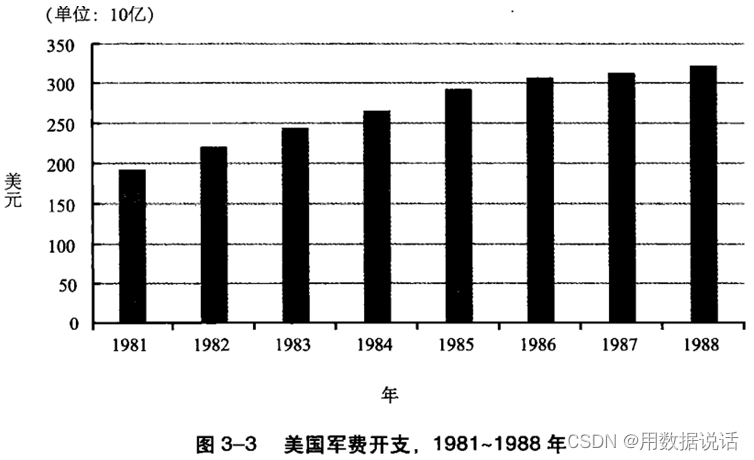
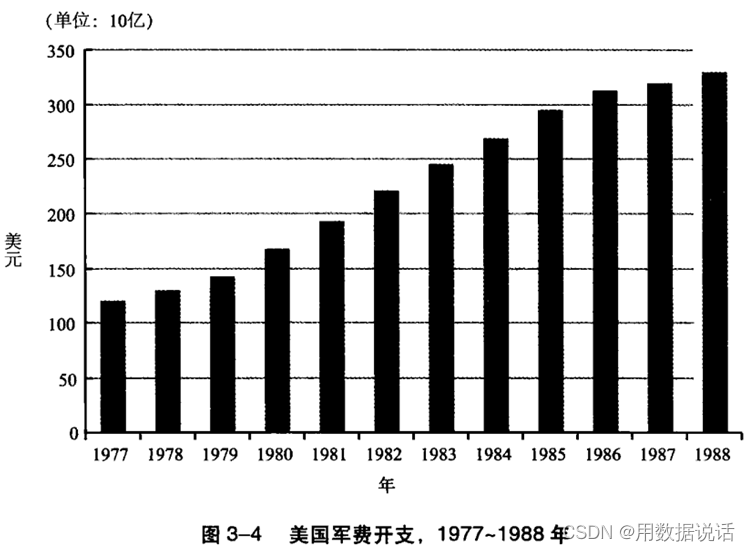
总结:同一套数据,选择的时间范围不一样,给人的印象也不一样
2 对统计数据提出的五个问题
2.1 谁说的
首先要寻找的是偏差——出于学说、名誉或收入的考虑而需要证明某些结论的实验室,希望获得一篇好报道的报界,工资已岌岌可危的工人和管理部门都有可能制造偏差。
有意识的偏差:刻意舍弃部分数据;改变测量标准
无意识偏差:幸存者偏差
谨防“专家”“权威人士”
2.2 如何知道的
谨防有偏抽样,是选择不当还是刻意挑选有利的样本
2.3 样本是否足够大
谨防样本量过小、以偏概全“沉默的大多数”
2.4 是否遗漏了辅助信息
一项研究表明,在 2800 个案例中,超过半数的患者母亲年龄是 35 岁或超过 35 岁;
在大雾的一周内,伦敦市郊的死亡人数猛增至 2800 人;
约翰斯·霍普金斯大学 1/3 的女学生嫁给了大学老师;
2.5 是否偷换了概念
谨防统计口径的变化
某国某个地区的人口总数是2800万,5年后这个数据 却变成了10500万,当中只有小部分的增长是真实的。
产生前后两次巨大差异的原因可归结为不同的调查目的,第一次是为征税和征兵服务的,第二次却是为了发放救济粮。
3 辛普森悖论
3.1 解释
谁的命中率更好?
先看第一场比赛:
| 运动员 | 两分球命中率 | 三分球命中率 |
|---|---|---|
| 詹姆斯 | 52.94% | 41.67% |
| 库里 | 57.14% | 53.85% |
其中:
两分球命中率 = 两分球命中数 / 两分球出手数 * 100%
三分球命中率 = 三分球命中数 / 三分球出手数 * 100%
总命中率 = (两分球命中数 + 三分球命中数) / (两分球出手数 + 三分球出手数) * 100%
看一下明细数据
| 运动员 | 两份球命中数 | 两分球出手数 | 两分球命中率 | 三分球命中数 | 三分球出手数 | 三分球命中率 | 总命中数 | 总出手数 | 总命中率 |
|---|---|---|---|---|---|---|---|---|---|
| 詹姆斯 | 9 | 17 | 52.94% | 5 | 12 | 41.67% | 14 | 29 | 48.28% |
| 库里 | 8 | 14 | 57.14% | 7 | 13 | 53.85% | 15 | 27 | 55.56% |
再来看另一场比赛:
| 运动员 | 两分球命中率 | 三分球命中率 |
|---|---|---|
| 詹姆斯 | 55.00% | 33.33% |
| 库里 | 57.14% | 47.06% |
再来看一下明细数据
| 运动员 | 两份球命中数 | 两分球出手数 | 两分球命中率 | 三分球命中数 | 三分球出手数 | 三分球命中率 | 总命中数 | 总出手数 | 总命中率 |
|---|---|---|---|---|---|---|---|---|---|
| 詹姆斯 | 11 | 20 | 55.00% | 1 | 3 | 33.33% | 12 | 23 | 52.17% |
| 库里 | 4 | 7 | 57.14% | 8 | 17 | 47.06% | 12 | 24 | 50.00% |
詹姆斯的两分球命中率也低于库里,三分球命中率也低于库里,但是汇总起来看,詹姆斯的投篮命中率是要高于库里的!
百科上对辛普森悖论的解释:
计算分项的比例(比如各种各样的率)数据时,A的每一分项的数据都比B要高,但是把各分项一汇总起来算总体数据时,A却比B低。这种不符合常规认知的“悖论”现象,在数据分析领域并不少见;这种在进行分组研究的时候,有时在每个组比较时都占优势的一方,在总评中有时反而是失势的一方的“悖论”现象就叫辛普森悖论。
在数学上的解释:

詹姆斯的投篮主要来自于两分球,三分球投的少(总投篮命中率主要由其两分球命中率主导)
库里的投篮主要来自于三分球,两分球投的少(总投篮命中率主要由其三分球命中率主导)
而三分球的命中率天然就会比两份球低得多,尽管库里三分球命中率远高于詹姆斯的三分球命中率,但再高也没有詹姆斯的两分球命中率高。
3.2 扩展
在真实的数据分析工作中,真实的数据形态往往更复杂,更多样,而标准的辛普森悖论也有很多的扩展甚至是变种的形态。根据数据分析经验总结起来,辛普森悖论更多的时候是从总体拆分到细项维度的时候发现的,而触发辛普森悖论,就是因为你选择了这个维度做拆分。所以,在数据分析中,对决策危害最大的错误就是:在分析的时候遗漏了关键的维度;而触发辛普森悖论的维度,恰恰是最不应该遗漏的!
所以,辛普森悖论的扩展定义可以归纳为:在增加了维度后使得数据结论反转的现象,均可称为是辛普森悖论现象
3.3 应用
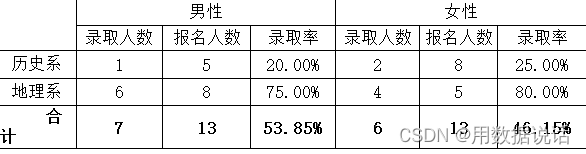
尽管每个系女生的录取率都更高,但整体算下来男生的录取率却更高
地理系 8名男性报名(8/13=61.5%),录取了6人(6/8=75%)
历史系 8名女性报名(8/13=61.5%),录取了2人(2/8=25%
这篇关于统计数字会撒谎的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


