【递归】(三) (Memorization) 记忆化技术

2023-10-14 13:10
文章标签 技术 递归 记忆 memorization

本文主要是介绍【递归】(三) (Memorization) 记忆化技术，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

一、递归中的重复计算

二、斐波那契数

2.1 题目要求

2.2 解决过程

三、爬楼梯

3.1 题目要求

3.2 解决过程

四、爬楼梯多解

一、递归中的重复计算

# Python implementation
def fibonacci(n):""":type n: int:rtype: int"""if n < 2:return nelse:return fibonacci(n-1) + fibonacci(n-2)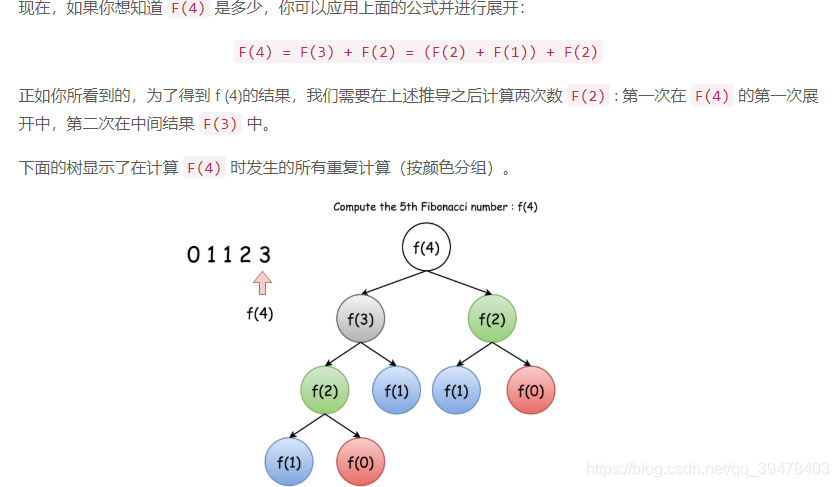

def fib(self, N):""":type N: int:rtype: int"""cache = {}def recur_fib(N):if N in cache:return cache[N]if N < 2:result = Nelse:result = recur_fib(N-1) + recur_fib(N-2)# put result in cache for later reference.cache[N] = resultreturn resultreturn recur_fib(N)

参考文献：https://leetcode-cn.com/explore/orignial/card/recursion-i/258/memorization/1211/

二、斐波那契数

2.1 题目要求

2.2 解决过程

个人实现

法一：无记忆递归。

2020/07/19 - 18.27% (800ms) - 最简单但低效的方法 

class Solution:def fib(self, N: int) -> int:if N == 1:return 1if N == 0:return 0return self.fib(N-1) + self.fib(N-2)

法二：有记忆递归。使用字典 memory 来记忆计算过的结果，避免重复冗余的计算。

2020/07/19 - 53.74% (44ms) - 性能显著提升，但由于实现存在问题，未能发挥最佳效果 (对比官方法三)

class Solution:def __init__(self):self.memory = {0: 0, 1: 1}  # 计算记录, 但其实这种方式效率并不高, 详见官方法三def fib(self, N: int) -> int:if N in self.memory:return self.memory[N]else:self.memory[N] = self.fib(N-1) + self.fib(N-2)  # 记忆return self.memory[N]

官方实现与说明

class Solution:def fib(self, N: int) -> int:if N <= 1:return Nreturn self.fib(N-1) + self.fib(N-2)

2020/07/19 - 12.98% (800ms)

class Solution:def fib(self, N: int) -> int:if N <= 1:return Nreturn self.memoize(N)def memoize(self, N: int) -> {}:cache = {0: 0, 1: 1}# Since range is exclusive and we want to include N, we need to put N+1.for i in range(2, N+1):cache[i] = cache[i-1] + cache[i-2]return cache[N]

2020/07/19 - 73.37% (40ms)

## 这比个人实现二还要好, 注意对比 cache 的来源与差异
class Solution:def fib(self, N: int) -> int:if N <= 1:return Nself.cache = {0: 0, 1: 1}  # 比放在数据成员的个人实现法二要好return self.memoize(N)def memoize(self, N: int) -> {}:if N in self.cache:return self.cache[N]self.cache[N] = self.memoize(N-1) + self.memoize(N-2)return self.memoize(N)

 2020/07/19 - 99.21% (28ms) - 接近最佳 (注意，实现时将递归体封装在另一个成员函数中了)

class Solution:def fib(self, N: int) -> int:if (N <= 1):return Nif (N == 2):return 1current = 0prev1 = 1prev2 = 1# Since range is exclusive and we want to include N, we need to put N+1.for i in range(3, N+1):current = prev1 + prev2prev2 = prev1prev1 = currentreturn current

2020/07/19 - 53.74% (44ms)

## 这就牛掰了, 开始使用数学思想了, 所以更有些费解, 但很值得学习！
class Solution:def fib(self, N: int) -> int:if (N <= 1):return NA = [[1, 1], [1, 0]]  # 中间幂矩阵的基数矩阵self.matrix_power(A, N-1)  # 使用递归函数 matrixPower 计算给定矩阵 A 的幂。幂为 N-1return A[0][0]def matrix_power(self, A: list, N: int):if (N <= 1):return Aself.matrix_power(A, N//2)  # matrixPower 函数将对 N/2 个斐波那契数进行操作！self.multiply(A, A)  # 矩阵乘法B = [[1, 1], [1, 0]]if (N%2 != 0):  # 奇数次补乘 如 3, 因为对于偶数次幂 N=2x 而奇数次幂 N=2x+1self.multiply(A, B)def multiply(self, A: list, B: list):x = A[0][0] * B[0][0] + A[0][1] * B[1][0]y = A[0][0] * B[0][1] + A[0][1] * B[1][1]z = A[1][0] * B[0][0] + A[1][1] * B[1][0]w = A[1][0] * B[0][1] + A[1][1] * B[1][1]A[0][0] = xA[0][1] = yA[1][0] = zA[1][1] = w

2020/07/19 - 96.20% (32ms) - 接近最佳，强大的 O(logn) 复杂度

# 这是什么神仙操作 ...
class Solution:def fib(self, N):golden_ratio = (1 + 5 ** 0.5) / 2return int((golden_ratio ** N + 1) / 5 ** 0.5)

2020/07/19 - 96.20% (32ms) - 最佳，惊人的 O(1) 复杂度

其他实现 

若此时要求 通过递归返回斐波那契数列的前 N 项，则出了有记忆递归，还可以：

LRU cache 缓存装饰器 (decorator)：根据参数缓存每次函数调用结果，对于相同参数的，无需重新函数计算，直接返回之前缓存的返回值。缓存数据是并不一定快，要综合考量缓存的代价以及缓存的时效大小。经典例子是改造 fib 序列。

  • 若 maxsize=None，则禁用 LRU 功能，且缓存可无限制增长；当 maxsize=2^x 时，LRU 功能执行得最好；
  • 若 typed=True，则不同类型的函数参数将单独缓存。例如，f(2) 和 f(2.0) 将被视为具有不同结果的不同调用；
  • 缓存是有内存存储空间限制的；

2020/07/20 - 73.37% (40ms) - 不错

from functools import lru_cache
class Solution:@lru_cachedef fib(self, N: int) -> int:if N <= 1:return Nreturn self.fib(N-1) + self.fib(N-2)

参考文献

https://leetcode-cn.com/explore/orignial/card/recursion-i/258/memorization/1212/

https://leetcode-cn.com/problems/fibonacci-number/solution/fei-bo-na-qi-shu-by-leetcode/

https://www.jianshu.com/p/1e8318220bba

https://mp.weixin.qq.com/s?__biz=MzU0MDczMDUzMQ==&mid=2247484006&idx=1&sn=04d79d1ac51eabec5dfe2f3f444abff6&chksm=fb35f7aacc427ebccfaeb9faf55a9240d5e0dd35a8d4c1b0eff37637ef0243b30ccbe4b5da7d&scene=158#rd

三、爬楼梯

3.1 题目要求

3.2 解决过程

个人实现

法一：数学法 - 组合。通过排列组合中的 组合公式，累计 1 和 2 元素的各组合数。对本题而言，不论是爬一大步还是爬一小步，只要是爬 1 阶，就都是 无差别的，2 阶同理。故此处使用组合而非排列，通过 m！消除重复的排列情况。空间复杂度 O(1)，时间复杂度 O(n^2) ？

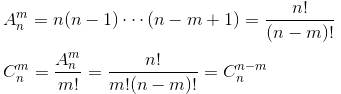
此外，该实现的高效性得益于 math.factorial() 函数的底层优化，否则手写阶乘函数效率将会极其低下。

2020/07/21 - 98.95% (28ms) - 数学法往往效果很好

class Solution:def climbStairs(self, n: int) -> int:if n < 4:return none = n                     # 初始化 n 个 1two = 0                     # 初始化 0 个 2limit = n // 2              # 2 个数上限count = 0                   # 种类计数while two <= limit:# 数据准备summ = one + two        # nminn = min(one, two)    # mdiff = summ - minn      # n-m# 组合 C^m_n = A^m_n / m! = n! / (n-m)! / m!count += (math.factorial(summ) // math.factorial(diff)) // math.factorial(minn)  # 更新组合元素 one -= 2                # 减少 2 个 1two += 1                # 增加 1 个 2return count

法二：数学法 - 找规律。根据测试用例及其结果，可以发现如下数列规律：

  • 输入：1、2、3、4、5、6、7 ...
  • 输出：1、2、3、5、8、13、21 ...

即从第三个数字开始，每个数字都是前两个数字之和，这就是 斐波那契数列 的性质，因此可以直接使用斐波那契数的解法来处理本题。

2020/07/22 - 15.86% (48ms) - 实现相对低效

class Solution:def climbStairs(self, n: int) -> int:if n < 4:return nself.cache = {1: 1, 2: 2, 3: 3}return self.fib(n)def fib(self, m):if m in self.cache:return self.cache[m]self.cache[m] = self.fib(m-1) + self.fib(m-2)return self.cache[m]

法三：数学法 - 黄金分割比。修改自上一题 —— 斐波那契数的官方实现六。空间复杂度 O(1)，时间复杂度 O(1)。

2020/07/22 - 85.31% (36ms) - 强大

class Solution:def climbStairs(self, n: int) -> int:if n < 4:return ngolden_ratio = (1 + 5 ** 0.5) / 2return int((golden_ratio ** (n+1) + 1) / 5 ** 0.5)  # n 改成 n+1

官方实现与说明

个人理解：因为第 x-1 阶与第 x-2 阶有别，故各自的攀爬方案 f(x-1) 与 f(x-2) 一定完全不同。而要想一次爬到第 x 阶，只有两种初始情况：从第 x-1 阶爬 1 步 or 从第 x-2 阶爬 2 步。故第 x 阶的攀爬方案满足 f(x) = f(x-1) + f(x-2)。

// C++ implementation
class Solution {
public:int climbStairs(int n) {int p = 0, q = 0, r = 1;for (int i = 1; i <= n; ++i) {p = q; q = r; r = p + q;}return r;}
};

// JAVA implementation
class Solution {public int climbStairs(int n) {int p = 0, q = 0, r = 1;for (int i = 1; i <= n; ++i) {p = q; q = r; r = p + q;}return r;}
}

// JAVA implementation
public class Solution {public int climbStairs(int n) {int[][] q = {{1, 1}, {1, 0}};int[][] res = pow(q, n);return res[0][0];}public int[][] pow(int[][] a, int n) {int[][] ret = {{1, 0}, {0, 1}};while (n > 0) {if ((n & 1) == 1) {ret = multiply(ret, a);}n >>= 1;a = multiply(a, a);}return ret;}public int[][] multiply(int[][] a, int[][] b) {int[][] c = new int[2][2];for (int i = 0; i < 2; i++) {for (int j = 0; j < 2; j++) {c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];}}return c;}
}

 

// JAVA implementation
public class Solution {public int climbStairs(int n) {double sqrt5 = Math.sqrt(5);double fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);return (int)(fibn / sqrt5);}
}
# Python implementation
class Solution:def climbStairs(self, n: int) -> int:if n < 4:return nsqrt5 = math.sqrt(5)fibn = math.pow((1+sqrt5) / 2, n+1) - math.pow((1-sqrt5) / 2, n+1)return int(fibn / sqrt5)

参考文献

https://leetcode-cn.com/explore/orignial/card/recursion-i/258/memorization/1213/

https://leetcode-cn.com/problems/climbing-stairs/solution/pa-lou-ti-by-leetcode-solution/

四、爬楼梯

// JAVA implementation
public class Solution {public int climbStairs(int n) {climb_Stairs(0, n);}public int climb_Stairs(int i, int n) {if (i > n) {return 0;}if (i == n) {return 1;}return climb_Stairs(i + 1, n) + climb_Stairs(i + 2, n);}
}
# Python implementation
class Solution:def climbStairs(self, n: int) -> int:return self.climb_Stairs(0, n)def climb_Stairs(self, i, n):if i > n:return 0if i == n:return 1return self.climb_Stairs(i+1, n) + self.climb_Stairs(i+2, n)

// JAVA implementation
public class Solution {public int climbStairs(int n) {int memo[] = new int[n + 1];return climb_Stairs(0, n, memo);}public int climb_Stairs(int i, int n, int memo[]) {if (i > n) {return 0;}if (i == n) {return 1;}if (memo[i] > 0) {return memo[i];}memo[i] = climb_Stairs(i + 1, n, memo) + climb_Stairs(i + 2, n, memo);return memo[i];}
}
# Python implementation
class Solution:def climbStairs(self, n: int) -> int:memo = [0 for _ in range(n+1)]  # memo = [0] * (n+1)return self.climb_Stairs(0, n, memo)def climb_Stairs(self, i, n, memo):if i > n:return 0if i == n:return 1if memo[i] > 0:return memo[i]memo[i] = self.climb_Stairs(i+1, n, memo) + self.climb_Stairs(i+2, n, memo)return memo[i]

// JAVA implementation
public class Solution {public int climbStairs(int n) {if (n == 1) {return 1;}int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}

// JAVA implementation
public class Solution {public int climbStairs(int n) {if (n == 1) {return 1;}int first = 1;int second = 2;for (int i = 3; i <= n; i++) {int third = first + second;first = second;second = third;}return second;}
}

// JAVA implementationpublic class Solution {public int climbStairs(int n) {int[][] q = {{1, 1}, {1, 0}};int[][] res = pow(q, n);return res[0][0];}public int[][] pow(int[][] a, int n) {int[][] ret = {{1, 0}, {0, 1}};while (n > 0) {if ((n & 1) == 1) {ret = multiply(ret, a);}n >>= 1;a = multiply(a, a);}return ret;}public int[][] multiply(int[][] a, int[][] b) {int[][] c = new int[2][2];for (int i = 0; i < 2; i++) {for (int j = 0; j < 2; j++) {c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];}}return c;}
}

// JAVA implementation
public class Solution {public int climbStairs(int n) {double sqrt5=Math.sqrt(5);double fibn=Math.pow((1+sqrt5)/2,n+1)-Math.pow((1-sqrt5)/2,n+1);return (int)(fibn/sqrt5);}
}

 参考文献：https://leetcode-cn.com/explore/orignial/card/recursion-i/258/memorization/1214/#3

这篇关于【递归】(三) (Memorization) 记忆化技术的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/210722。

相关文章

Qt如何实现文本编辑器光标高亮技术

Qt如何实现文本编辑器光标高亮技术

《Qt如何实现文本编辑器光标高亮技术》这篇文章主要为大家详细介绍了Qt如何实现文本编辑器光标高亮技术,文中的示例代码讲解详细,具有一定的借鉴价值,有需要的小伙伴可以了解下... 目录实现代码函数作用概述代码详解 + 注释使用 QTextEdit 的高亮技术（重点）总结用到的关键技术点应用场景举例示例优化建议
阅读更多...
Java中的登录技术保姆级详细教程

Java中的登录技术保姆级详细教程

《Java中的登录技术保姆级详细教程》：本文主要介绍Java中登录技术保姆级详细教程的相关资料,在Java中我们可以使用各种技术和框架来实现这些功能,文中通过代码介绍的非常详细,需要的朋友可以参考... 目录1.登录思路2.登录标记1.会话技术2.会话跟踪1.Cookie技术2.Session技术3.令牌技
阅读更多...
Web技术与Nginx网站环境部署教程

Web技术与Nginx网站环境部署教程

《Web技术与Nginx网站环境部署教程》：本文主要介绍Web技术与Nginx网站环境部署教程,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录一、Web基础1.域名系统DNS2.Hosts文件3.DNS4.域名注册二.网页与html1.网页概述2.HTML概述3.
阅读更多...
Java使用WebView实现桌面程序的技术指南

Java使用WebView实现桌面程序的技术指南

《Java使用WebView实现桌面程序的技术指南》在现代软件开发中,许多应用需要在桌面程序中嵌入Web页面,例如,你可能需要在Java桌面应用中嵌入一部分Web前端,或者加载一个HTML5界面以增强... 目录1、简述2、WebView 特点3、搭建 WebView 示例3.1 添加 JavaFX 依赖3
阅读更多...
mysql递归查询语法WITH RECURSIVE的使用

mysql递归查询语法WITH RECURSIVE的使用

《mysql递归查询语法WITHRECURSIVE的使用》本文主要介绍了mysql递归查询语法WITHRECURSIVE的使用,WITHRECURSIVE用于执行递归查询,特别适合处理层级结构或递归... 目录基本语法结构：关键部分解析：递归查询的工作流程：示例：员工与经理的层级关系解释：示例：树形结构的数
阅读更多...
C语言函数递归实际应用举例详解

C语言函数递归实际应用举例详解

《C语言函数递归实际应用举例详解》程序调用自身的编程技巧称为递归,递归做为一种算法在程序设计语言中广泛应用,：本文主要介绍C语言函数递归实际应用举例的相关资料,文中通过代码介绍的非常详细,需要的朋... 目录前言一、递归的概念与思想二、递归的限制条件 三、递归的实际应用举例（一）求 n 的阶乘（二）顺序打印
阅读更多...
SpringBoot3实现Gzip压缩优化的技术指南

SpringBoot3实现Gzip压缩优化的技术指南

《SpringBoot3实现Gzip压缩优化的技术指南》随着Web应用的用户量和数据量增加,网络带宽和页面加载速度逐渐成为瓶颈,为了减少数据传输量,提高用户体验,我们可以使用Gzip压缩HTTP响应,... 目录1、简述2、配置2.1 添加依赖2.2 配置 Gzip 压缩3、服务端应用4、前端应用4.1 N
阅读更多...
Java利用JSONPath操作JSON数据的技术指南

Java利用JSONPath操作JSON数据的技术指南

《Java利用JSONPath操作JSON数据的技术指南》JSONPath是一种强大的工具,用于查询和操作JSON数据,类似于SQL的语法,它为处理复杂的JSON数据结构提供了简单且高效... 目录1、简述2、什么是 jsONPath？3、Java 示例3.1 基本查询3.2 过滤查询3.3 递归搜索3.4
阅读更多...
Python中随机休眠技术原理与应用详解

Python中随机休眠技术原理与应用详解

《Python中随机休眠技术原理与应用详解》在编程中,让程序暂停执行特定时间是常见需求,当需要引入不确定性时,随机休眠就成为关键技巧,下面我们就来看看Python中随机休眠技术的具体实现与应用吧... 目录引言一、实现原理与基础方法1.1 核心函数解析1.2 基础实现模板1.3 整数版实现二、典型应用场景2
阅读更多...
Jackson库进行JSON 序列化时遇到了无限递归(Infinite Recursion)的问题及解决方案

Jackson库进行JSON 序列化时遇到了无限递归(Infinite Recursion)的问题及解决方案

《Jackson库进行JSON序列化时遇到了无限递归(InfiniteRecursion)的问题及解决方案》使用Jackson库进行JSON序列化时遇到了无限递归(InfiniteRecursi... 目录解决方案‌1. 使用 @jsonIgnore 忽略一个方向的引用2. 使用 @JsonManagedR
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2