九宫重排（隐式图搜索问题）

实验要求

1）对九宫重排问题，建立图的启发式搜索求解方法；
2）用A*算法求解九宫重排问题。

实验设计

3х3九宫棋盘，放置数码为1~8的8个棋子，棋盘中留有一个空格，空格周围的棋子可以移动到空格中，从
而改变棋盘的布局。根据给定初始布局和目标布局，移动棋子从初始布局到达目标布局，求解移动步骤并
输出。请设计算法，使用合适的搜索策略，在较少的空间和时间代价下找到最短路径。

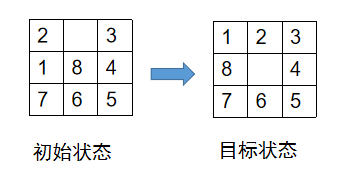
实验分析

① 从题目中可以看到 “开始状态” 和 “目标状态” 的字眼，并且从一个状态转移到另外的一个状态需要执行一次操作，最终需要求解的是从一个状态转移到另外一个状态需要执行的最少次数，这些都是BFS能够解决问题的典型特征，所以我们可以使用BFS来进行解决，这道题目也类似于走出迷宫的最少步数的问题，除了使用BFS来进行，对于这种可能性不太确定的问题，我们还可以使用深度优先搜索来进行解决，但是使用深搜解决时间复杂度可能更高。

② A算法解决这个问题，我们首先应该确定估价函数h(x)，估价函数的选取直接决定A算法的效率，一般对于八数码问题有三种估价函数的选法：

1. 以不在位的数码的个数为估价函数

2. 以不在位的数码归位所需的最短距离和即曼哈顿距离为估价函数

3. 将逆序对数作为估价函数

可以证明前两种都是乐观估计，最后一种不是，因此前两种都可以作为八数码问题的估价函数，但是你的估计值与真实值越近所需要搜索的状态越少，很明显第一种方法太乐观了（估价函数的选取直接决定算法的效率），因此我们采用第二种方法作为八数码问题的估价函数

解决了估价函数的问题以后，第二个需要解决的问题就是判重，我们首先想到的是用集合set，这种方法最简单，但是很不幸这种方法耗时也是最多的，如果时间要求比较高的话，这种情况很容易超时。这里我们不用这种方法，判重问题自然而然想到的是哈希表，好了现在问题又来了，如何创建哈希表，也就是哈希函数怎么写，这个东西比较有技巧，还好对于这种问题有一种现成的方法解决，那就是康托展开 ，还有一个问题就是有些问题是无解的，这种情况我们不希望进行很大力气的搜索之后发现无解，最好是能提前预知，值得庆幸的是八数码无论怎么移动逆序的奇偶性不变，因此我们可以直接通过O（1）的时间判断开始和目标结点的逆序奇偶性是否相同就可以了。有了上面的分析之后，程序就可以写出来了。
代码链接待加…