LBP纹理特征整理 文献阅读整理

LBP纹理特征

《Multiresolution gray-scale and rotation invariant texture classification with local binary patterns》文献阅读整理

前言

局部二值模式(Local Binary Pattern, LBP)是一种用来描述图像局部纹理特征的算法，反映的是图像像素点周围纹理变化情况，具有旋转不变性、灰度不变性（光照变化无影响）、计算复杂度低等优点。1994年首次由Timo Ojala, Matti Pietikainen等人提出，广泛应用于图像分析领域。

原始LBP特征

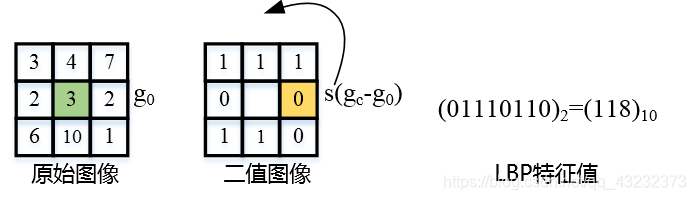
LBP特征提取图示： a）中红色部分为中心像素值。

总结后的计算过程如下：

1） 输入图像若为彩色图像，则将其灰度化，转化为仅含单通道像素的灰度图像；

2） 按照从左到右、从上到下的顺序依次遍历图像中的所有像素。对于每个像素而言，选取其为中心的3 * 3 邻域；

3） 对于每个邻域，以该邻域中心的像素值作为阈值，其四周的8个像素值与之进行比较，若值大于阈值像素的值，则该位置处被置为1，否则置为0；

4） 经过对比后，在3 * 3邻域内，其四周8个点可产生8位二进制数，将这8位二进制数依次排列组成二进制序列，这个二进制序列的十进制值就是邻域中心的LBP值；

5）对图像内的所有像素遍历后，可得到整幅图像中每个像素经编码后的LBP值，即最终产生的LBP特征。注意，所产生的LBP响应图也为灰度图。

注意！！！
有些论文或者方法中，作者们提取LBP特征时，常从中心像素值右侧中心的点开始排列已经经过比较的值。在Timo Ojala, Matti Pietikainen等人2002年总结的《Multiresolution gray-scale and rotation invariant texture classification with local binary patterns》一文中，我看到圆形LBP是按中心像素值右侧中心的点开始排列的，这种微差别到底有什么区别，待会比较一下看看。

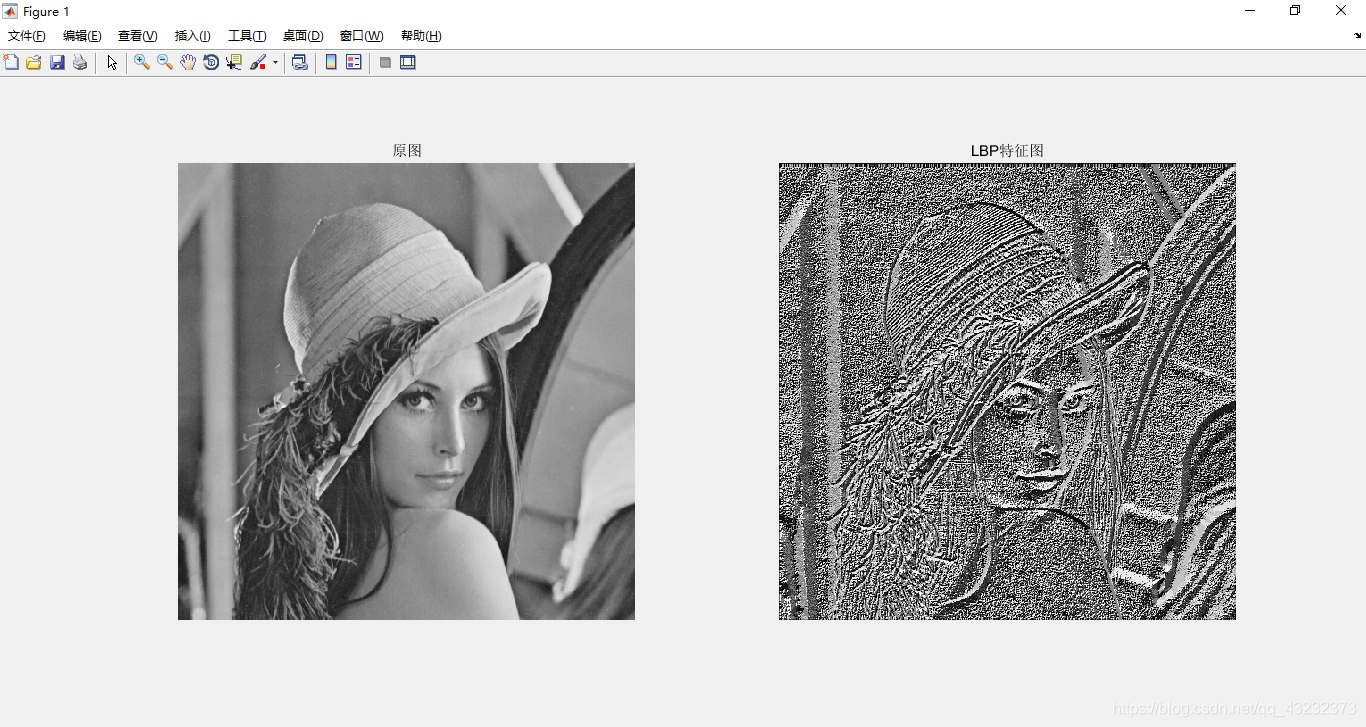
下面是我写的LBP特征的matlab代码，就用它来对比一下两种不同的排列方式提取的LBP特征的对比吧：

close all;I=imread('D:\桌面\Matlab\4.png');
subplot(2,3,1);imshow(I);title('原图');
[m,n]=size(I);     %计算图像大小
%J=rgb2gray(I);
%subplot(2,2,2);imshow(J);title('灰度图');%给图像加一圈边框，以保证3 * 3模板的中心点 可以作用到原图的每一个像素
K=zeros(m+2,n+2); 
for i=1:mfor j=1:nK(i+1,j+1)=I(i,j);end
end
K=uint8(K);
subplot(2,3,2);imshow(K);title('扩充图');Q=zeros(m,n);
for i=2:m+1for j=2:n+1A=zeros(1,8);A(1) = K(i-1,j-1)>K(i,j);A(2) = K(i-1,j)>K(i,j);A(3) = K(i-1,j+1)>K(i,j);A(4) = K(i,j-1)>K(i,j);A(5) = K(i,j+1)>K(i,j);A(6) = K(i+1,j-1)>K(i,j);A(7) = K(i+1,j)>K(i,j);A(8) = K(i+1,j+1)>K(i,j);for u=1:8Q(i-1,j-1) = Q(i-1,j-1)+A(u)*2^(8-u);endend
end
Q=uint8(Q);
subplot(2,3,3);imshow(Q);title('LBP特征图');[a,b]=size(Q);
h=zeros(1,256);
for i=1:mfor j=1:nk=Q(i,j); h(k+1)=h(k+1)+1;end
end
subplot(2,3,4);plot(h);%axis([0,250,0,6000]);
title('LBP特征灰度直方图');
subplot(2,3,5); imhist(Q);title('函数实现');

LBP的整体思想非常简单，计算复杂度很低，反映的特征较好，但是有两个明显问题：

1. 3×3邻域模板过小，无法捕获大尺度纹理结构；

2. 矩形模板是不具有旋转不变性。

因此就有了基于LBP的改进方法。

圆形LBP特征：Circle LBP

这个概念在2002年Ojala等人发表的《Multiresolution gray-scale and rotation invariant texture classification with local binary patterns》进行了详细介绍。
如下图所示，定义中心点为gc，从最右中间点开始计数g0-gP-1共P（P>1）个点，它们等角均匀地分布在半径为R（R>0）的圆周上。以gc为原点（0, 0），圆周上的点gp坐标为(-Rsin(2πp/P), Rcos(2πp/P))，如果点没有落到像素中心，则采用插值的方式进行估计近似，通常来说使用双线性插值。

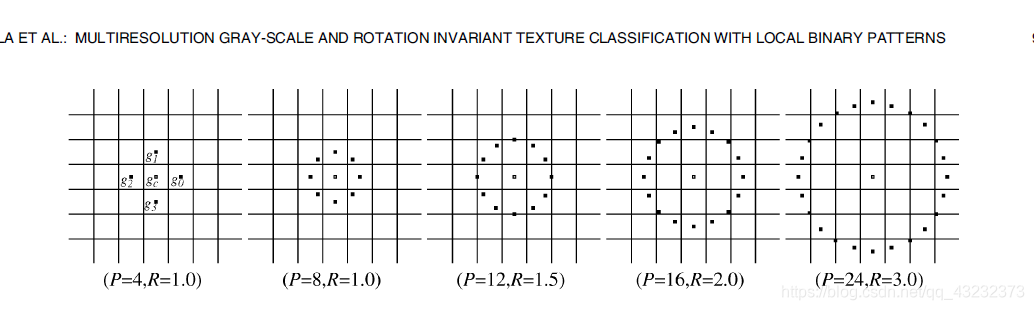
这样就可以通过改变P的值在圆上添加任意多个点，也可以通过改变R的值任意改变模板大小，记这样的LBP算子为：

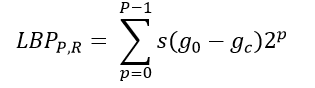
然而圆形LBP依然不具有旋转不变性，且在人脸识别，表情识别方面应用很少，这里我们就不展开详解了。

旋转不变LBP特征：LBPROT

我们总是选择最右中间点作为起始点g0，所以当LBP算子旋转的时候，g0会发生变化，这样即使是同一个模板、同一个位置、同样的P、R，计算得到的LBP特征值都是不同的。为了消除这种旋转差异，重新定义了LBP计算方式：

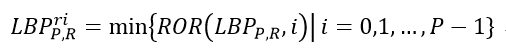
其中ROR(x,i)指的是对p位数字x进行i次循环右移。也就是说，从各个旋转的LBP二进制串中，找到最小的值，作为这个模板的LBP特征。举个例子，假设P=8，R=1（8个点，半径1），那么对于4个连续的1，4个连续的0（00001111）来说，可以旋转的有：

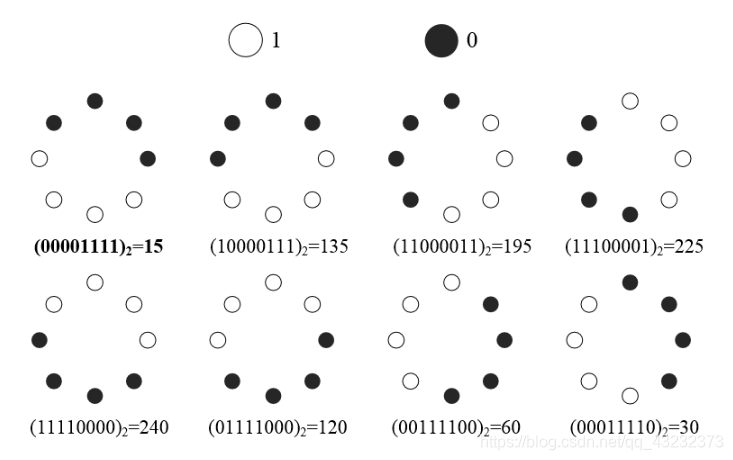
显然最小的是15，所以这个模板的值就是15。

看起来圆形LBP很完美，但实际使用发现LBPROT并不具有很好地辨别力，因为随着采样点数的增加，二进制模式会急剧增多，会使得数据量过大，直方图过于稀疏，不能很好地反映图像特征。

等价LBP特征： ULBP

针对圆形LBP缺点，Ojala进一步提出等价LBP特征，利用等价模式来对LBP模板种类进行降维。我们首先定义“跳变”为二进制串中"01"、"10"这样的变化，定义度量准则（Uniformity measure U(“pattern”)）为二进制串中的跳变次数。Ojala等人发现，图像中大部分包含的都是至多两种跳变，且这些囊括了“亮点”、‘暗点’、‘平坦区域’、‘变化的边缘’等等，基本包含了绝大部分主要信息。

所以，Ojala等人将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类。

通过这样的改进，二进制模式的种类大大减少，而不会丢失任何信息。模式数量由原来的2P种减少为 P ( P-1)+2种，其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说，二进制模式由原始的256种减少为58种，这使得特征向量的维数更少，并且可以减少高频噪声带来的影响。公式如下：

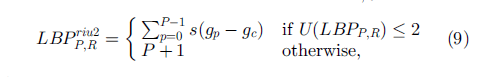
ULBP应用于原始3 * 3模板的话，提取步骤如下：
1） 输入图像若为彩色图像，则将其灰度化，转化为仅含单通道像素的灰度图像；

2） 按照从左到右、从上到下的顺序依次遍历图像中的所有像素。对于每个像素而言，选取其为中心的3 * 3 邻域；

3） 对于每个邻域，以该邻域中心的像素值作为阈值，其四周的8个像素值与之进行比较，若值大于阈值像素的值，则该位置处被置为1，否则置为0；

4） 经过对比后，在3 * 3邻域内，其四周8个点可产生8位二进制数，将这8位二进制数依次排列组成二进制序列，依次计算每个8位二进制数的“01”，“10”跳变次数，若跳变次数小于等于2，则将该二进制序列对应的十进制值就是邻域中心的LBP值；若跳变次数大于2，则直接将邻域中心点的LBP值置为 P+1， 也就是9。

5）对图像内的所有像素遍历后，可得到整幅图像中的LBP值，即最终产生的ULBP特征。
实现代码待续。

旋转不变等价LBP特征： ULBP-ROT

结合旋转不变LBP与 等价LBP的特点，暂时没看明白，等读懂了再分析。