马蹄集matji oj赛（第十二次）

2023-10-13 20:15
文章标签 oj matji 第十二次 马蹄

本文主要是介绍马蹄集matji oj赛（第十二次），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

元素共鸣

欧拉函数

欧拉函数2

小码哥的喜欢数

整数的逆

数的自我

阶乘的质因子

分数个数

质数率

数字游戏

元素共鸣


难度：黄金
0时间限制：1秒
巴占用内存：128M
遥远的大陆上存在着元素共鸣的机制。
建立一个一维坐标系，其中只有素数对应的点的坐标存在着元素力，而相距为飞的两个元素力之
间能形成元素共鸣。现在，需要求出范围内所有能元素共鸣的点对，并将他们以第一个点的坐
标大小为关键字排序后输出（小的在前）。
格式
输入格式：一行两个整数几，k。
输出格式：所有小于等于的素数对。每对素数奴对输出一行，中间用单个空格隔开。
若没有找到任何素数对，输出empty。

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
const int N =1e4+ 7;
bool judge[N];
int prime[N],cnt;
int getPrimes(int n) {for (int i = 2; i <= n; i++) {if (!judge[i])prime[cnt++] = i;for (int j = 0; prime[j] * i <= n; j++) {judge[prime[j] * i] = true;if (i % prime[j] == 0)break;}}return cnt;
}
int main(){int n,k;bool flag = false;cin >>n >>k;getPrimes(n);for (int i=0;i<cnt;i++) {int n1 = prime[i], n2 = n1 + k;if (n2 <= n && !judge[n2]) {cout << n1 << " " << n2 << endl;flag = true;}}if (!flag)cout <<"empty";return 0;}

欧拉函数


难度:黄金时间限制: 1秒四占用内存:128M
给出给定正整数 n，求 f(n)，此处 f(n)定为小于n 的所有与n 素的数的个数
格式
一个整数n。输入格式:
输出格式:输出一行一个整数表示答案
样例1
输入:4
输出:2

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
int n;
int euler_phi(int n){int ans = n;for (int i=2;i*i<=n;i++)if(n%i==0) {ans = ans / i * (i - 1);while (n % i == 0) n /= i;}if (n > 1) ans=ans /n *(n -1);return ans;}int main(){cin >>n;cout <<euler_phi(n);return 0;}

欧拉函数2


难度: 钻石时间限制: 1秒四占用内存: 128M
给出给定正整数 n，求”f()，此处 f(n)定义为小于等于 n 并且与 n 质的数的个数(此处认为 1与1互质)
格式
输入格式:一个正整数n。
输出格式:输出一行一个整数表示答案
样例1
输入:4
输出:6

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 +7;
bool judge [N];
int prime [N],cnt,phi[N],n,sum;
void getPhi(int n){phi[1]=1;for (int i=2;i<=n;i++) {if (!judge[i]) {prime[cnt++] = i;phi[i] = i - 1;}for (int j = 0; prime[j] * i <= n; j++) {judge[prime[j] * i] = true;if (i % prime[j] == 0) {phi[prime[j] * i] = prime[j] * phi[i];break;} elsephi[prime[j] * i]=(prime[j] - 1) * phi[i];}}
}signed main() {cin >> n;getPhi(n);for (int i = 1; i <= n; i++)sum += phi[i];cout << sum << endl;return 0;}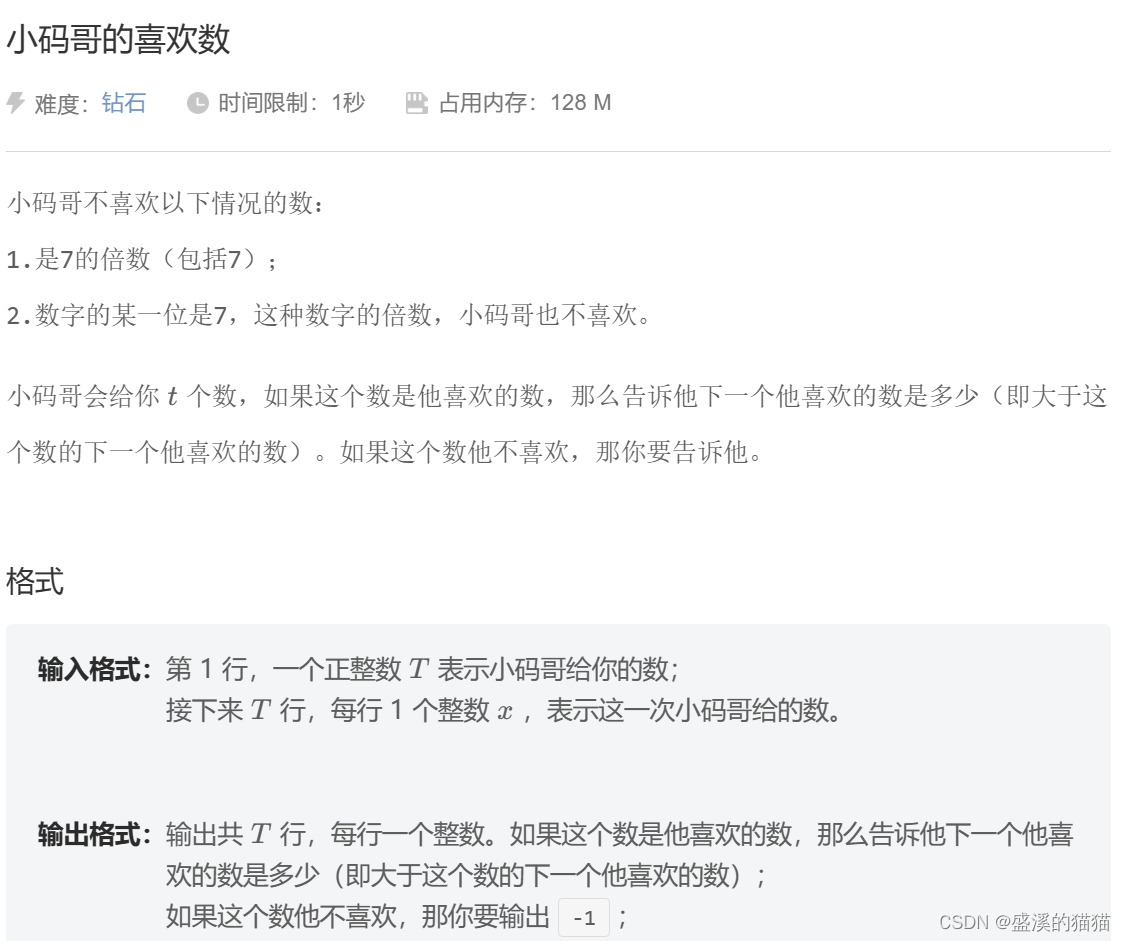

小码哥的喜欢数


难度: 钻石
时间限制: 1秒四占用内存:128M
小码哥不喜欢以下情况的数:
1.是7的倍数(包括7);
2.数字的某一位是7，这种数字的倍数，小码哥也不喜欢。
小码哥会给你 t个数，如果这个数是他喜欢的数，那么告诉他下一个他喜欢的数是多少(即大于这个数的下一个他喜欢的数)。如果这个数他不喜欢，那你要告诉他。
格式
输入格式:第1行，一个正整数T表示小码哥给你的数接下来T行，每行1个整数2，表示这一次小码哥给的数
输出格式:输出共T行，每行一个整数。如果这个数是他喜欢的数，那么告诉他下一个他喜欢的数是多少(即大于这个数的下一个他喜欢的数) ;如果这个数他不喜欢，那你要输出 -1 ;

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
const int N = 1e7 +7;
int T,x,ans [N],nxt [N],cnt;
bool judge[N]={1};
bool check(int x) {while (x) {if (x % 10 == 7)return true;x /= 10;}return false;
}int getNums(int n){int curr = 1;for (int i=2;i<=n;i++){if (!judge[i]) {bool flag = check(i);if (!flag) {ans[cnt++] = i;nxt[curr] = i;curr = i;} else {for (int j = i; j <= n; j += i)judge[j] = true;}}}return cnt;}int main(){getNums(N);cin >>T;while (T--){cin >>x;if (judge[x])cout <<-1 <<endl;else{cout <<nxt[x]<<endl;}
}
return 0;
}

整数的逆


难度:黄金时间限制: 1秒四占用内存:128M
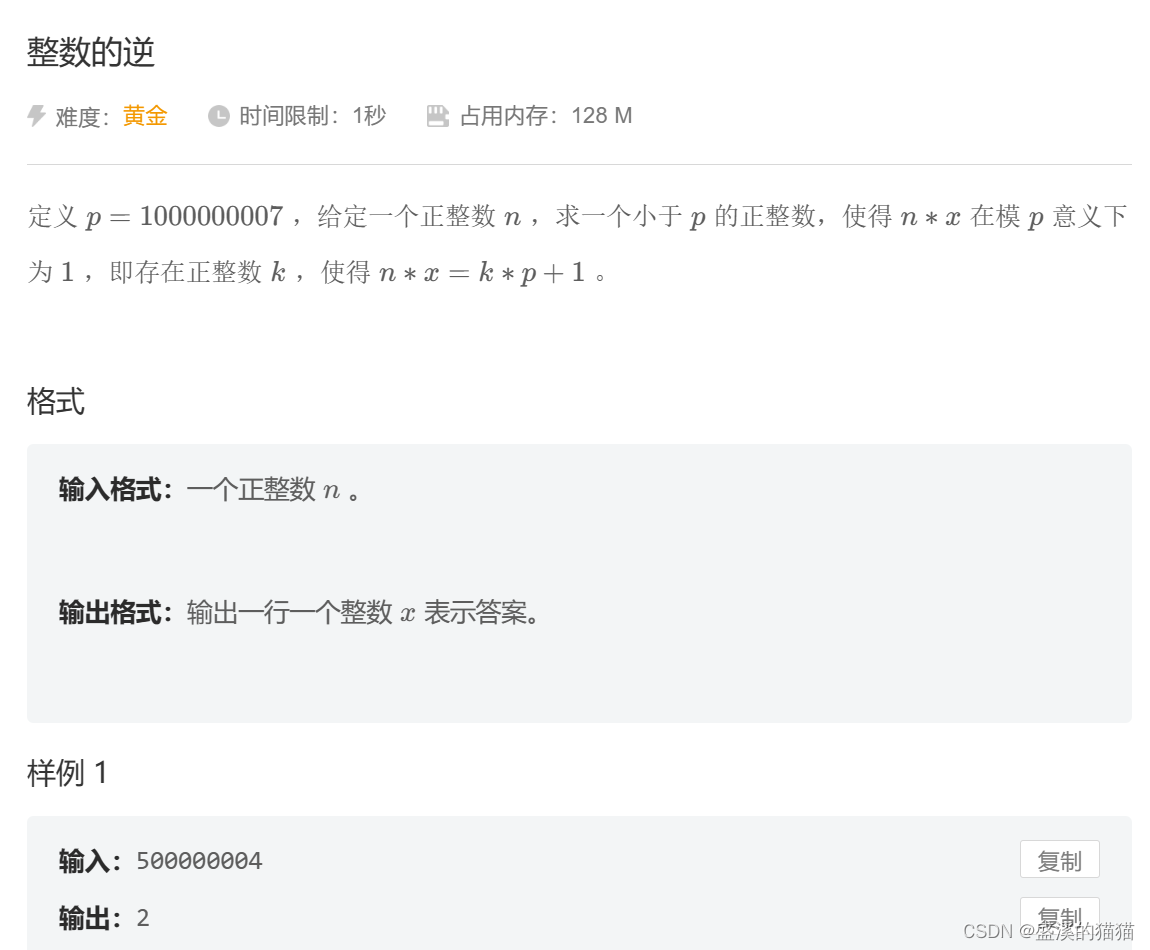
定义p=1000000007，给定一个正整数n，求一个小于p 的正整数，使得 n * 在p 意义下为1，即存在正整数 k，使得n*e=k*p+1。
格式
一个正整数n。输入格式:
输出格式:输出一行一个整数  表示答案
样例1
输入: 500000004
输出:2

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n,mod = 1e9 +7;
long long binpow(long long a,long long b,long long m){a%=m;long long res = 1;while (b > 0){if (b & 1)res = res * a % m;a=a * a % m;b>>=1;
}
return res;
}
signed main(){cin >>n;cout <<binpow(n,mod -2,mod);return 0;
}

数的自我


难度: 钻石时间限制: 0.75秒四占用内存:128M
提瓦特大陆上有一个贫穷的占星术士小码哥，出于占星术的要求，他时常要解决一些困难的数学问题。这天，上天给了他一个启示: 有一类称作 Self - Numbers 的数。对于每一个正整数 n，我们定义 d(n)为n加上它每一位数字的和。例如， d(75)= 75+7+5=87。给定任意正整数 n作为一个起点，都能构造出一个无限递增的序列: n,d(n),d(d(n)),d(d(d(n))),...例如,如果你从33开始，下一个数是33+3+3=39，再下一个为39+3+9=51，再再下一个为51+5+1=57，因此你所产生的序列就像这样:33，39，51，57，69，84，96，111，114，120，123，129,141，... 数字n被称作d(n)的发生器。在上面的这个序列中，33是39的发生器，39是51的发生器51是57的发生器等等。有一些数有超过一个发生器，如101的发生器可以是91和100。一个没有发生器的数被称作 Self- Number 。如前13个 Self -Number 为1，3，5，7，9，20，31,42，53，64，75，86，97。我们将第i个 Self-Number 表示为ai，所以a1=1,a2] = 3,a 3 =5...
现在小码哥需要找到一个1N 的区间内所有的 Self-Number ，请你帮帮他。

//
// Created by abner on 2023/10/11.
//#include <bits/stdc++.h>
using namespace std;
const int N=1e7 +7;
int ans[N],cnt,n,k;
bool judge[N];
int cal(int x) {int ans = x;while (x) {ans += x % 10;x /= 10;}return ans;
}
int getNums(int n) {for (int i = 1, temp; i <= n; i++) {temp = cal(i);if (temp <= n)judge[temp] = true;if (!judge[i])ans[cnt++] = i;}return cnt;
}int main(){cin >>n >>k;cout <<getNums(n)<<endl;int x;while (k--) {cin >> x;cout << ans[x - 1] << " ";}return 0;}

阶乘的质因子


难度:钻石时间限制: 1秒占用内存: 128 M
小码哥有一天想把20!表示出来，但是小码哥意识到这个数字算出来将非常大，于是你给小码哥出主意，用算术基本定理的形式表示，于是这个任务理所应当的被小码哥推给了你，正好你想干点简单的事来换换脑子，就接受了。你要把 N! 按照算术基本定理的形式表示。
基本算数定理:一个数一定可以用一下形式表示:a = p(1]1] * p(2)c2l*..... *p(jl ;
pli 为质数数组， cl 为每一个质数的幂的次数对于不同的 a 来说，有不同的 p 和 c 数组。
格式
输入格式:输入一个整数N
输出格式: N!分解质因数后的结果，共若干行，每行两个数 p,c,表示含有 p项。按照

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 +7;
bool judge [N];
int prime[N],cnt,n;
int getPrimes(int n) {for (int i = 2; i <= n; i++) {if (!judge[i])prime[cnt++] = i;for (int j = 0; prime[j] * i <= n; j++) {judge[prime[j] * i] = true;if (i % prime[j] == 0)break;}}return cnt;
}signed main(){cin >> n;getPrimes(n);for (int i=0;i<cnt;++i){int ans =0,r=prime[i];while (r <= n){ans +=n /r;r *= prime[i];}if (ans)cout <<prime[i] <<" "<<ans <<endl;}return 0;}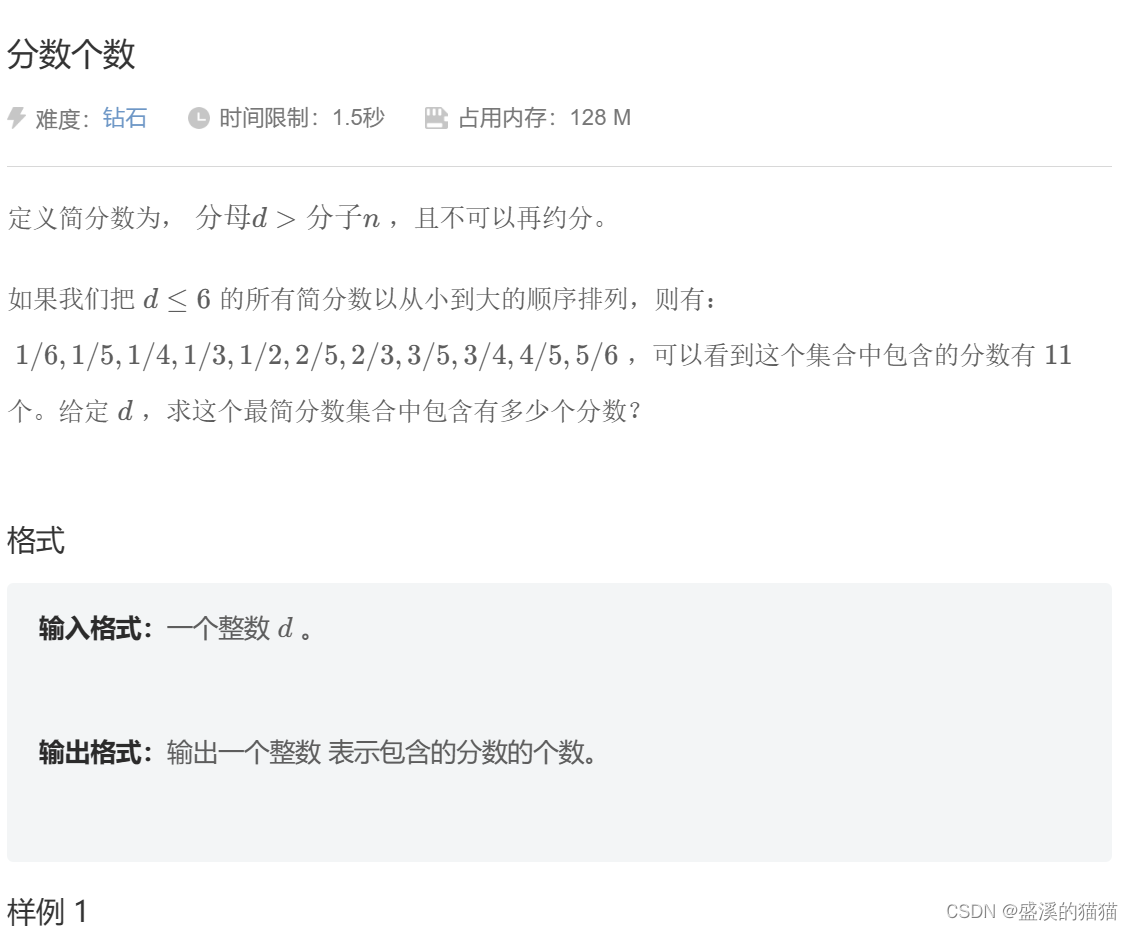

分数个数


难度: 钻石时间限制: 1.5秒四占用内存:128M
定义简分数为，分母d >分子n ，且不可以再约分
如果我们把 d< 6 的所有简分数以从小到大的顺序排列，则有:1/6,1/5,1/4,1/3,1/2,2/5,2/3,3/5,3/4,4/5,5/6 ，可以看到这个集合中包含的分数有11个。给定 d ，求这个最简分数集合中包含有多少个分数?
格式
输入格式:一个整数 d.
输出格式:输出一个整数表示包含的分数的个数

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 7;
bool judge [N];
int prime [N],cnt,phi[N],n,sum;
void getPhi(int n){phi[1]=1;for (int i=2;i<=n;i++){if (!judge[i]){prime[cnt++] = i;phi[i] = i-1;}for (int j=0;prime[j]* i<=n;j++) {judge[prime[j] * i] = true;if (i % prime[j] == 0) {phi[prime[j] * i] = prime[j] * phi[i];break;} elsephi[prime[j] * i] = (prime[j] - 1) * phi[i];}}
}
signed main(){cin >>n;getPhi(n);for (int i = 2;i <= n;i++)sum += phi[i];cout <<sum <<endl;return 0;
}

质数率


难度:黄金时间限制: 1秒四占用内存:256M
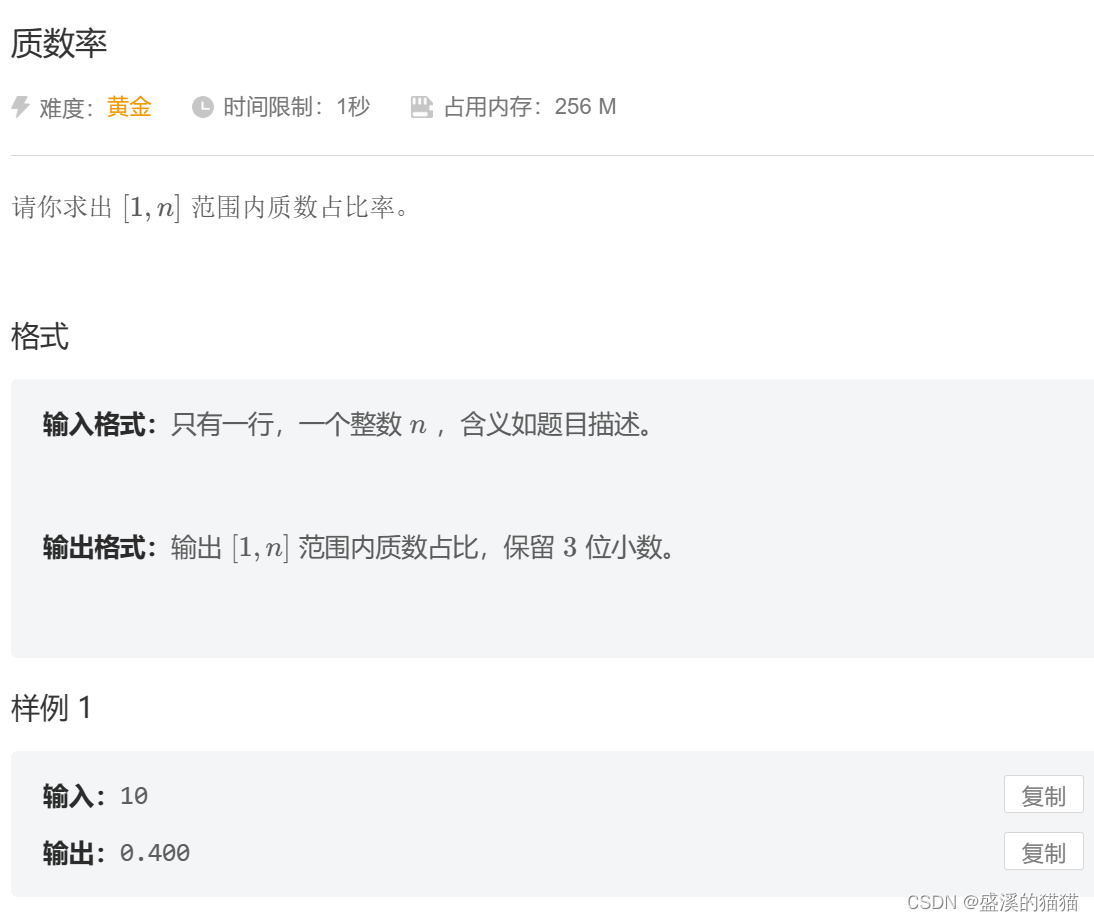
请你求出 1,n 范围内质数占比率
格式
输入格式:只有一行，一个整数 n ，含义如题目描述。
输出格式:输出[1,n 范围内质数占比，保留3 位小数
样例1
输入:10
输出:8.409

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
const int N = 1e8 +7;
bool judge[N];
int prime[N],cnt,n;
int getPrimes(int n) {for (int i = 2; i <= n; i++) {if (!judge[i])prime[cnt++] = i;for (int j = 0; prime[j] * i <= n; j++) {judge[prime[j] * i] = true;if (i % prime[j] == 0)break;}}return cnt;
}
int main(){scanf("%d",&n);getPrimes(n);printf("%.3lf\n",(double)cnt/n);return 0;
}

数字游戏


难度:黄金时间限制: 1秒四占用内存:128 M
小码哥和小码妹正在玩一个小游戏，小码哥先展示一个正整数 n，如果小码妹可以写出 k个正整数21···2k 满足]I-(+ 1)=n，则她可以得到  分。小码妹的数学并不好，所以请你写一个程序帮忙计算她最多可以得到多少分。
格式
输入格式:一行，一个正整数 n e2,1x 108
输出格式:一行，一个正整数
样例1
输入:12

//
// Created by abner on 2023/10/11.
//
#include <bits/stdc++.h>
using namespace std;
int n,ans;
int main(){cin >>n;for (int i = 2;i*i<=n;i++)while(n%i== 0) {ans++;n /= i;}if(n>1)ans++;cout <<ans;return 0;
}

这篇关于马蹄集matji oj赛（第十二次）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/205608。

相关文章

哈理工OJ 2179(深搜)

哈理工OJ 2179(深搜)

组合 Time Limit: 1000 MSMemory Limit: 32768 K Total Submit: 7(5 users)Total Accepted: 6(5 users)Rating: Special Judge: No Description 给出一个正整数N，从集合{1,2,3..N} 中找出所有大小为k的子集, 并按照字典序从小到大输出。 Input 第一行是一个整
阅读更多...
每日OJ_牛客_求和（递归深搜）

每日OJ_牛客_求和（递归深搜）

目录 牛客_求和（递归深搜） 解析代码 牛客_求和（递归深搜） 求和_好未来笔试题_牛客网 解析代码         递归中每次累加一个新的数，如果累加和大于等于目标，结束递归。此时如果累加和正好等于目标，则打印组合。向上回退搜索其它组合。此题本身就是一个搜索的过程，找到所有的组合。 #include <iostream>#include <cmath>#in
阅读更多...
OJ-0905

OJ-0905

题目 示例1： 输入：10 10 56 34 99 1 87 8 99 3 255 6 99 5 255 4 99 7 255 2 99 9 255 213 4输出：99 示例2： 输入：10 10 255 34 0 1 255 8 0 3 255 6 0 5 255 4 0 7 255 2 0 9 255 213 5输出：255 import java.util.
阅读更多...
每日OJ_牛客_Emacs计算器（逆波兰表达式）

每日OJ_牛客_Emacs计算器（逆波兰表达式）

目录 牛客_Emacs计算器（逆波兰表达式） 解析代码 牛客_Emacs计算器（逆波兰表达式） Emacs计算器__牛客网 解析代码 逆波兰表达式(后缀表达式)求值，需要借助栈，思路： 循环输入，获取逆波兰表达式，然后进行以下补助，直到测试完所有的测试用例： 遇到数字字符串，将该数字字符串转化为数字然后入栈。遇到操作符时，从栈顶取两个数字，然后进行该运算符所对应运算
阅读更多...
西北工业大学oj题-兔子生崽

西北工业大学oj题-兔子生崽

题目描述： 兔子生崽问题。假设一对小兔的成熟期是一个月，即一个月可长成成兔，每对成兔每个月可以生一对小兔，一对新生的小兔从第二个月起就开始生兔子，试问从一对兔子开始繁殖，一年以后可有多少对兔子？ 这道题目一眼看过去就是典型的递归问题，代码如下 public class RabbitReproduction {public static void main(String[] args) {in
阅读更多...
★ 算法OJ题 ★ 力扣209 - 长度最小的子数组

★ 算法OJ题 ★ 力扣209 - 长度最小的子数组

Ciallo～(∠・ω< )⌒☆ ~ 今天，简将和大家一起做一道滑动窗口算法题--长度最小的子数组~ 目录 一  题目 二  算法解析 解法⼀：暴力求解 解法二：滑动窗口 三  编写算法 一  题目 209. 长度最小的子数组 - 力扣（LeetCode） 二  算法解析 解法⼀：暴力求解 算法思路： 从前往后枚举数组中的任意⼀个元素，把它当成起始位置
阅读更多...
OJ-0903

OJ-0903

题目 示例1 输入：30 12 25 8 19输出：15 示例2 输入：10 12 25 8 19 8 6 4 17 19 20 30输出：-1 题解 import java.util.ArrayList;import java.util.List;import java.util.Scanner;public class Main {public static
阅读更多...
【负载均衡式在线OJ】Compile_server 模块

【负载均衡式在线OJ】Compile_server 模块

文章目录 程序源码compile_server整体思路编译(compile.hpp)运行模块编译运行模块编译运行服务 程序源码 https://gitee.com/not-a-stupid-child/online-judge compile_server 整体思路 这个服务要对oj_server 发送过来的代码进行编译和运行，最后把结果返回给oj_server。 所以我
阅读更多...
★ 算法OJ题 ★ 力扣18 - 四数之和

★ 算法OJ题 ★ 力扣18 - 四数之和

Ciallo～(∠・ω< )⌒☆ ~ 今天，爱丽速子将和大家一起做一道双指针算法题--四数之和~ 目录 一  题目 二  算法解析 三  编写算法  做此题前最好先看一下前两篇博客~： ★ 算法OJ题 ★ 力扣 LCR179 - 和为 s 的两个数字-CSDN博客 ★ 算法OJ题 ★ 力扣15 - 三数之和-CSDN博客 一  题目 18. 四数之和 - 力扣（Lee
阅读更多...
oj生成数据

oj生成数据

首先先写一个生成test.in的代码，利用随机数生成测试数据。 按照格式生成测试数就行   转载：https://blog.csdn.net/qq_29980371/article/details/72825443 #include <bits/stdc++.h>using namespace std;int main(){freopen("test.in","w",stdout);
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2