【题解】P3469 [POI2008]BLO-Blockade
图论割点好题!
题目链接
P3469 [POI2008]BLO-Blockade - 洛谷
题意概述
给定一张无向图,求每个点被封锁之后有多少个有序点对 \((x,y)(x \ne y,1 \le x,y \le n)\) 满足 \(x\) 无法到达 \(y\)。
思路分析
首先需要说明一个易错点,即有序点对,即 \((x,y)\) 和 \((y,x)\) 算作不同的点对,也就是计数的时候要算两遍。
显然答案的数量与当前节点是否为割点有关。
那么我们分类讨论,设原图共有 \(n\) 个节点,对于当前节点 \(i\):
-
若节点 \(i\) 不是割点,则把节点 \(i\) 关联的所有边删掉后,只有节点 \(i\) 与其它 \(n-1\) 个节点不连通,其它 \(n-1\) 个节点间还是互相连通的。
所以答案是 \(2(n-1)\)。
-
若节点 \(i\) 是割点,则把节点 \(i\) 关联的所有边删掉后,图会分裂为多个连通块。
显然任意两个连通块的节点间都不能互相到达。
根据乘法原理和加法原理,设有 \(k\) 个连通块,且第 \(i\) 个连通块的大小是 \(siz_i\),则每一个连通块对答案的贡献就是
\[ans_i=\sum \limits_{j=1}^k(j \ne i)siz_i \times siz_j。 \]那么总的答案就是
\[\sum \limits_{i=1}^k ans_i=\sum \limits_{i=1}^k \sum \limits_{j=1}^k (j\ne i)siz_i \times siz_j \]现在问题就转化为要求删掉节点 \(i\) 关联的所有边后,原图分裂为多少个连通块,以及每个连通块的大小是多少。
一个小 trick 就是,在图论的连通性问题上,我们经常从 dfs 树的角度来分析。
假设在 dfs 树上,有 \(t\) 个点 \(s_1,s_2,s_3,\cdots,s_t\) 满足 \(low_{s_k} \ge dfn_i\),那么在删掉节点 \(i\) 相连的所有边后,无向图至多分成 \(t+2\) 个连通块:
-
节点 \(i\) 单独构成一个连通块;
-
有 \(t\) 个连通块,分别由 dfs 树上以 \(s_k(1\le k \le t)\) 为根的子树中的节点构成;
-
还可能有一个连通块由除上述之外的其它所有节点构成。
这块可能相对抽象,画个图来理解一下:

如图,dfs 树上 3,5 这两个节点的 \(low\) 值 \(\ge dfn_i\)。
删掉 \(i\) 相连的所有边后:
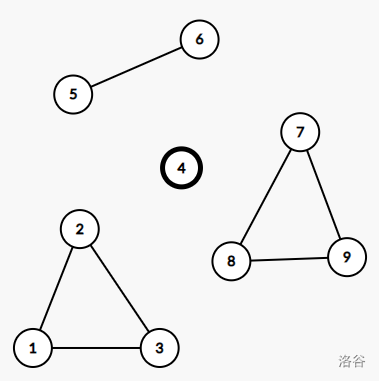
无向图分裂为四个连通块,分别是:节点 4 本身,以 3 为根的节点所在连通块,以 4 为根的节点所在连通块,剩下的 7,8,9 构成的连通块。
我们可以在 Tarjan 求割点时,顺便记录 dfs 树上每个节点的子树大小,设 \(sz_x\) 表示以 \(x\) 为根的子树大小。
则每个 \(s_i\) 对答案的贡献为:\(sz_{s_i} \times(n-sz_{s_i})\)。(子树内所有点与子树外任意一点都不联通)
所以 \(t\) 个以 \(s_i(1\le i\le t)\) 为根的子树总共对答案的贡献为:
\[\sum \limits_{i=1}^t sz_{s_i} \times (n-sz_{s_i}) \]节点 \(i\) 对答案的贡献为:\(n-1\)。(\(i\) 与其它 \(n-1\) 个节点均不连通)
剩下的其它点对答案的贡献为:
\[(1+\sum \limits_{i=1}^t sz_{s_i})\times (n-1-\sum \limits_{i=1}^t sz_{s_i}) \]所以总的答案就是:
\[\sum \limits_{i=1}^t sz_{s_i} \times (n-sz_{s_i})+(n-1)+(1+\sum \limits_{i=1}^t sz_{s_i})\times (n-1-\sum \limits_{i=1}^t sz_{s_i}) \] -
易错点
有序点对意味着 \((x,y)\) 和 \((y,x)\) 是不同的点对,要计数两次。
代码实现
//luoguP3469
#include<iostream>
#include<cstdio>
#include<cstring>
#define int long long
#define mk make_pair
using namespace std;
const int maxn=1e5+10;
const int maxm=5e5+10;
int tot;
int n,m;
int dfn[maxn],low[maxn],vis[maxn],siz[maxn],ans[maxn]; basic_string<pair<int,int> >edge[maxn];inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}void dfs(int x,int pre)
{dfn[x]=low[x]=++tot;siz[x]=1;int ret=0,sum=0;for(auto nxt:edge[x]){int y=nxt.first,id=nxt.second;if(!dfn[y]){dfs(y,x);siz[x]+=siz[y];low[x]=min(low[x],low[y]);if(low[y]>=dfn[x]){ans[x]+=siz[y]*(n-siz[y]);//对于每一个满足条件的点累加其贡献。ret++;sum+=siz[y];//sum 是剩下的点的个数。} }else if(id!=pre)low[x]=min(low[x],dfn[y]);}if(ret>=2||(ret==1&&pre)){vis[x]++;//将 x 标记为割点。ans[x]+=(n-1)+(n-sum-1)*(sum+1);//加上 x 本身和剩下的点的贡献。}return ;
}signed main()
{n=read();m=read();for(int i=1;i<=m;i++){int u,v;u=read();v=read();edge[u]+=mk(v,i);edge[v]+=mk(u,i);//无向图 }for(int i=1;i<=n;i++){if(!dfn[i])dfs(i,0);}for(int i=1;i<=n;i++){if(!vis[i])cout<<2*(n-1)<<'\n';//不是割点。else cout<<ans[i]<<'\n';//是割点。}return 0;
}
/*思路
首先分类讨论。
当 i 不为割点时,显然除 i 之外的其它点均联通,
只有 i 与剩下的 n-1 个节点之间不连通。即答案为 2*(n-1)
当 i 为割点时,显然当 i 删掉后,将其分成几个连通块。
那么答案就是联通块大小相乘再相加的结果(乘法加法原理)
*/





