本文主要是介绍代码随想录算法训练营第二十天丨 二叉树part07,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
530.二叉搜索树的最小绝对差
思路
题目中要求在二叉搜索树上任意两节点的差的绝对值的最小值。
注意是二叉搜索树,二叉搜索树是有序的。
遇到在二叉搜索树上求什么最值啊,差值之类的,就把它想成在一个有序数组上求最值,求差值,这样就简单多了。
递归
那么二叉搜索树采用中序遍历,其实就是一个有序数组。
在一个有序数组上求两个数最小差值,【遍历顺序:左中右】
最直观的想法,就是把二叉搜索树转换成有序数组,然后遍历一遍数组,就统计出来最小差值了。
但是,可以更简单,像上述说的解题方法还需要额外去申请该数组的空间,并且代码也比较繁琐。
这里其实可以用 pre 结点记录 cur 结点的前一个结点。
图:
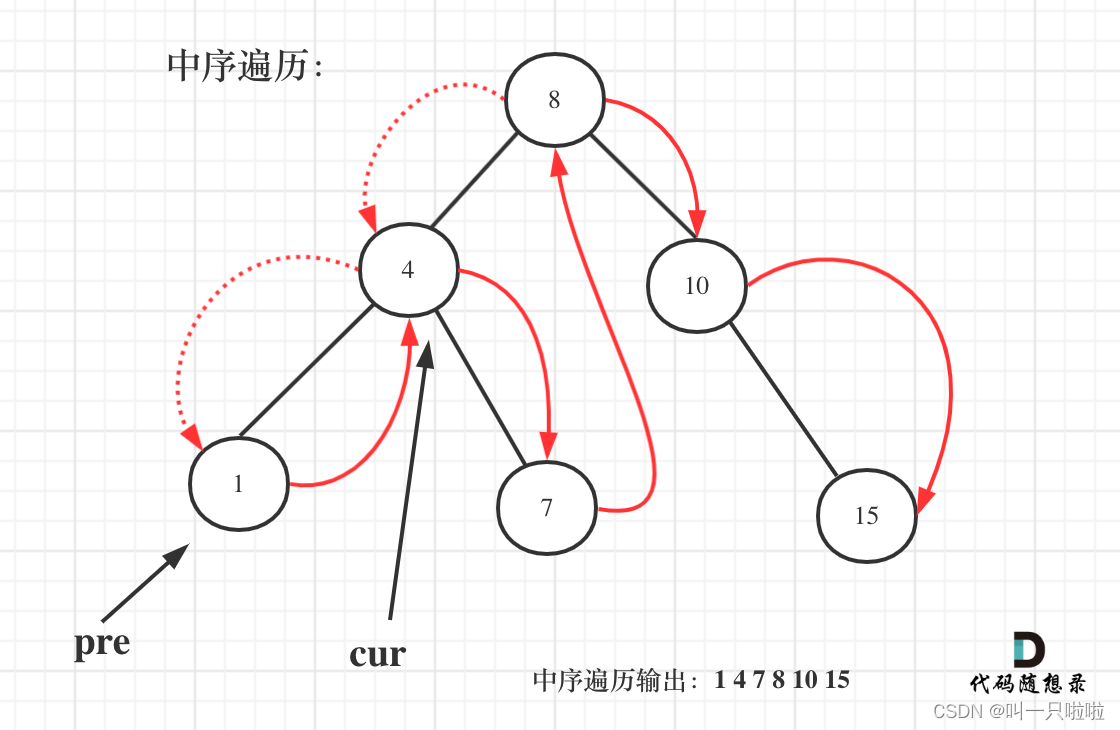
代码:
class Solution {public int getMinimumDifference(TreeNode root) {getMin(root);return min;}// 记录上一个遍历的结点TreeNode pre = null;int min = Integer.MAX_VALUE;void getMin(TreeNode cur){//终止条件if (cur == null){return;}//左getMin(cur.left);//中if (pre != null){min = Math.min(min, cur.val - pre.val);}pre = cur;//右getMin(cur.right);}
}总结
遇到在二叉搜索树上求什么最值,求差值之类的,都要思考一下二叉搜索树可是有序的,要利用好这一特点。
501.二叉搜索树中的众数
思路
递归法
#如果不是二叉搜索树
如果不是二叉搜索树,最直观的方法一定是把这个树都遍历了,用map统计频率 ,把频率排个序,最后取前面高频的元素的集合。
是二叉搜索树
既然是搜索树,它中序遍历就是有序的。
如图:
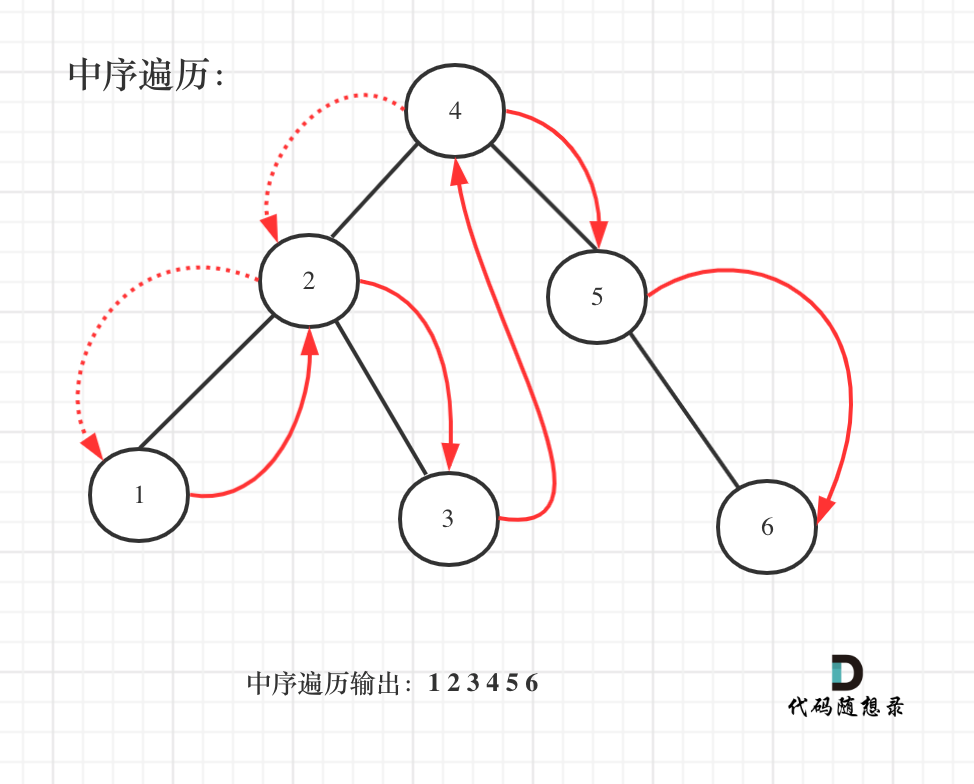
遍历有序数组的元素出现频率,从头遍历,那么一定是相邻两个元素作比较,然后就把出现频率最高的元素输出就可以了。
关键是在有序数组上的话,在树上怎么搞呢?
在二叉树:搜索树的最小绝对差 (opens new window)中我们就使用了pre指针和cur指针的技巧,这次又用上了。
弄一个指针指向前一个节点,这样每次cur(当前节点)才能和pre(前一个节点)作比较。
而且初始化的时候pre = NULL,这样当 pre为NULL 时候,我们就知道这是比较的第一个元素。
代码如下:
if (pre == null){count = 1;}//碰到中序遍历的第一个节点时
else if (pre.val == cur.val){count++;}// 与前一个节点数值相同
else {// 与前一个节点数值不同count = 1;
}
pre = cur;//更新上一结点此时又有问题了,因为要求最大频率的元素集合(注意是集合,不是一个元素,可以有多个众数)
应该是先遍历一遍数组,找出最大频率(maxCount),然后再重新遍历一遍数组把出现频率为maxCount的元素放进集合。(因为众数有多个)
这种方式遍历了两遍数组。
那么我们遍历两遍二叉搜索树,把众数集合算出来也是可以的。
但这里其实只需要遍历一次就可以找到所有的众数。
那么如何只遍历一遍呢?
如果 频率count 等于 maxCount(最大频率),当然要把这个元素加入到结果集中(以下代码为result数组),代码如下:
if (maxCount == count){//当该值出现的次数为最大出现频率时,添加到数组中res.add(cur.val);
}
是不是感觉这里有问题,result怎么能轻易就把元素放进去了呢,万一,这个maxCount此时还不是真正最大频率呢。
所以下面要做如下操作:
频率 count 大于 maxCount 的时候,不仅要更新maxCount,而且要清空结果集(以下代码为result数组),因为结果集之前的元素都失效了。
else if (count > maxCount) {// 如果计数大于最大值res.clear();// 很关键的一步,不要忘记清空result,之前result里的元素都失效了maxCount = count;// 更新最大频率res.add(cur.val);
}//当该值出现的次数小于最大出现频率时,不做任何改变完整代码如下:
class Solution {//存放结果集ArrayList<Integer> res = new ArrayList<>();//用于记录单个元素出现的次数int count = 0;//用于记录树中出现频率最高的次数int maxCount = 0;//指针,用于比较当前结点和当前结点的前一结点TreeNode pre = null;public int[] findMode(TreeNode root) {findTree(root);int[] result = new int[res.size()];for (int i = 0; i < res.size(); i++) {result[i] = res.get(i);}return result;}void findTree(TreeNode cur){//终止条件if (cur == null){return;}//左findTree(cur.left);//中if (pre == null){count = 1;}//碰到中序遍历的第一个节点时else if (pre.val == cur.val){count++;}// 与前一个节点数值相同else {// 与前一个节点数值不同count = 1;}pre = cur;//更新上一结点if (maxCount == count){//当该值出现的次数为最大出现频率时,添加到数组中res.add(cur.val);} else if (count > maxCount) {// 如果计数大于最大值res.clear();// 很关键的一步,不要忘记清空result,之前result里的元素都失效了maxCount = count;// 更新最大频率res.add(cur.val);}//当该值出现的次数小于最大出现频率时,不做任何改变//右findTree(cur.right);}
}236. 二叉树的最近公共祖先
思路
遇到这个题目首先想的是要是能自底向上查找就好了,这样就可以找到公共祖先了。
这样就要用到 回溯 了,二叉树回溯的过程就是从低到上。
后序遍历(左右中)就是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。
首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。 即情况一:
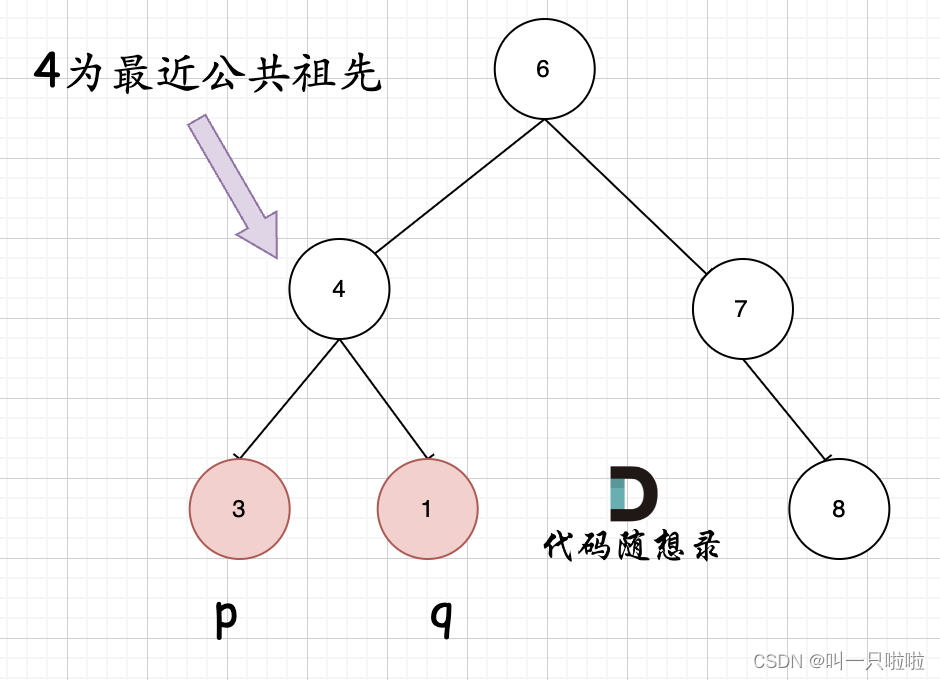
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
但是很多人容易忽略一个情况,就是节点本身p(q),它拥有一个子孙节点q(p)。 情况二:
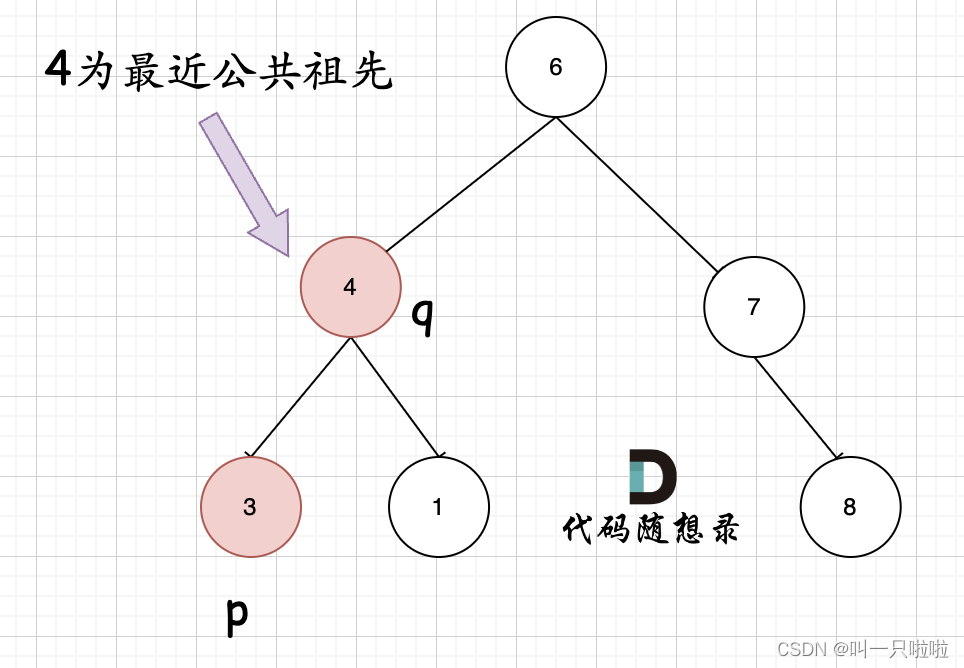
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
因为遇到 q 或者 p 就返回,这样也包含了 q 或者 p 本身就是 公共祖先的情况。
具体代码如下:【详细讲解 : 代码随想录】
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {return findAncestor(root,p,q);}TreeNode findAncestor(TreeNode node, TreeNode p, TreeNode q){//递归终止条件if (node == null){return node;}if (node == p || node == q){return node;}//单层递归逻辑//左TreeNode left = findAncestor(node.left, p, q);// 右TreeNode right = findAncestor(node.right, p, q);// 中if (left != null && right != null){//如果当前结点找到了 p 和 q,直接返回当前结点return node;} else if (left != null && right == null){//如果只找到了其中一个 或者 p 是 p 和 q的最近公共祖先return left;} else if (left == null && right != null) {return right;}else {//都没找到直接返回return null;}}
}以上为我做题时候的相关思路,自己的语言组织能力较弱,很多都是直接抄卡哥的,有错误望指正。
这篇关于代码随想录算法训练营第二十天丨 二叉树part07的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






