本文主要是介绍KPCA降维的matlab代码,贡献率,累积贡献率,可设置降维数目,可设置核函数,可设置核参数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
不用担心代码质量问题,直接复制吧,家人们!
先上简单易懂的主函数
clear
close all
clc
load data.mat
X1=data; %data是一个N*M的矩阵,N是样本个数,M是维度!不要整乱了哦!
[X1,~]=mapminmax(X1'); %做个归一化处理,归一化处理的时候要对数据转置的哦
choice = 1; % 1代表高斯核,2代表多项式核,3代表线性核,4代表指数核,5代表拉普拉斯核
sigma = 8; % 核参数
target_dimension = 15 ; % KPCA降维后保留的维度
[X1_KPCA,contrb] = myKPCA(X1, sigma, choice, target_dimension);
data是一个N*M的矩阵,N是样本个数,M是维度!不要整乱了哦!
运行完之后,X1_KPCA就是你想要的降维后的序列,而contrb就是你想要的贡献率咯!
一共两个子函数,首先把这个函数“啪叽”粘贴到你的马特兰博。
function [X_KPCA,contrb] = myKPCA(X, sigma, choice, target_dimension, varargin)
%MYPCM - The Kernel Principal Component Analysis(KPCA) function.
% To calculate the result after KPCA, one kind of
% dimension-reduction technical of characteristics.
% Here are some useful reference material:
% https://www.jianshu.com/p/708ca9fa3023
% https://blog.csdn.net/qq_38517310/article/details/79387476
%
% [eigenvalue, X_KPCA] = myKPCA(x, sigma, cls, target_dim)
%
% Input -
% X: a N*M matrix containing M datas with N dimensions;
% sigma: a parameter of kernel function;
% choice: what kind of kernel to be chosen;
% target_dimension: number of dimensions to be reduced to, normally, target_dimension<N;
% DIM: specifies a dimension DIM to arrange X.
% DIM = 1: X(N*M)
% DIM = 2: X(M*N)
% DIM = otherwisw: error
% Output -
% X_KPCA: a target_dimension*M matrix containing M datas with target_dimension dimensions, result of KPCA of data X;
%
% Copyright (c) 2018 CHEN Tianyang
% more info contact: tychen@whu.edu.cn%%
% parameter number check
narginchk(4,5);
narg = numel(varargin);
DIM = [];
switch nargcase 0case 1DIM = varargin{:};otherwiseerror('Error! Input parameter error.');
end
if isempty(DIM)DIM = 1;
end
if DIM == 2X = X';
elseif DIM~=1 && DIM~=2error('Error! Parameter DIM should be either 1 or 2.');
end
% parameter correction test
if ~ismatrix(X)error('Error! Input parameter "X" should be a matrix');
end
[N,M] = size(X); % N*M = 样本维数*样本数,即每一列代表一个数据/样本
if target_dimension > Nwarning('warning! Parameter "target_dim" is not recommended to be larger than parameter "N".');
elseif target_dimension == Nwarning('Warning! There is no dimension-reduction effect.');
end%% core algorithm
% 计算核矩阵 K (实对称矩阵) 【核矩阵 K 的size等于样本数目】
K = zeros(M,M);
for i=1:Mfor j=1:MK(i,j)=mykernel(X(:,i),X(:,j),choice,sigma); % 落实到计算是任意2个【样本】的点积end
end% 计算中心化后的核矩阵KI((实对称矩阵))
% 中心化:使得矩阵【各行各列】的均值为0(本身为实对称矩阵)
% I*k/M: 矩阵 K 的各列均值延拓 M 行, 即矩阵 I*k/M 每行相同;
% k*I/M: 矩阵 K 的各行均值延拓 M 列, 即矩阵 k*I/M 每列相同;
% I*k*I/(M*M): 矩阵 K 所有数据均值构成的一个M*M矩阵;
I = ones(M,M);
kI = K-I*K/M-K*I/M+I*K*I/(M*M);% 计算特征值与特征向量
[V,D] = eig(kI);
D = diag(D);% 按序由大到小排列,其中v整列参与排序
[proper_value_sort, index] = sort(D, 'descend');
V = V(:, index);% 取 KI 最大的 target_dim 个特征值及其对应的特征向量 【!!!特征向量按行排列!!!】
% 注意这里的 特征值 和 特征向量 都是 KI 或 K 的, 不是高维空间中的特征向量
X_KPCA = (V(:, 1:target_dimension))'; % X_KPCA 本身就是原数据 X 经过 KPCA 之后得到的 contrb = zeros(N,2);
contrb(:,1) = proper_value_sort(1:N)/sum(proper_value_sort); % 计算贡献率
for i=1:Ncontrb(i,2) = sum(contrb(1:i,1)); %贡献率之和
endend下面上核函数。这就是计算和矩阵时候用到的核函数 ,也是很多博主为了盈利故意不给大家展示的核函数。在这里我“啪叽”就复制上去啦,然后你啪叽 “不用点赞” 就可以粘贴走了!
function k = mykernel(x,y,choice,var)%
% k = mykernel(x,y,choice,var)
% Input -
% x: input vector;
% y: input vector;
% choice: what kind of kernel to be chosen;
% var: kernel's parameter.
% Output -
% x: result of a kerner function with 2 input vectors.%%
% cls: choose kernel function
if ~isvector(x)||~isvector(y)error('Input error 1.');
end
if length(x)~=length(y)error('Input error 2.');
end
x = x(:);
y = y(:);
if choice == 1k = exp( - norm(x-y)^2/(2*var^2) ); % 高斯核
elseif choice == 2k = (x'*y+1)^var; % 多项式核
elseif choice == 3 k = x'*y; % 线形核
elseif choice == 4k = exp( - norm(x-y)/(2*var^2) ); % 指数核
elseif choice == 5k = exp( - norm(x-y)/var ); % 拉普拉斯核
elseerror('Error! Parameter "choice" should be interger from 1 to 5.');
end最后我“啪叽”把贡献率的庐山真面目给大家粘贴一下啦
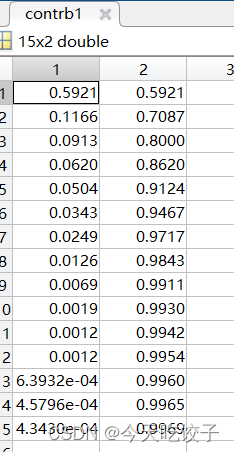
我这里是一个15维度的数据,第一列是每个特征维度的贡献率,第二列是累积贡献率。
这篇关于KPCA降维的matlab代码,贡献率,累积贡献率,可设置降维数目,可设置核函数,可设置核参数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






