自动驾驶 8-2: 平方误差准则和最小二乘法 (下) Squared Error Criterion and the Method of Least Squares (Part 2)

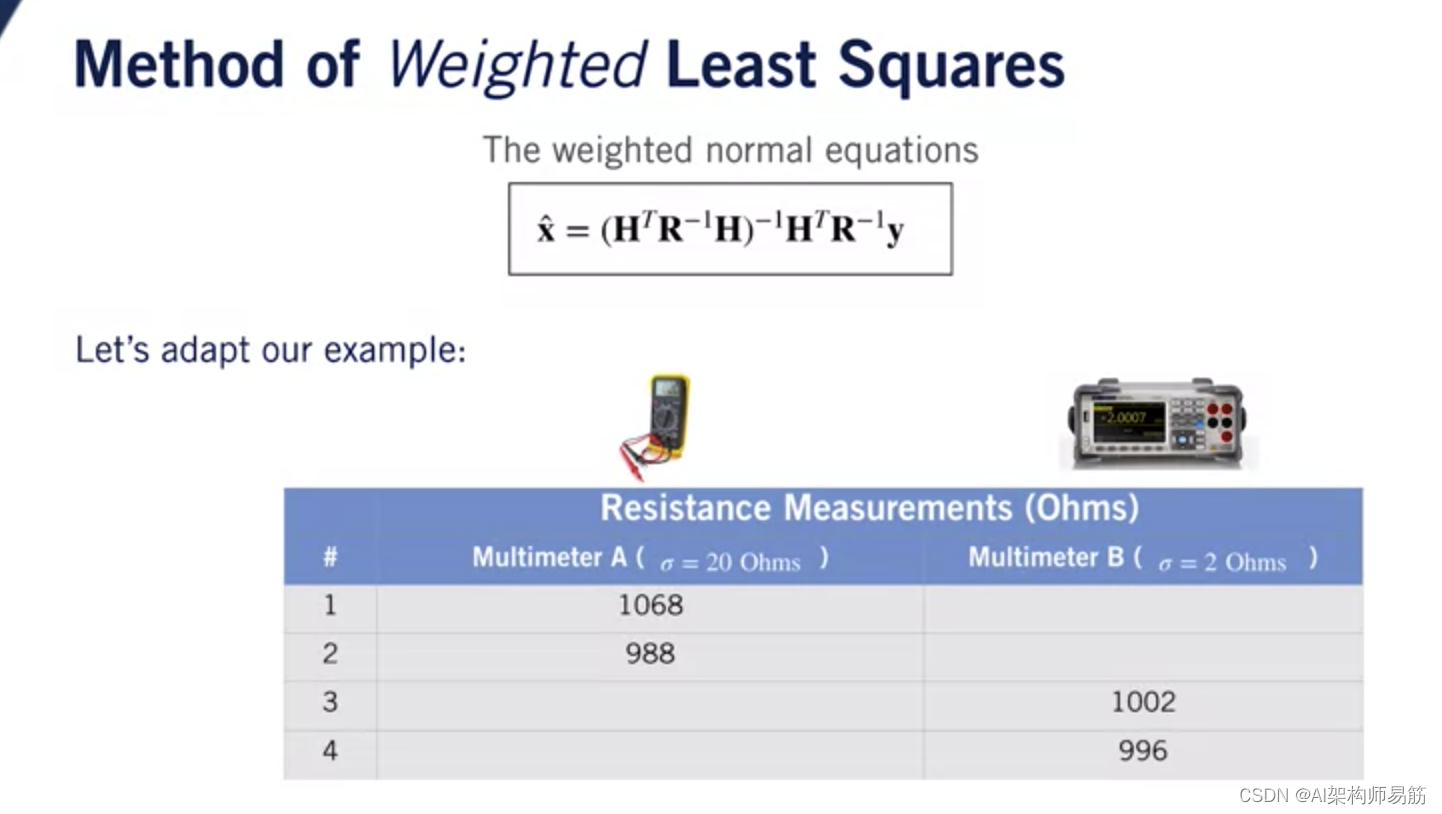
在上一个视频中， 我们看到了如何使用最小二乘法来求解 给出一组噪声测量值的更正确的电阻值。 在这个视频中，我们会问这个问题， 如果我们怀疑某些 我们的测量质量比其他人更好？ 到本视频结束时， 你将能够推导出和最小化 加权最小二乘准则 这将让我们处理测量 不同的质量并将这种新方法与 正则或普通最小二乘法 我们在上一个视频中讨论过。 让我们开始。

我们可能想要信任的原因之一某些测量比其他测量更多 是它们可能来自更好的传感器。

例如，我们的一些电阻测量 可能来自比其他万用表贵得多的万用表。 此外，从现在开始， 我们也将放弃我们只是估计的假设 一个参数并推导出更一般的正规方程。 这将使我们能够制定一种方法 一次估计多个参数。

例如，如果我们想一次估计多个电​​阻值。 让我们从使用以下通用符号开始。

我们将有一组与一组相关的 m 个测量值 n 个未知参数的线性模型。

回想一下 H 是 rj cobian 矩阵 其形式和条目将取决于手头的特定问题。 一种解释普通方法的方法 最小二乘法是说我们隐含地假设 每个噪声项 v_i 是一个独立的随机变量 跨测量并具有 如果您愿意，可以使用相等的方差或标准差， 正如我们在上一个视频中提到的 IID。 如果我们假设每个噪声项都有不同的方差， 我们可以如下定义我们的噪声协方差。

有了这个定义，我们就可以定义一个加权最小二乘准则。 通过扩展这个表达式， 我们可以明白为什么我们称之为加权最小二乘法。 每个平方误差项现在加权 与相应测量相关的方差的倒数。

换句话说，噪声的方差越低， 越强烈 相关的误差项将在损失函数中加权。

我们更关心来自低噪声测量的误差 因为那些应该告诉我们很多关于 我们未知参数的真实值。

在我们看到如何最小化这个新的加权标准之前， 让我们看看如果我们设置所有的会发生什么 噪声标准偏差到相同的值 sigma。

在这种情况下，我们可以分解出分母的方差。 由于 sigma 平方项是 常数它不会影响最小化。

这意味着在方差相等的情况下， 使我们的加权最小二乘准则最小化的相同参数 还将最小化我们的普通最小二乘法 我们应该期望的标准。

回到我们的加权最小二乘标准， 我们像以前一样处理它的最小化， 我们取一个导数。

在一般情况下，我们有 粗体向量 x 中的 n 个未知参数， 这个导数实际上是一个梯度。

设置零向量的梯度， 然后我们求解我们最好的或最优的参数向量 x hat。

这导致另一组正规方程 这一次称为加权正规方程。

让我们看一个例子 这种加权最小二乘法是如何工作的。 我们将采用之前收集的相同数据， 但现在假设最后两次测量实际上是用 噪声方差小得多的万用表。 这里要小心，我们列出的数字是 标准偏差，这就是为什么它们的单位是欧姆。

为了在我们的配方中使用它们， 我们需要对它们进行平方以获得方差。 定义我们的变量，然后 评估我们的加权最小二乘解， 我们可以看到我们得到的最终电阻值是多少 更接近于更准确的万用表按预期测量的结果。

这是方法的快速总结 最小二乘法和加权最小二乘法。

通过使用加权最小二乘法， 我们可以改变每次测量对最终估计的重要性。

与他人一起工作很舒服很重要 不同的测量方差和 也有有时相关的测量。

自动驾驶汽车将有许多不同且复杂的传感器 板，我们需要确保我们正确地建模了我们的错误源。

所以，你有它，加权最小二乘法。

在本视频中，我们讨论了如何 某些测量值可能来自传感器 更好的噪声特性，因此应该 在我们的最小二乘标准中权重更大。

使用这种直觉，我们推导出加权最小二乘准则和 相关的加权正规方程可以求解为 产生一组常数参数的加权最小二乘估计。

在接下来的视频中， 我们将研究修改最小二乘法以递归工作， 即基于流来计算最优估计 测量而无需事先获取整个集合。 当我们查看状态估计时，这将非常重要， 或者估计随时间不断变化的数量的问题。

第 1 课补充阅读：平方误差准则和最小二乘法

补充阅读：平方误差准则和最小二乘法
要了解有关平方误差标准和最小二乘法的更多信息，请查看以下一些资源：

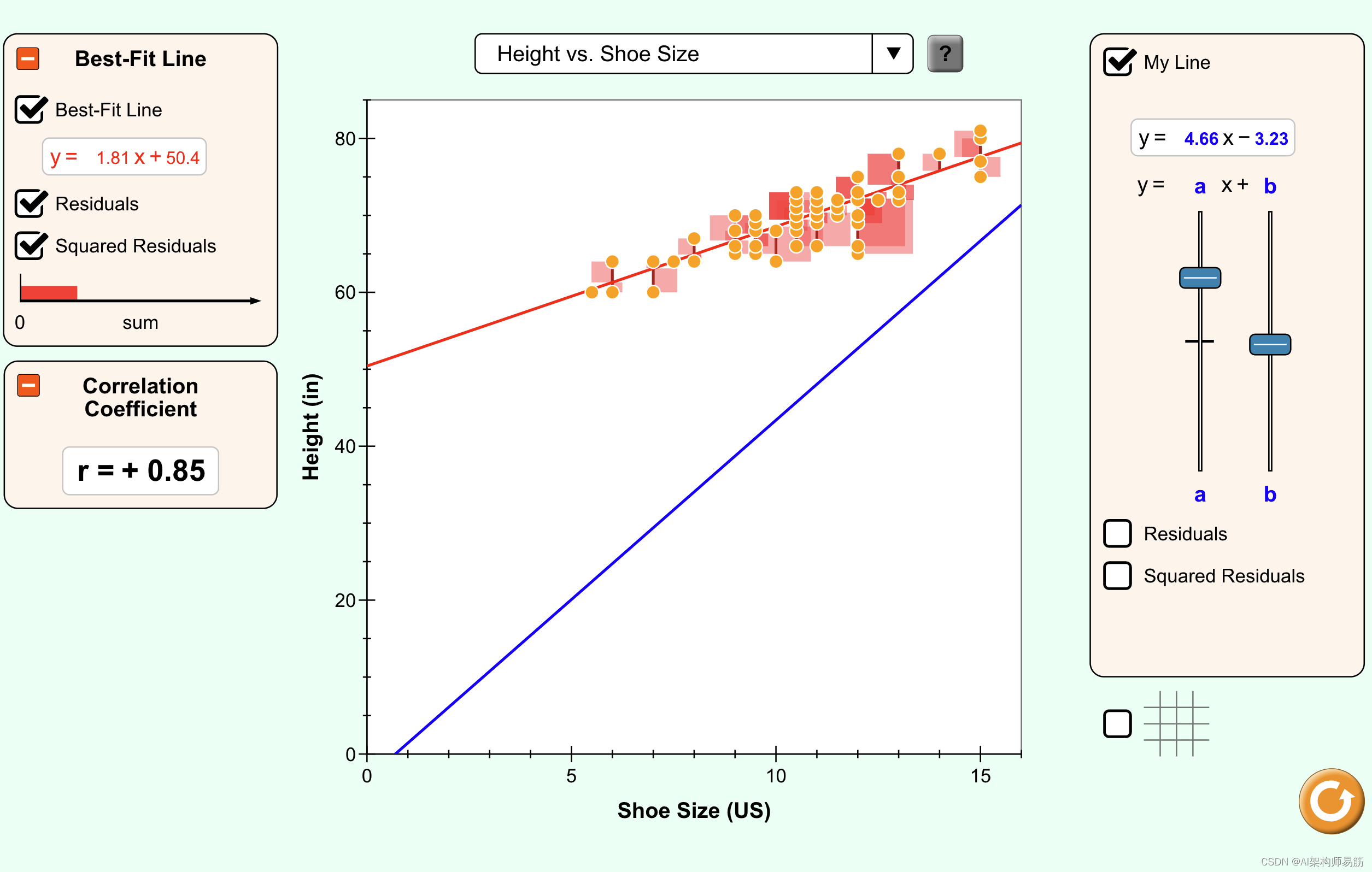
• 这是科罗拉多大学 PhET 交互式模拟项目提供的交互式最小二乘拟合模拟器：https://phet.colorado.edu/sims/html/least-squares-regression/latest/least-squares-regression_en.html
  

• 您可以在佐治亚理工学院的在线教科书中找到关于最小二乘法的概述：Dan Margalit 和 Joseph Rabinoff，交互式线性代数。

• 在Wikipedia上阅读有关最小二乘法的更多信息。

• 阅读Dan Simon, Optimal State Estimation (2006) 的第 3 章第 1 节和第 2 节。

参考

https://www.coursera.org/learn/state-estimation-localization-self-driving-cars/lecture/Ewy9K/lesson-1-part-2-squared-error-criterion-and-the-method-of-least-squares