本文主要是介绍浅尝贝锐蒲公英X1,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
@[(文章目录)贝锐蒲公英X1
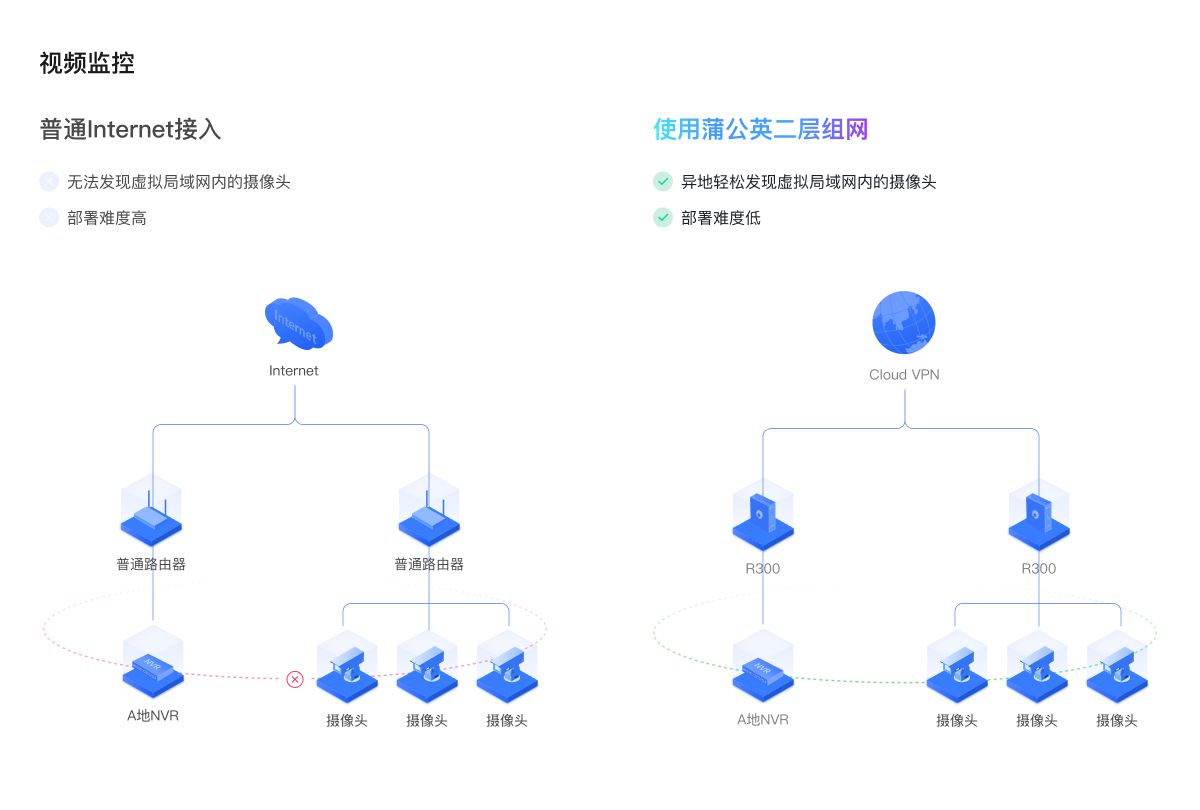
—最近收到一款百元不到就可以实现智能组网、搭建简易私有云、远程访问NAS、云打印等等实用功能,它就是贝锐蒲公英X1;话不多说,开箱验证;
装箱清单:蒲公英X1一台,数据线一条,说明书一本、供电设备直接使用手机充电头,市面上手机充电都支持,Type-C接口完美支持;上图
盒子外观包装
盒内清单
蒲公英X1的顶部是Logo设计,同时也是指示灯,可以根据灯光颜色判定系统当前的状态。侧面接口包括一个百兆网口,一个Type-C电源接口,一个RESET重置孔,以及一个USB接口,能外接移动硬盘或者U盘。

安装方便,插上电源适配器与网线(忽略线乱);
功能界面验证:
输入SN直接绑定设备,So-easy…
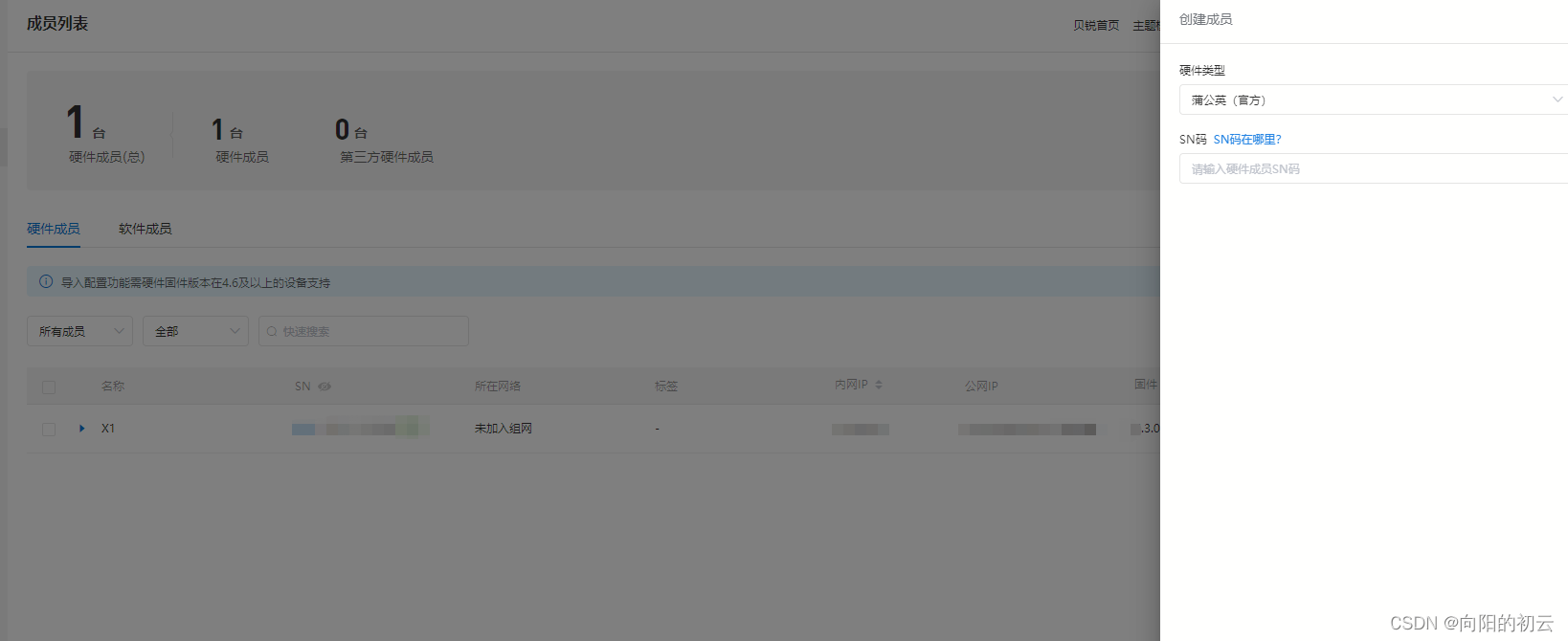
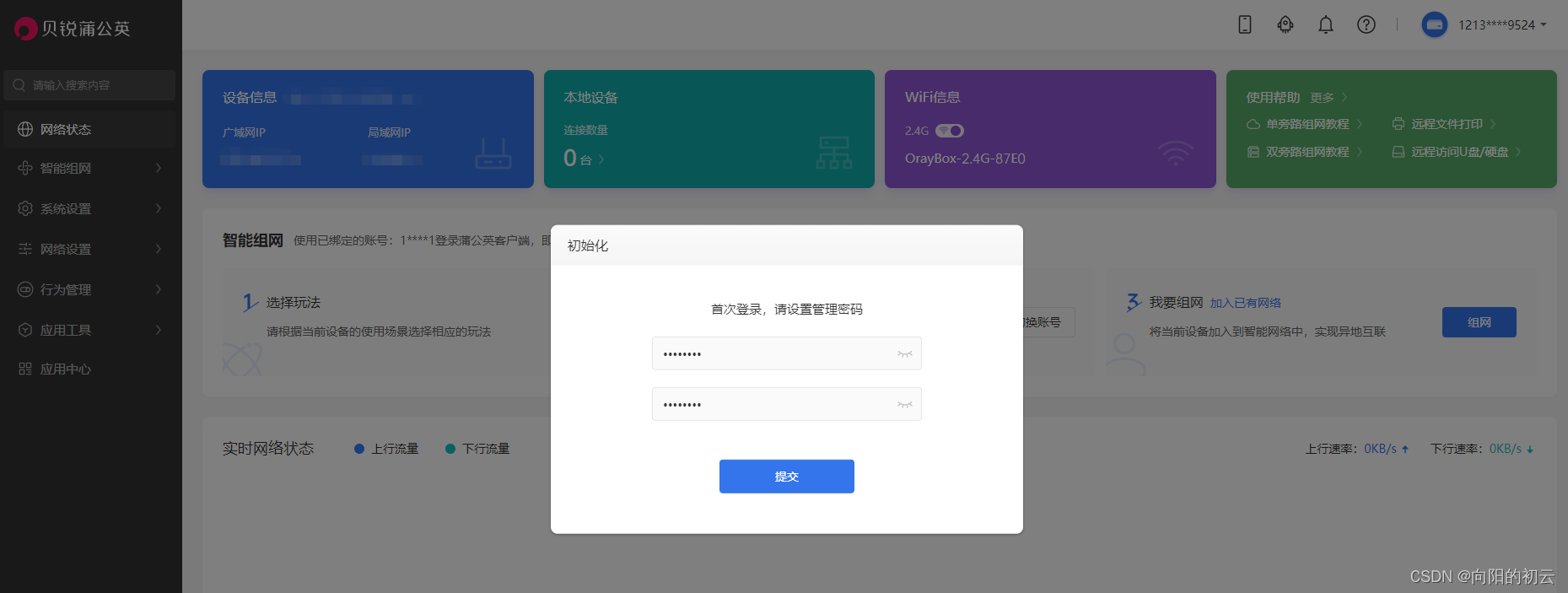
点击管理硬件,进入设备配置参数,也可以选择直接配置参数;
多种玩法随意切换;
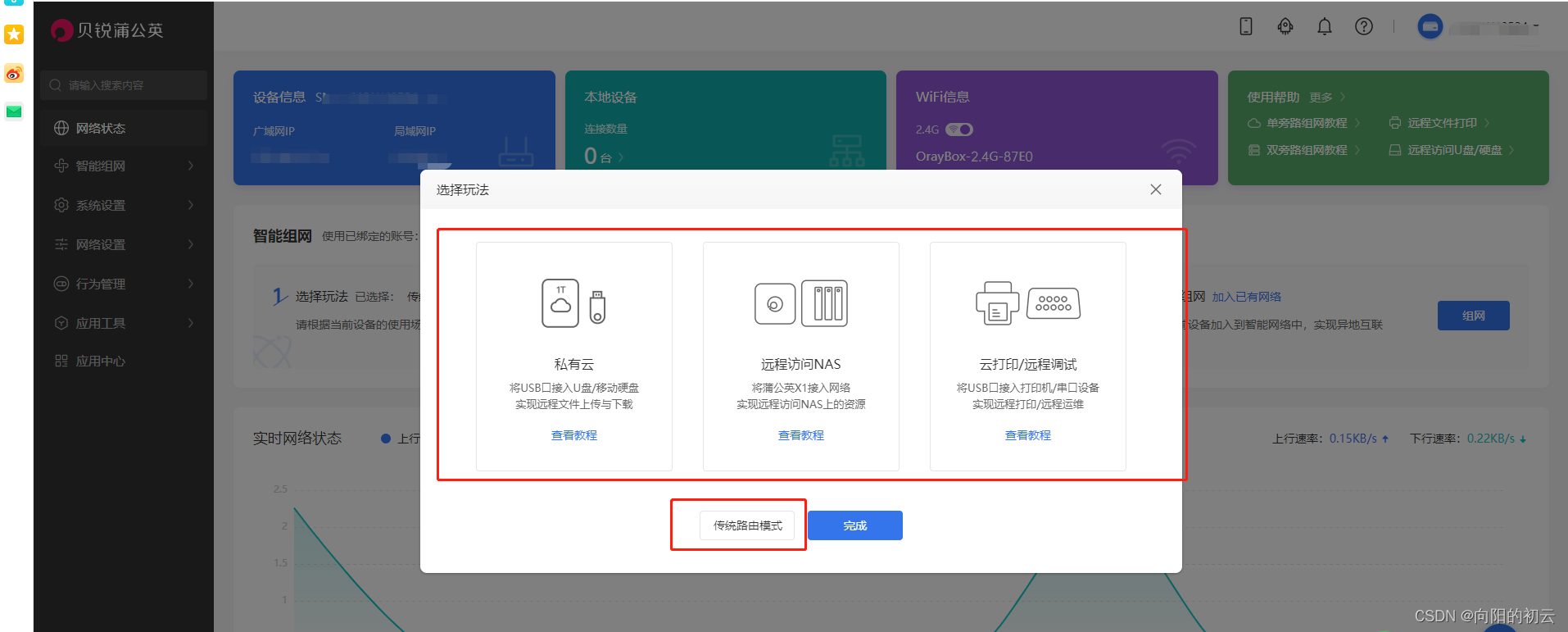
我这里选择私有云组网,接着点击应用中心,选择文件共享。确保已经有U盘或者硬盘接入蒲公英X1。我接入的是1TB的移动硬盘,可以看到移动硬盘已经显现出来了。接下来我们就可以访问U盘里的数据了;(安全起见,建议开启用户与密码访问)
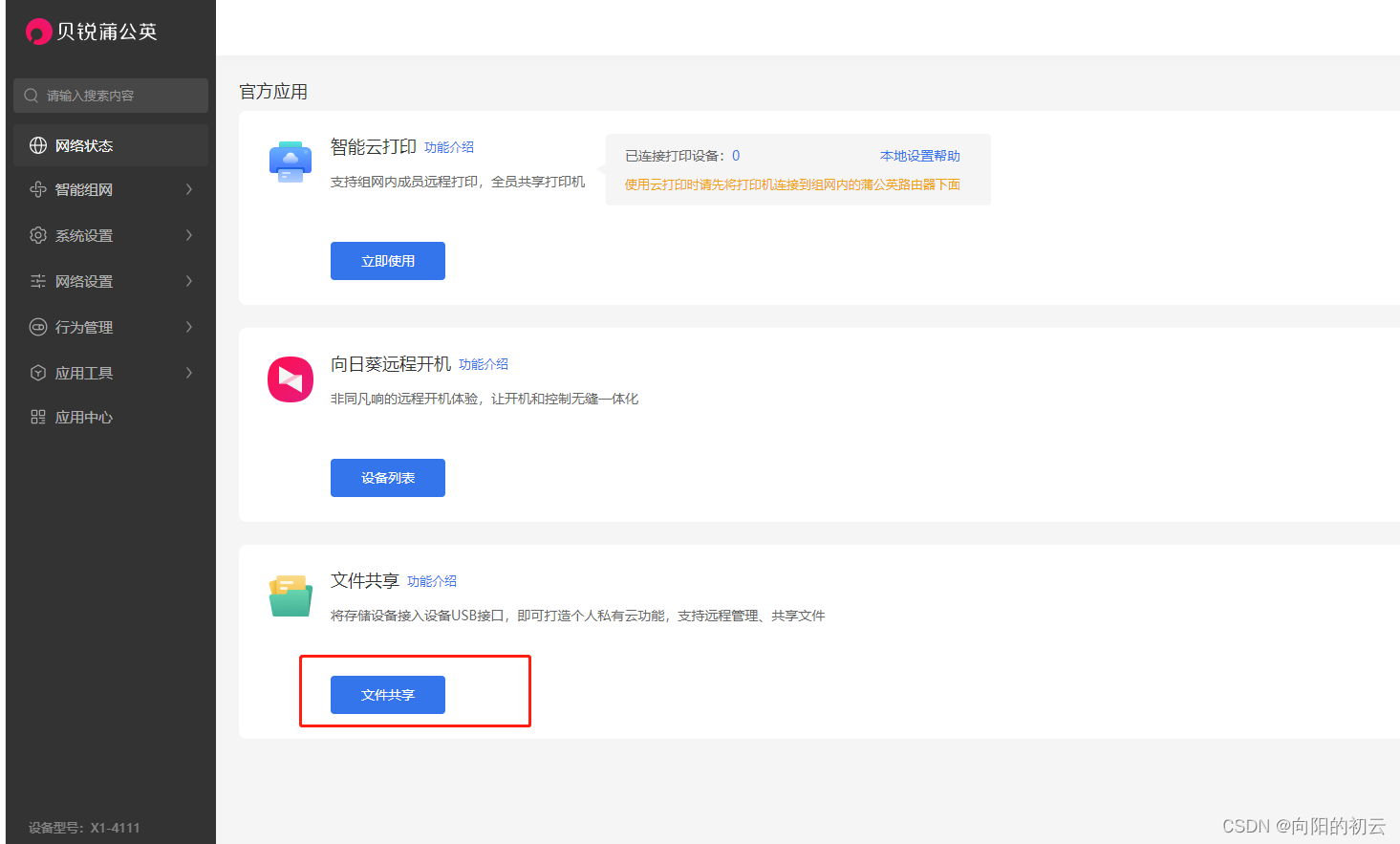
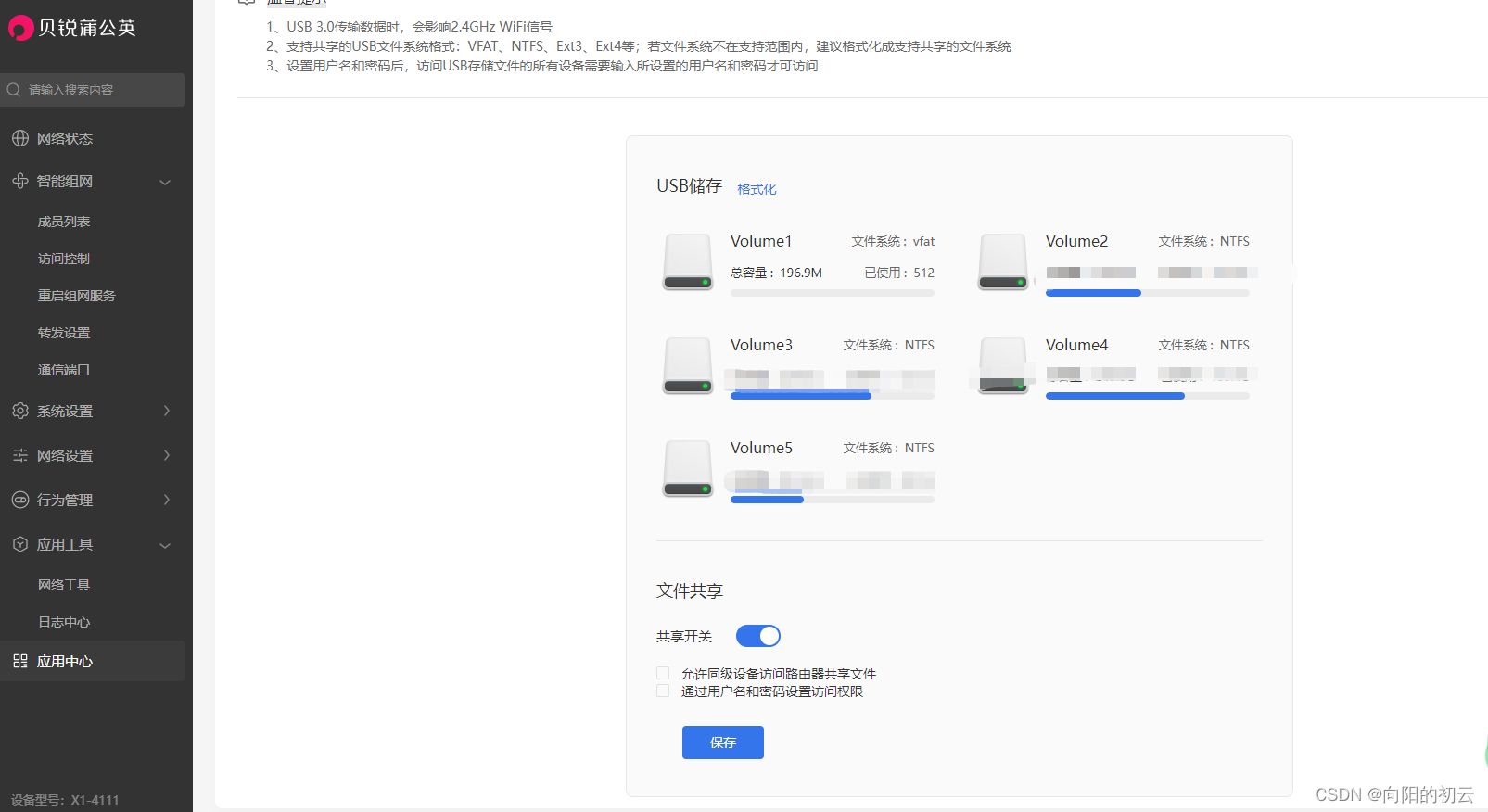
注意事项:需要将设备添加至你需要组网的网络;

在电脑端按下“WIN+R”组合键,在输入框中输入IP地址。就可以访问移动硬盘内部的资料;上传下载的速率取决于你网络带宽质量;
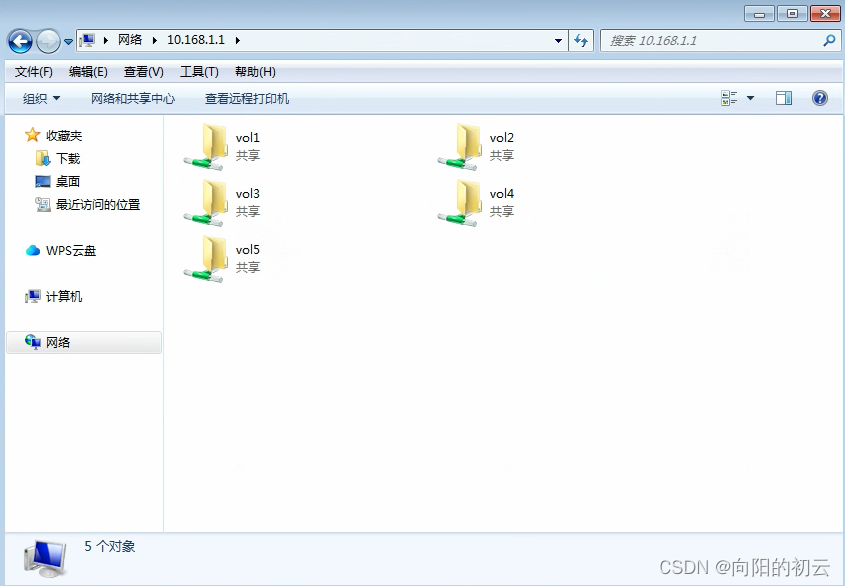
小结一下:
X1盒子组网非常方便,只需要简单几步比设备便可,菜鸟都可以轻松搞定;不仅可以实现异地组网私有云,而且也可以当WIFI上网;但是如果X1设备支持双模就更加完美;
`
这篇关于浅尝贝锐蒲公英X1的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!