本文主要是介绍圖像處理算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
http://blog.csdn.net/shen_wei/article/details/5432566
1)將256*256分辨率的圖像變為128*128分辨率可以將源圖像劃分成2*2的子圖像塊,然後將2*2的
子圖像塊的所有像素顏色均按照F(i,j)的顏色值進行設定,達到降低分辨率的目的。
如:
F(i,j) F(i,j+1) F(i,j) F(i,j)
F(i+1,j) F(i+1,j+1) 變成 F(i,j) F(i,j)
(同理,256*256分辨率的圖像變成64*64分辨率,只需要劃分成4*4即可,以此類推。)
2) R單色, G單色,B單色化圖像,只需要將圖像的每一個像素中的相應的R, G, B值取出,然後利用類似
(R,R,R),(G,G,G),(B,B,B)的像素重新繪制即可。
3) 彩色圖像的RGB和亮度Y,色差I,信號值Q的關系
| Y | |0.31 0.59 0.11 | | R |
| I | = |0.60 -0.28 -0.32 | * | G |
|Q | |0.21 -0.52 -0.31 | | B |
即 Y = 0.31R + 0.59G+0.11B
I = 0.60R - 0.28G - 0.32B
Q = 0.21R - 0.52B - 0.31B
4) 彩色圖像的逆反處理: 將對應的(R, G, B)像素替換成(255 - R, 255 - G, 255 - B)
彩色圖像的平滑處理: 將一個圖片每一個像素的顏色由其相鄰的n*n個像素的平均值來替代。例如,將一個3*3的點陣,設帶平滑的像素為f(i, j),平滑後為g(i, j),那麼
f(i-1,j-1) f(i-1,j) f(i-1,j+1)
f(i,j-1) f(i,j) f(i,j+1)
f(i+1,j-1) f(i+1,j) f(i+1,j+1)
g(i,j)=( f(i-1,j-1) + f(i-1,j) + f(i-1,j+1) + f(i,j-1) + f(i,j) + f(i,j+1) + f(i+1,j-1) + f(i+1,j) + f(i+1,j+1) ) / 9
這裡要注意的是對於邊緣的像素的情況,防止越界。
彩色圖像的霓虹處理: 同樣以上面的3*3的點陣為例,目標像素g(i,j)應當以f(i,j)與f(i,j+1),f(i,j)與f(i+1,j)的梯度作為R,G,B分量,我們不妨設f(i,j)的RGB分量為(r1, g1, b1), f(i,j+1)為(r2, g2, b2), f(i+1,j)為(r3, g3, b3), g(i, j)為(r, g, b),那麼結果應該為
r = 2 * sqrt( (r1 - r2)^2 + (r1 - r3)^2 )
g = 2 * sqrt( (g1 - g2)^2 + (g1 - g3)^2 )
b = 2 * sqrt( (b1 - b2)^2 + (b1 - b3)^2 )
彩色圖像的銳化處理: 設f(i,j)像素為(r1, g1, b1) , f(i-1,j-1)像素為(r2,g2,b2), g(i,j)像素為(r,g,b),則
r = r1 + 0.25 * |r1 - r2|
g = g1 + 0.25 * |g1 - g2|
b = b1 + 0.25 * |b1 - b2|
彩色圖像的浮雕處理: g(i, j) = f(i, j) - f(i - 1, j) + 常數 , 這裡的常數通常選作128
彩色圖像的鑲嵌處理: 與彩色圖像的平滑處理類似,但是不同的地方在於3*3的目標像素點都取作g(i,j),而不是另外的再去取所在矩陣像素的平均值。
彩色圖像的灰度處理: r = r1 / 64 * 64 g = g1 / 64 * 64 b = b1 / 64 * 64 注意這裡的除法是程序設計當中的整數除法。
5) 圖象的幾何變換:平移,縮放,旋轉等均於解析幾何當中的保持一致。
6) 圖象的濾波處理
● 卷積濾波 原理是 y(n1, n2)=ΣΣx(m1,m2)h(n1-m1,n2-m2) (兩個求和符號的范圍分別是 m1:0~N m2:0~N)
其中x(m1,m2)為輸入圖像信號,h(n1-m1,n2-m2)為濾波系統對單位采樣序列δ(n1,n2)的響應。
⊙低通濾波一般而言,圖像中的噪聲頻譜位於空間頻率較高的區域,空間域低通濾波用於平滑噪聲。常用低通濾波的
h(n1, n2) 的3*3陣列如下:
1/9 1/9 1/9
h(n1, n2) = 1/9 1/9 1/9
1/9 1/9 1/9
1/10 1/10 1/10
h(n1, n2) = 1/10 2/10 1/10
1/10 1/10 1/10
1/16 1/8 1/16
h(n1, n2) = 1/8 1/4 1/8
1/16 1/8 1/16
采用5*5陣列低通濾波h(n1,n2)如下:
1/35 1/35 1/35 1/35 1/35
1/35 2/35 2/35 2/35 1/35
h(n1, n2) = 1/35 2/35 3/35 2/35 1/35
1/35 2/35 2/35 2/35 1/35
1/35 1/35 1/35 1/35 1/35
⊙高通濾波 空域高通濾波是對圖像的低頻分量進行擬制,讓圖像的高頻分量無損耗或者低損耗的通過。空域高通濾波常用的h(n1,n2)的如下:
0 -1 0
h(n1, n2) = -1 5 -1
0 -1 0
-1 -1 -1
h(n1, n2) = -1 9 -1
-1 -1 -1
1 -2 1
h(n1, n2) = -2 5 -2
0 -2 1
● 增強處理
⊙ 水平增強增強圖像水平方向線條也是一種高通濾波。水平增強的h(n1, n2)的例子如下:
0 0 0
h(n1, n2) = 0 0 0
-1 2 -1
⊙ 垂直增強增強圖像垂直方向線條也是一種高通濾波。水平增強的h(n1, n2)的例子如下:
-1 0 0
h(n1, n2) = 2 0 0
-1 0 0
⊙ 水平垂直增強水平垂直增強圖像也是一種高通濾波。水平增強的h(n1, n2)的例子如下:
-1 -1 -1
h(n1, n2) = -1 8 -1
-1 -1 -1
● 結構濾波
⊙ 並聯型結構濾波
結構如圖:
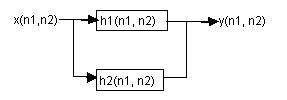
例如,當
0 0 0
h1(n1, n2) = 0 0 0
-1 2 -1
-1 0 0
h2(n1, n2) = 2 0 0
-1 0 0
則h(n1, n2)為
-1 0 0
h(n1, n2) = 2 0 0
-1 2 -1
⊙ 串聯型結構濾波
結構如圖:
![]()
例如,當
0 0 0
h1(n1, n2) = 0 0 0
-1 2 -1
-1 0 0
h2(n1, n2) = 2 0 0
-1 0 0
則h(n1, n2)為
1 -2 1
h(n1, n2) = -2 4 -2
1 -2 1
7) 圖象的切換特效處理
● 上部和下部對接顯示
只需要不斷的同時描繪對稱的上部和下部的一行像素即可
● 左部和右部對接顯示
只需要不斷的同時描繪對稱的左部和右部的一列像素即可
● 四邊向中央顯示
只需要不斷的同時等進階的描繪四邊直至描繪到中心點即可
● 中央向四邊顯示
只需要不斷的從中心點同時等進階的描繪四邊直至描繪到邊緣即可
● 四角向中心顯示
從左上角,右下角分別同時沿著主對角線等進階的描繪自己所在像素的行,列像素直至中心
● 水平刪條
設定分割長度L, 然後分別從高度為L, 2L, 3L ... 處等進階的描繪行像素,顯然這裡進階所需描繪高度為L
● 垂直刪條
設定分割長度L, 然後分別從寬度為L, 2L, 3L ... 處等進階的描繪列像素,顯然這裡進階所需描繪寬度為L
● 由左向右(由右向左)
分別從左至右(從右至左)不斷的描繪列像素直至邊緣
● 由上向下(由下向上)
分別由上向下(由下向上)不斷的描繪行像素直至邊緣
8) 邊緣探測
在圖像測量,模式識別時,從圖像中抽出線條,檢測出圖像邊緣或者抽出圖像輪廓是最常用的操作。迄今為止,已經出現了許多成熟的算法。例如微分算法,掩模算法等。在微分算法中,常使用N*N的像素塊,例如3*3或者4*4。3*3的像素塊如下,
f(i-1,j-1) f(i-1,j) f(i-1,j+1)
f(i,j-1) f(i,j) f(i,j+1)
f(i+1,j-1) f(i+1,j) f(i+1,j+1)
我們不妨設f(i,j)為待處理的像素,而g(i, j)為處理後的像素。
● Roberts算子
g(i, j) = sqrt( (f(i, j) - f(i + 1, j))^2 + (f(i + 1, j) - f(i, j + 1))^2 )
或者
g(i, j) = |f(i,j) - f(i + 1,j)| + |f(i+1,j) - f(i,j+1)|
● Sobel算子
對數字圖像的每一個像素f(i,j),考察它的上、下、左、右鄰域灰度的加權值,把各方向上(0度、45度、90度、135度)的灰度值加權之和作為輸出,可以達到提取圖像邊緣的效果。
即 g(i,j) = fxr + fyr, 其中
fxr = f(i-1,j-1)+2*f(i-1,j)+f(i-1,j+1)-f(i+1,j-1)-2*f(i+1,j)-f(i+1,j+1)
fyr = f(i-1,j-1)+2*f(i,j-1)+f(i+1,j-1)-f(i-1,j+1)-2*f(i,j+1)-f(i+1,j+1)
● Laplace算子
Laplace算子是一種二階微分算子。它有兩種形式:4鄰域微分算子和8鄰域微分算子。
⊙ 4鄰域微分
g(i,j)=|4*f(i,j)-f(i,j-1)-f(i-1,j)-f(i+1,j)-f(i,j+1)|
⊙ 8鄰域微分
g(i,j)=|8*f(i,j)-f(i,j-1)-f(i-1,j)-f(i+1,j)-f(i,j+1)-f(i-1,j-1)-f(i-1,j+1)-f(i+1,j-1)-f(i+1,j+1)|
● 其他常用算子
⊙ 右下邊緣抽出
采用3*3算子時,表達式為
g(i,j)=|-2*f(i,j-1)-2*f(i-1,j)+2*f(i+1,j)+2*f(i,j+1)|
⊙ prewitt 邊緣探測樣板算子
prewitt算子是一個邊緣模板算子,由八個方向的樣板組成,能夠在0度,45度,90度,135度,180度,225度角
等八個方向檢測邊緣。8個3*3邊緣模板及方向如下:
90度角: 45度角:
1 1 1 -1 -1 -1
1 -2 1 1 -2 1
-1 -1 -1 1 1 1
0度角: 315度角:
-1 1 1 1 1 -1
-1 -2 1 1 -2 -1
-1 1 1 1 1 -1
270度角: 225度角:
1 1 1 -1 -1 1
-1 -2 1 -1 -2 1
-1 -1 1 1 1 1
180度角: 135度角:
1 1 1 1 -1 -1
1 -2 -1 1 -2 -1
1 -1 -1 1 1 1
3*3時表達式如下:
A1*f(i-1,j-1) A8*f(i,j-1) A7*f(i+1,j-1)
A2*f(i-1,j) -2*f(i,j) A6*f(i+1, j)
A3*f(i-1,j+1) A4*f(i,j+1) A5*f(i+1,j+1)
g(i,j)=|-2*f(i,j)+A8*f(i,j-1)+A1*f(i-1,j-1)+A2*f(i-1,j)+A3*f(i-1,j+1)+A4*f(i,j+1)+A5*f(i+1,j+1)+A6*f(i+1,j)+A7*f(i+1,j-1)|
在程序設計中,依次用樣板去檢測圖像,與被檢測區域最為相似的樣板給出最大值,用該最大值作為算子的輸出值。
⊙ Robinson算子
Robinson算子是一個模板算子,由八個方向的樣板組成,能夠在0度,45度,90度,135度,180度,225度角
等八個方向檢測邊緣。8個3*3邊緣模板及方向如下:
90度角: 45度角:
1 2 1 0 1 2
0 0 0 -1 0 1
-1 -2 -1 -2 -1 0
0度角: 315度角:
-1 0 1 -2 -1 0
-2 0 2 -1 0 1
-1 0 1 0 1 2
270度角: 225度角:
-1 -2 -1 0 -1 -2
0 0 0 1 0 -1
1 2 1 2 1 0
180度角: 135度角:
1 0 -1 2 1 0
2 0 -2 1 0 -1
1 0 -1 0 -1 -2
使用方法與prewitt算子一樣。
⊙ Kirsch算子
Kirsch算子是一個模板算子,由八個方向的邊緣樣板組成,能夠在0度,45度,90度,135度,180度,225度角
等八個方向檢測邊緣。8個3*3邊緣模板及方向如下:
90度角: 45度角:
5 5 5 -3 5 5
-3 0 -3 -3 0 5
-3 -3 -3 -3 -3 -3
0度角: 315度角:
-3 -3 5 -3 -3 -3
-3 0 5 -3 0 5
-3 -3 5 -3 5 5
270度角: 225度角:
5 5 -3 -3 -3 -3
5 0 -3 5 0 -3
-3 -3 -3 5 5 -3
180度角: 135度角:
5 -3 -3 5 5 -3
5 0 -3 5 0 -3
5 -3 -3 -3 -3 3
使用方法與prewitt算子一樣。
⊙ Smoothed算子
Smoothed算子是一個3*3的算子,設
|-1 0 1| |1 1 1|
Dx = |-1 0 1| Dy = |0 0 0|
|-1 0 1| |-1 -1 -1|
則 D = sqrt(Dx^2 + Dy^2) 或者 D = |Dx| + |Dy|
或 Dx(i, j) = f(i-1,j+1)+f(i,j+1)+f(i+1,j+1)-f(i-1,j-1)-f(i,j-1)-f(i+1,j-1)
Dy(i,j) = f(i-1,j-1)+f(i-1,j)+f(i-1,j+1)-f(i+1,j-1)-f(i+1,j)-f(i+1,j+1)
9) 灰度圖像處理
所謂灰度處理是根據單色圖像的灰度對輸出圖像的灰度進行再定義、以改善圖像的對比度。單色圖像的灰度有256級、128級、64級等,下面均以256級單色圖像舉例。
我們不妨設源圖像的灰度值為f(i,j),處理後的灰度值為g(i,j)
● 逆反處理
與彩色圖像的逆反處理一樣: g(i,j) = 255 - f(i,j)
● 灰度級切換
灰度級切換的輸入、輸出灰度值對應關系如下:
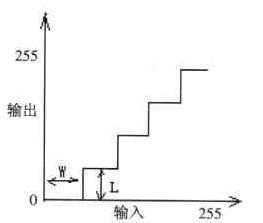
● 增大對比度
輸入的灰度值越高,對應的輸出灰度值越低。灰度值減少,圖像變暗,從而使對比度增加。
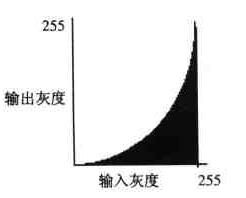
● 減小對比度
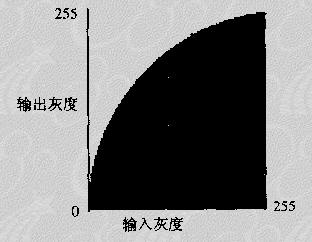
● 改善對比度
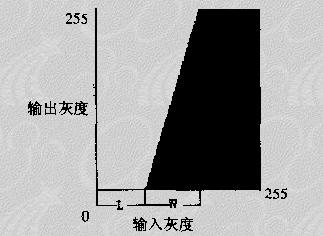
● 增強對比度
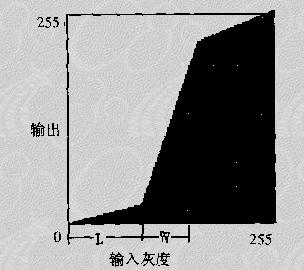
● 局部濾波處理
局部濾波處理是指利用3*3的圖像塊內的像素的顏色值對當前像素進行設定的一種圖像處理技術。
⊙ 平均值濾波
與彩色圖像平滑處理類似。
g(i,j)=( f(i-1,j-1) + f(i-1,j) + f(i-1,j+1) + f(i,j-1) + f(i,j) + f(i,j+1) + f(i+1,j-1) + f(i+1,j) + f(i+1,j+1) ) / 9
這裡要注意的是對於邊緣的像素的情況,防止越界。
⊙ 最小值濾波
最小值濾波是指在圖像中以當前像素f(i,j)為中心切出一個N*M(例如3*3)像素組成的圖像塊,g(i,j)取圖像塊中灰度值中的最小值
⊙ 最大值濾波
最大值濾波是指在圖像中以當前像素f(i,j)為中心切出一個N*M(例如3*3)像素組成的圖像塊,g(i,j)取圖像塊中灰度值中的最大值
⊙ 中值濾波
中值濾波是指在圖像中以當前像素f(i,j)為中心切出一個N*M(例如3*3)像素組成的圖像塊,g(i,j)取圖像塊中所有灰度排序後序列的中間值
10) 灰度圖像處理
● 灰度圖像的二值化
⊙ 灰度圖像直方圖
對於每個灰度值,求出在圖像中具有該灰度值的像素數的圖形叫做灰度直方圖。。灰度直方圖是灰度級的函數,描述圖像中具有相同灰度像素的個數。灰度直方圖的橫坐標是灰度級,縱坐標是該灰度出現的頻率(即像素的個數)。直方圖的用途主要是給出了一個簡單可見的指示,用來判斷一幅圖像是否合理的利用了全部被允許的灰度級范圍。一般一幅數字圖像應該利用全部或幾乎全部可能的灰度級范圍。一般一幅數字圖像應該利用全部或幾乎全部可能的灰度級,否則增加了量化間隔。一旦被數字化圖像的級數小於255,丟失的信息將不能恢復。如果圖像具有超出數字量化器所能處理的范圍的亮度,則這些灰度級將簡單的置為0或255,由此將在直方圖的一端或兩端產生尖峰。灰度圖像直方圖具有直方圖的一些統計特征參量,包括了灰度最大值,灰度最小值,均值和標准差。
⊙ 闕值計算和圖像二值化
圖像二值化的闕值處理方式為:
g(i,j) = 1; f(i,j)>=t
g(i,j) = 0; f(i,j)<t
通常,用g(i,j)=1表示圖像,用g(i,)=0表示背景。確定t的方法叫做闕值選擇。
● 灰度圖像的二值化算法
⊙ 類判別法尋找闕值的步驟:
(1) 計算輸入圖像的灰度級直方圖(用灰度級的概率函數PHS(i)來表示)
(2) 計算灰度均值(Ave) Ave = sigma((i - 1)*Phs(i)) i: 0->255
(3) 計算灰度類均值(Aver(k))和類直方圖和(W(k))
Aver(k) = sigma((i+1)*Phs(i)) i: 0->k
W(k) = sigma(Phs(i)) i: 1->k
(4)計算類分離指標
Q(k)={[Ave*W(k)-Aver(k)]^2)}/[W(k)*(1-W(k))]}
(5) 求使Q最大的k 最佳闕值: T = k - 1
⊙ 灰度級切片法
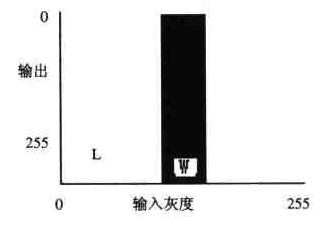
將輸入圖像的某一灰度級范圍內的所有像素全部置為0(黑),其余灰度級的所有像素全部置為255(白),則生成黑白
二值圖像。
⊙ 等灰度片二值化
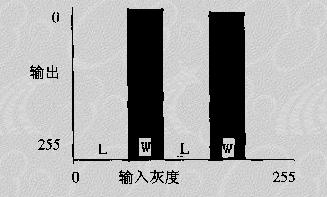
將輸入圖像在某兩個等寬的灰度級范圍內的所有像素全部置為0(黑),其余灰度級的所有像素全部置為255(白),則生成黑白二值圖像。
⊙ 線性二值化
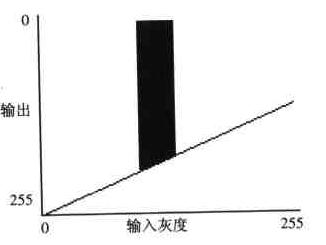
將輸入圖像在某一灰度級內的所有像素全部置為0(黑),其余灰度級的所有像素全部置為原值的1/2,則生成黑白二值圖像,並將圖像與背景分離。
● 二值圖像處理
二值圖像處理是指將二值化的圖像進行某種修正,使之更適合於圖像測量。二值圖像處理包括以下操作:
膨脹 使粒子變大。對圖像進行膨脹處理之後再進行收縮處理,則可以修正圖像的凹槽
收縮 使粒子變小。對圖像進行收縮處理之後再進行膨脹處理,則可以修正圖像的凸槽
清除孤立點 清除由一個像素構成的對象以及修正由一個像素構成的孔。
清除粒子 清除任意面積以下的對象
清除超大粒子 清除任意面積以上的對象
洞穴填充 填充任意范圍
⊙ 4鄰域收縮
4鄰域收縮的原理是,在3*3的圖像塊中,如果當前處理像素f(i,j)為0,則其相鄰的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j)均置255。
⊙ 8鄰域收縮
8鄰域收縮的原理是,在3*3的圖像塊中,如果當前處理像素f(i,j)為0,則其相鄰的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j),f(i-1,j-1),f(i+1,j-1),f(i-1,j+1),f(i+1,j+1)均置255。
⊙ 4鄰域膨脹
4鄰域膨脹的原理是,在3*3的圖像塊中,如果當前處理像素f(i,j)為1,則其相鄰的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j)均置1。
⊙ 8鄰域膨脹
8鄰域膨脹的原理是,在3*3的圖像塊中,如果當前處理像素f(i,j)為1,則其相鄰的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j),f(i-1,j-1),f(i+1,j-1),f(i-1,j+1),f(i+1,j+1)均置1。
⊙ 8鄰域清除孤立點
8鄰域清除孤立點的原理是,在3*3的圖像塊中,如果當前處理像素f(i,j)為1,而其相鄰的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j),f(i-1,j-1),f(i+1,j-1),f(i-1,j+1),f(i+1,j+1)均為0時,當前處理像素f(i,j)為0。
⊙ 4鄰域清除孤立點
4鄰域清除孤立點的原理是,在3*3的圖像塊中,如果當前處理像素f(i,j)為1,而其相鄰的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j均為0時,當前處理像素f(i,j)為0。
这篇关于圖像處理算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







