教你使用几种常用的等概率抽样法

在统计建模过程中往往会使用到采样技术，通过样本来反映总体特征。关于采样，目前主要有两大类抽样技术，即等概率抽样和非等概率抽样，而在实际应用中，等概率抽样是最常见的，下面就讲讲等概率抽样中的几种抽样技术。

一、简单随机抽样

简单随机抽样(SRS)是我们经常接触到的抽样方法，比如摸彩或抽奖，或办公室需要有人出公差去送数据时用抽签决定人选。SRS的特色是母群体中的每一个体都有相同的机会被选中进入样本，这是一种最公平且概念上最简单的抽样法，可以直接套用统计学原理去进行估算与推论。关于简单随机抽样，在R中可以使用自带的sample()函数实现，下面是sample()函数的语法及参数意义：

sample(x, size, replace = FALSE, prob = NULL)

x：抽样对象，为一个向量

size：抽样规模，即需要从总体x中抽取多少样本

replace：指定是否有放回的抽样，默认为无放回，当设置为TRUE时，则表示简单随机抽样是有放回的

prob：指定抽样元素的概率，默认是每个个体被等概率抽中

例子：

```{r}

#向量--无放回

values <- runif(100, min = 10, max = 100)

sample1 <- sample(values, size = 10, replace = FALSE)

sample1

#向量--有放回,不等概率

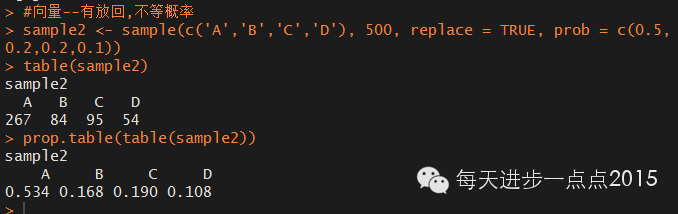
sample2 <- sample(c('A','B','C','D'), 500, replace = TRUE, prob = c(0.5,0.2,0.2,0.1))

table(sample2)

prop.table(table(sample2))

#数据框

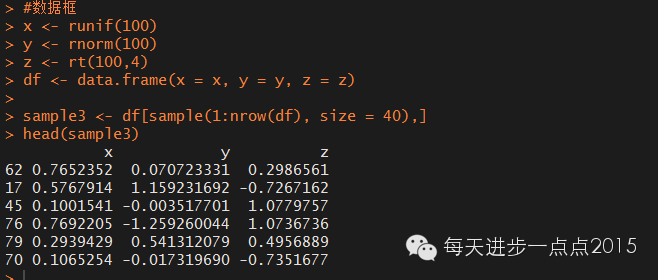
x <- runif(100)

y <- rnorm(100)

z <- rt(100,4)

df <- data.frame(x = x, y = y, z = z)

sample3 <- df[sample(1:nrow(df), size = 40),]

head(sample3)

```

二、系统抽样

系统抽样方法是一种简化的随机抽样法，最普遍的做法是从母群体的名单中，按照一定的间隔取出足够的个体组成样本。比如我们可以从这500家医院的名单中，每10间医院取一间来做为样本个体。但首先我们必须先随机决定一个起始的号码，也就是从1-10之间随机选出一个号码，假如选中的是3号，则我们从3号开始，每10号取一家医院做为样本(3, 13, 23, 33,…493)。关于系统抽样，在R中可以使用sampling包中的UPsystematic()函数实现，下面是UPsystematic()函数的语法及参数意义：

UPsystematic(pik,eps=1e-6)

pik：为一向量，存放抽样的包含概率

esp：为一控制值，默认为1e-6

例子：

```{r}

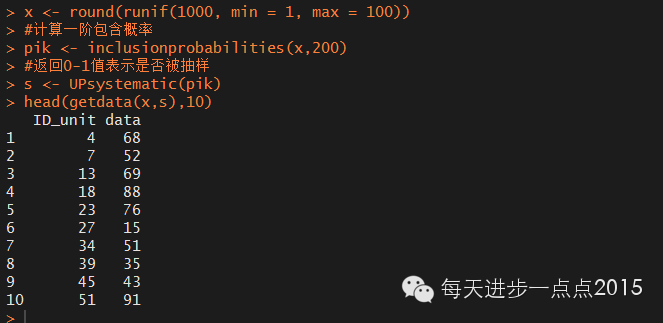
x <- round(runif(1000, min = 1, max = 100))

#计算一阶包含概率

pik <- inclusionprobabilities(x,200)

#返回0-1值表示是否被抽样

s <- UPsystematic(pik) 

head(getdata(x,s),10)

```

但从上面的返回的ID_unit看，并不是系统抽样定义的那样，即等间隔的抽取样本。为保证与定义一致，这里自定义系统抽样的函数：

```{r}

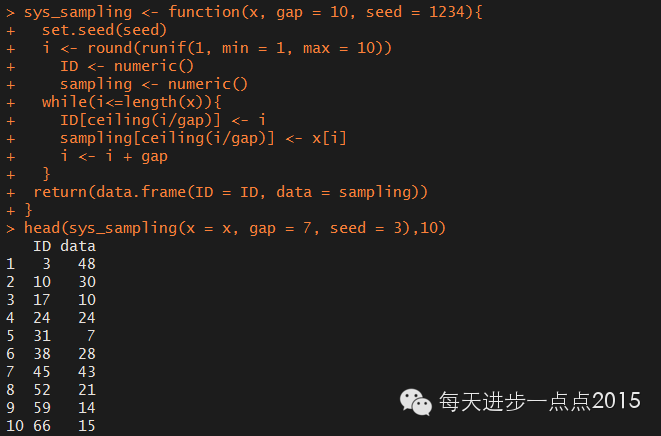
sys_sampling <- function(x, gap = 10, seed = 1234){

  set.seed(seed)

  i <- round(runif(1, min = 1, max = 10))

    ID <- numeric()

    sampling <- numeric()

  while(i<=length(x)){

    ID[ceiling(i/gap)] <- i

    sampling[ceiling(i/gap)] <- x[i]

    i <- i + gap

  }

 return(data.frame(ID = ID, data = sampling))   

}

```

其中，x为待抽样的总体；gap为抽样间隔，默认为10；seed为种子数，用于从[1,10]之间随机挑选一个起始号设定随机种子，默认为1234。

例子：

```{r}

head(sys_sampling(x = x, gap = 7, seed = 3),10)

```

三、分层抽样

分层或分组抽样是一种比SRS更精准的随机抽样法，所用的方法是跟据我们的研究性质，依照相关的条件把母群体中的个体分成不同的层别或组别(strata)，再分别从每一层别或组别中的个体随机抽出一定的个体来组成样本。在R中可以使用sampling包中的strata()函数实现，下面是strata()函数的语法及参数意义：

strata(data, stratanames=NULL, size, 

          method=c("srswor","srswr","poisson","systematic"), 

          pik,description=FALSE)

data：待抽样的数据框

stratanames：指定数据框中的分层变量

size：指定每个层中的抽样数量，默认按原数据中分层变量水平的顺序指定抽样数量

method：指定抽取各层数据的方法，默认为无放回的简单随机抽样，还可以是有放回的简单随机抽样、泊松抽样和系统抽样

pik：如果选择系统抽样时，需要指定系统抽样的包含概率pik向量

例子：

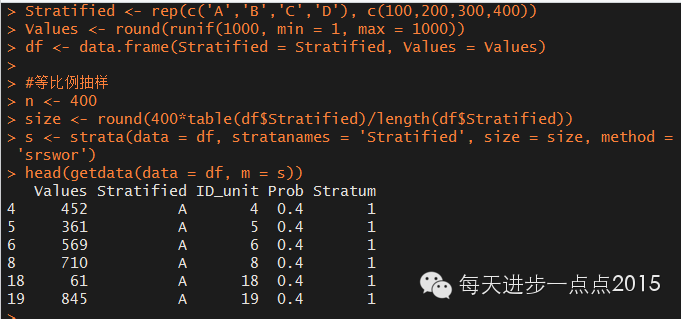
```{r}

Stratified <- rep(c('A','B','C','D'), c(100,200,300,400))

Values <- round(runif(1000, min = 1, max = 1000))

df <- data.frame(Stratified = Stratified, Values = Values)

#等比例抽样

n <- 400

size <- round(400*table(df$Stratified)/length(df$Stratified))

s <- strata(data = df, stratanames = 'Stratified', size = size, method = 'srswor')

head(getdata(data = df, m = s))

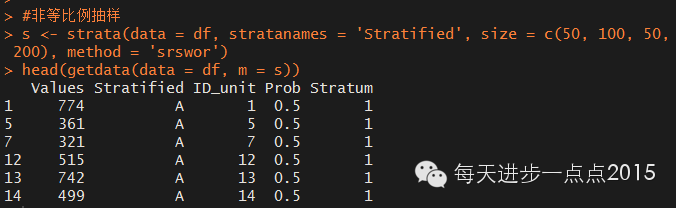
#非等比例抽样，随意指定抽样数量

s <- strata(data = df, stratanames = 'Stratified', size = c(50, 100, 50, 200), method = 'srswor')

head(getdata(data = df, m = s))

```

四、聚集抽样

聚集抽样也是跟据某种母群体的特性，将母群体中的个体分成不同的群组(clusters)，然后从这些群组中随机抽出部分的群组，再从被选中的群组中随机抽出足够的个体来组成样本。

从定义上看，聚集抽样与分层抽样很相似，但各自的组是完全两回事。在聚集抽样中，尽量保证组内数据差异特别大，而组间差异尽量小；在分层抽样中就恰恰相反，即组内差异尽量小，而组间差异要求很大。在R中可以使用sampling包中的cluster()函数实现，下面是cluster()函数的语法及参数意义：

cluster(data, clustername, size, 

           method=c("srswor","srswr","poisson","systematic"),

           pik,description=FALSE)

data：待抽样的数据框

clustername：指定数据框中的聚集变量

size：指定抽取多少个组

method：指定抽取的方法，默认为无放回的简单随机抽样，还可以是有放回的简单随机抽样、泊松抽样和系统抽样

pik：如果选择系统抽样时，需要指定系统抽样的包含概率pik向量

例子：

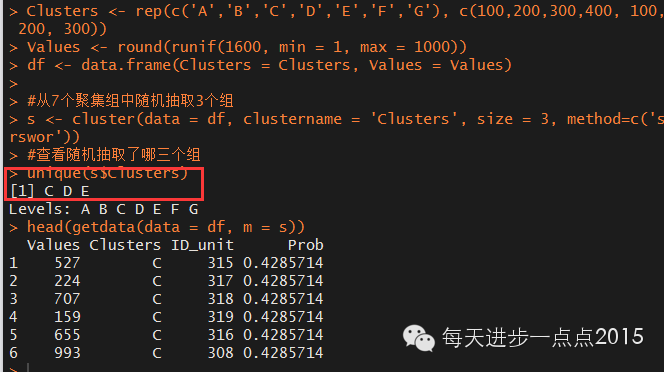
```{r}

Clusters <- rep(c('A','B','C','D','E','F','G'), c(100,200,300,400, 100, 200, 300))

Values <- round(runif(1600, min = 1, max = 1000))

df <- data.frame(Clusters = Clusters, Values = Values)

#从7个聚集组中随机抽取3个组

s <- cluster(data = df, clustername = 'Clusters', size = 3, method=c('srswor'))

#查看随机抽取了哪三个组

unique(s$Clusters)

head(getdata(data = df, m = s))

```

参考资料

https://www.douban.com/group/topic/72819666/

每天进步一点点2015

学习与分享，取长补短，关注小号！

     长按识别二维码à马上关注