深度学习_GAN_CycleGAN

本文主要是介绍深度学习_GAN_CycleGAN，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

非匹配数据的图像转换

Pix2Pix可以很好地处理匹配数据集的图像转换，但是在很多情况下匹配数据集是没有的或者说非常难收集到。在实际生活中，我们却可以很容易的拿到两个领域的大量非匹配数据。

下图展示了匹配数据和非匹配数据的区别：

CycleGAN就是解决非匹配数据集的图像转换的一种非常好用的网络。对于照片风格的转换，传统CNN网络是通过将某个画作中的风格叠加到原始图片上，如下图所示：

上面的方法仅仅将两张特定的图片之间进行转换，而CycleGAN的转换是存在于两个图像领域中的。

接下来我们欣赏一下一些CycleGAN转换的例子，在学习技术的同时也感受艺术的魅力。
以下，enjoy：

CycleGAN框架

CycleGAN的核心架构是由两个生成对抗网络的合作组成的。X与Y分别代表两组不同领域的图像数据，第一组生成对抗网络是生成器G（从X到Y的生成）与判别器$D_Y$，用于判断图像是否属于领域Y；第二组生成对抗网络是反向的生成器F（从Y到X的生成）与判别器$D_X$，用于判断图像是否属于领域X。两个生成器G和F的目标都是尽可能生成对方领域中的图像以“骗过”各自对应的判别器$D_Y$和$D_X$。

CycleGAN逻辑结构

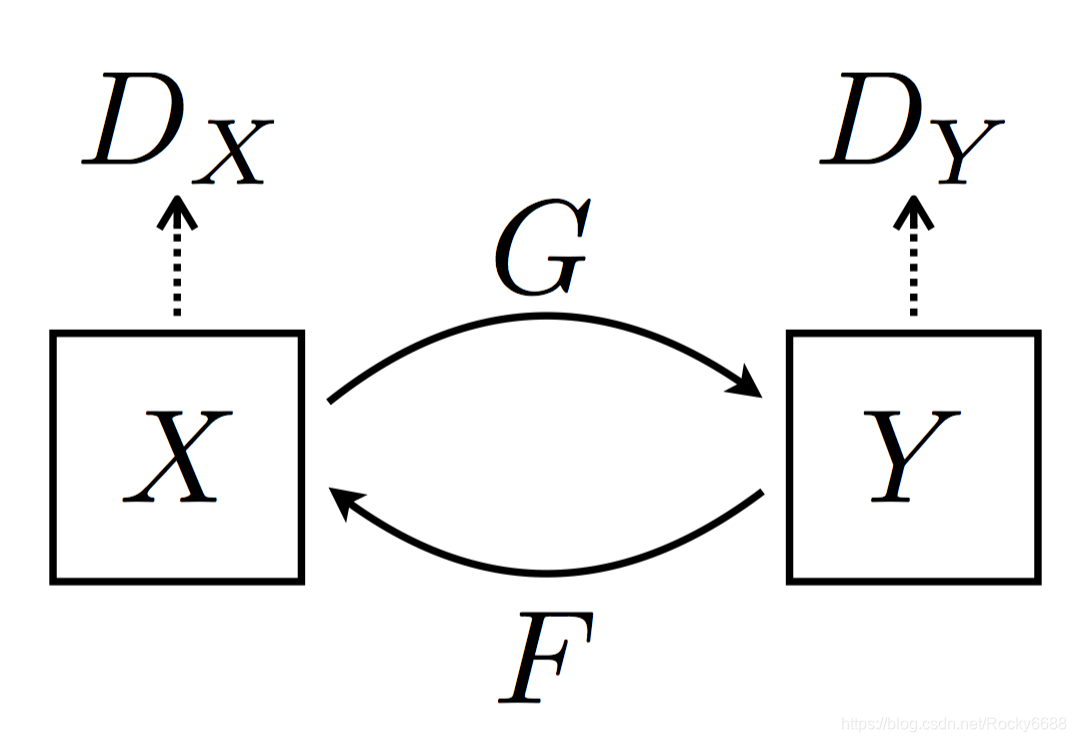
生成器结构

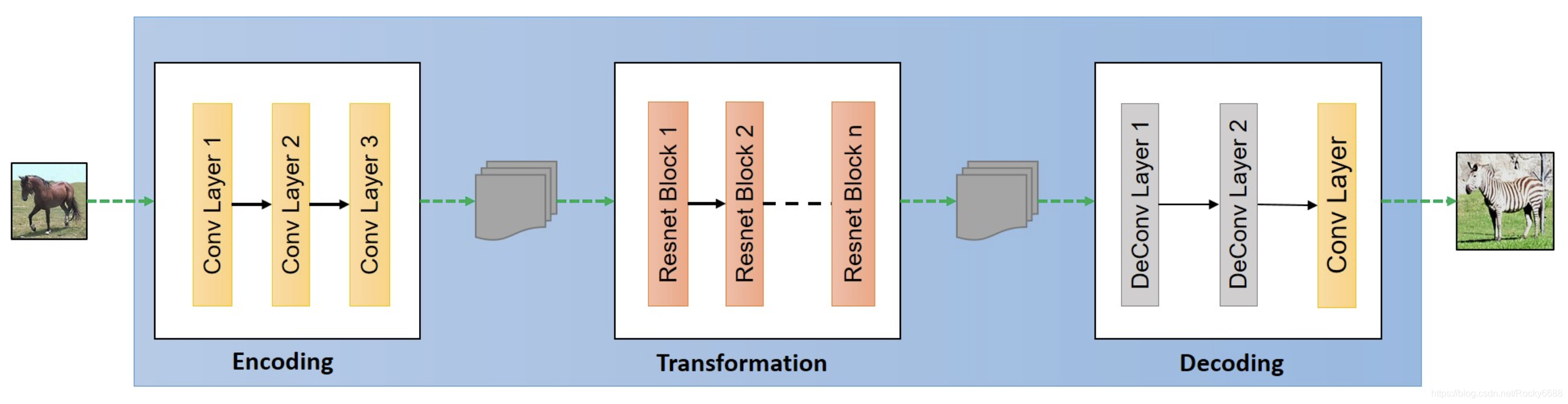
由编码层、转换层和解码层三部分组成。

判别器结构

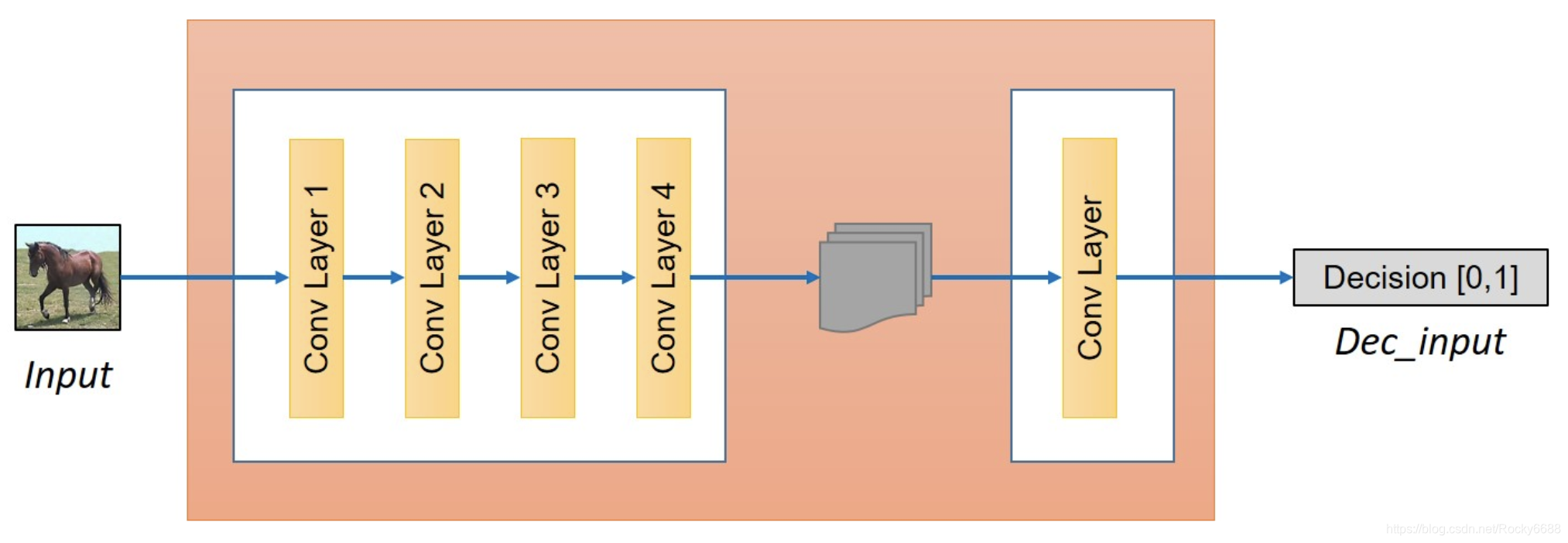
CycleGAN目标函数

CycleGAN中引入了Cycle-consistency Loss。我们需要将两组生成对抗网络有机地结合起来。我们首先看下面第一张图，在生成器G通过条件数据x生成Y领域的数据$\hat{Y}$后，我们需要将它通过对面的生成器F重新还原一个原来领域中的$\hat{x}$，为了保证一致性，我们希望让x和$\hat{x}$尽可能接近，而x和$\hat{x}$之间的距离我们称之为Cycle-consistency Loss。

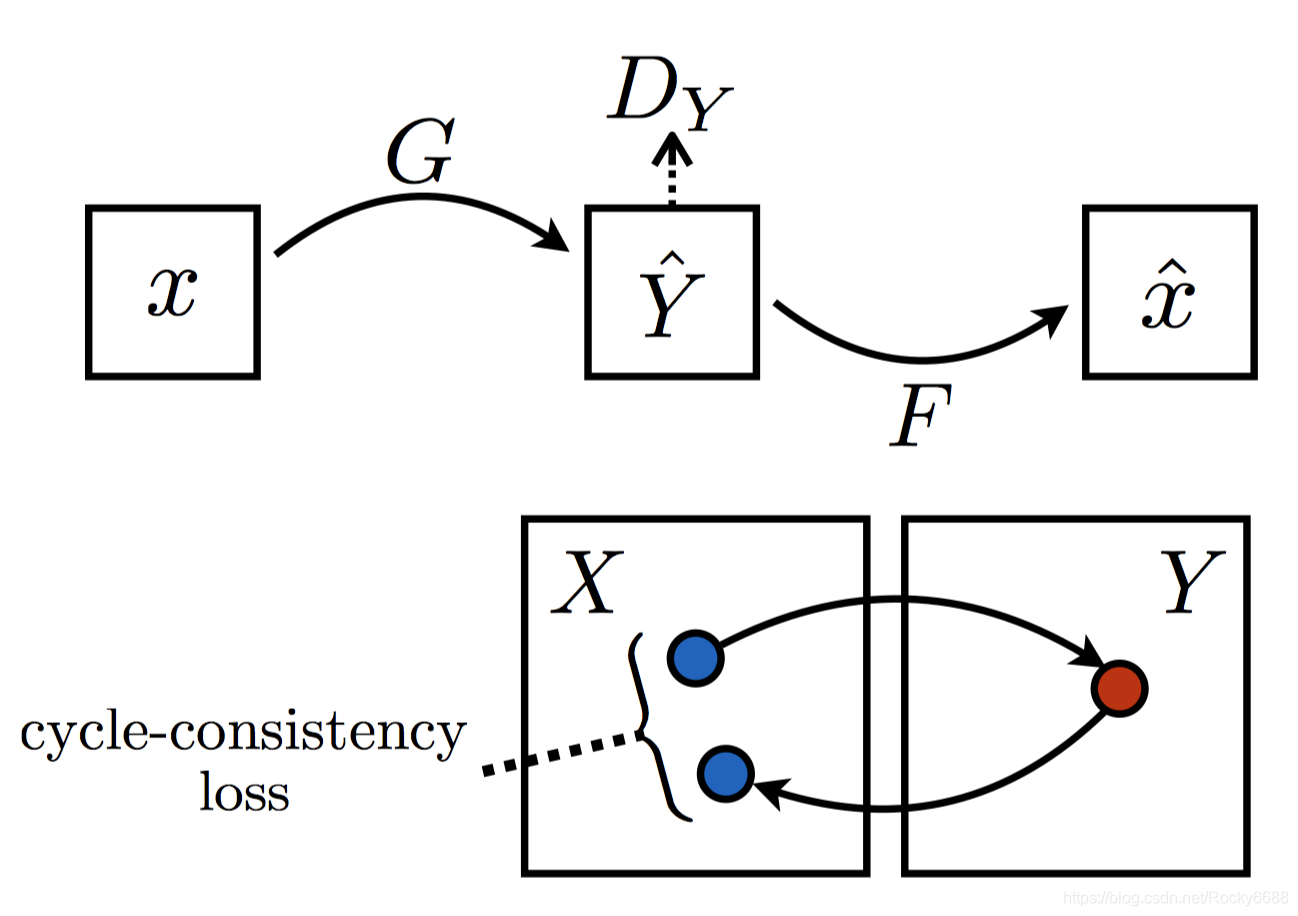
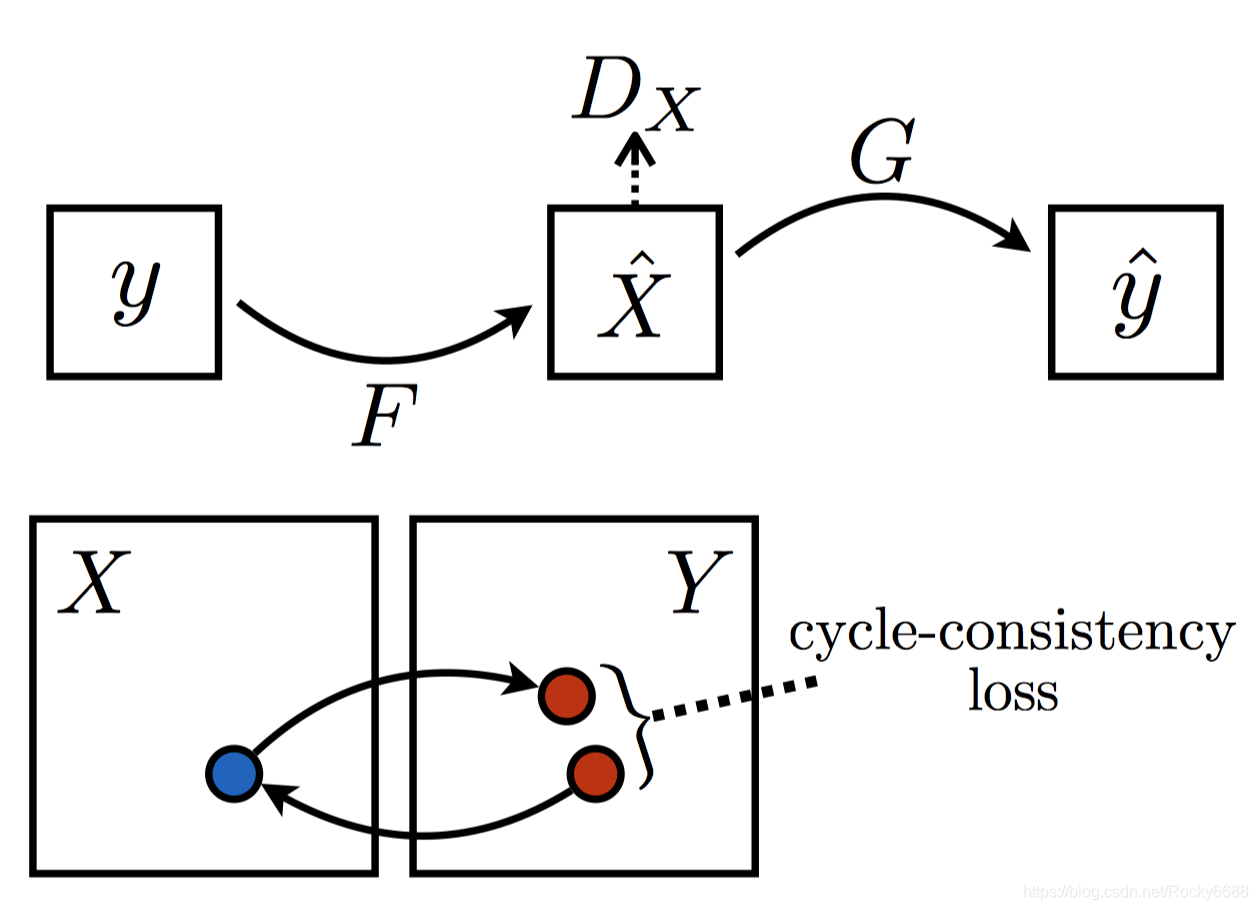
上面的两个图可以有下面的两个公式概括：

$$x\to G(x)\to F(G(x))\approx x$$

$$y\to F(y)\to G(F(y))\approx y$$

接下来我们需要设计两个对抗网络的对抗损失：

$$L_{GAN}(G,D_Y,X,Y)={\mathrm{E}}_{y\sim p_{data}(y)}[\log D_Y(y)]+{\mathrm{E}}_{x\sim p_{data}(x)}[\log (1-D_Y(G(x))]$$

$$L_{GAN}(G,D_X,X,Y)={\mathrm{E}}_{x\sim p_{data}(x)}[\log D_X(x)]+{\mathrm{E}}_{y\sim p_{data}(y)}[\log (1-D_X(F(y))]$$

接下来我们定义Cycle-consistency Loss来确保生成器产生的数据能够与反向生成后的数据基本保持一致。

$$L_{cyc}(G,F)={\mathrm{E}}_{x\sim p_{data}x}[||F(G(x))-x|{|}_1]+{\mathrm{E}}_{y\sim p_{data}y}[||G(F(x))-y|{|}_1]$$

最后我们可以得出完整的目标函数：

$$L(G,F,D_X,D_Y)=L_{GAN}(G,D_Y,X,Y)+L_{GAN}(F,D_X,Y,X)+\lambda L_{cyc}(G,F)$$

与原始GAN一样，最终的优化函数依然是需要解决下面的这个极小极大值问题：

$$G^{\ast },F^{\ast }=\underset{G,F}{\min }\underset{D_X,D_Y}{\max }L(G,F,D_X,D_Y)$$

实验

这篇关于深度学习_GAN_CycleGAN的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---