最小体力消耗路径（算法）

最小体力消耗路径（算法）

题目描述

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

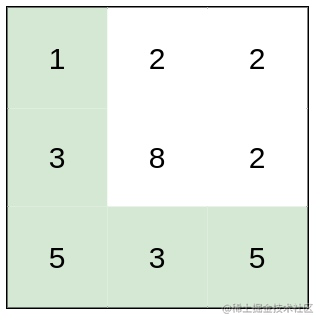
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

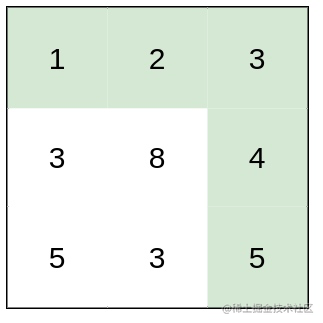
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

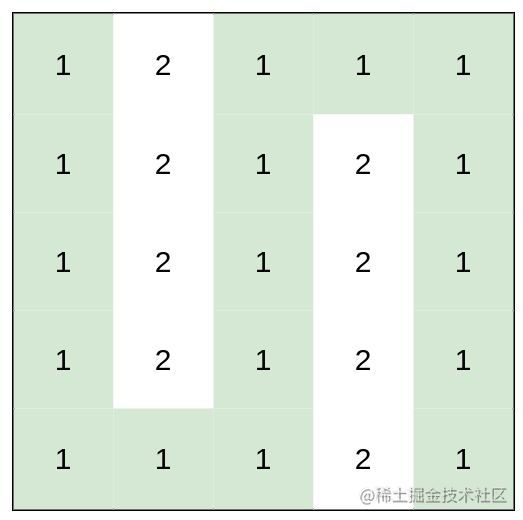
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

思路分析一

最开始想用动态规划思路看看能不能解决问题，但是该题可以有四个方向移动，并不是每次都只能往下或者往右移动，dp解决不了该题

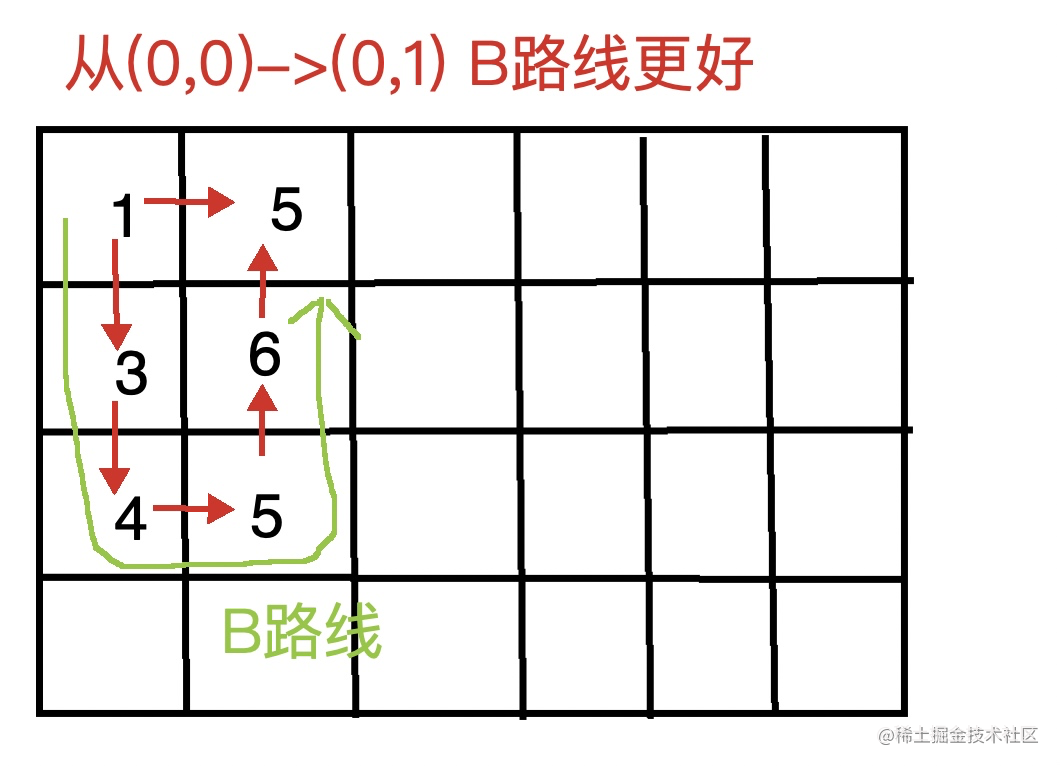
上述的例子证明了路线的选择是变化多端的，但是也引入了我的一个思考：
第一步怎么走，是从(0,0)->(0,1)还是从（0,0）->(1,0)
显然走绝对值最小的那样一个

因此现在我们已经从（0，0）走到了（1，0），变化就是我们多了一个格子，以及多了两种选择即（1，0)->(1,1),（1，0)->(2,0)

也就是说我们维护一个优先队列，每次选取最少的路线去走，就能得到当下最好的结果

随着边不断的加入队列以及被遍历，我们只要找到终点就行啦

最后暮然回首发现思想很想Djstla算法。

思路分析二

我们可以想象一下，绝对值差的越多的地方像凸起的岛屿，而这个矩阵上方在均匀的下雨，下面雨水什么时候可以吧（0，0）以及（n-1，m-1）联通在一起呢？

很明显也可以用并查集的思想解决此问题

我们设置消耗最大体力max为0，随着max的不断提升，我们就可以从一个方格移动到另一个方格之中，这些方格是联通的

知道max大到一定程度，（0，0）所在的方格也和（n-1，n-1）的方格联通即可，就是我们寻找的max

怎么转化为程序语言呢，同样可以维护一个最小堆，让所有边都进入堆中，从最小的开始不断的联通矩阵即可。如果左上角和右下角从非连通状态变为连通状态，那么这个边的长度即为答案。

最短路径Code

class Solution {int[] dis1=new int[]{1,-1,0,0};int[] dis2=new int[]{0,0,1,-1};PriorityQueue<Integer[]>queue;int max;boolean[][] array;int[][] heights;public int minimumEffortPath(int[][] heights) {queue=new PriorityQueue<>(new Comparator<Integer[]>() {@Overridepublic int compare(Integer[] o1, Integer[] o2) {return o1[0]-o2[0];}});max=0;this.heights=heights;array=new boolean[heights.length][heights[0].length];array[0][0]=true;if(array.length>1)queue.add(new Integer[]{Math.abs(heights[1][0]-heights[0][0]),1,0});if(array[0].length>1) queue.add(new Integer[]{Math.abs(heights[0][1]-heights[0][0]),0,1});while (queue.isEmpty()==false){Integer[] temp=queue.poll();max=Math.max(max,temp[0]);int curx=temp[1];int cury=temp[2];array[curx][cury]=true;if(curx==array.length-1&&cury==array[0].length-1)return max;for (int i = 0; i < dis1.length; i++) {if(curx+dis1[i]>=0&&curx+dis1[i]<heights.length&&cury+dis2[i]>=0&&cury+dis2[i]<heights[0].length){if(array[curx+dis1[i]][cury+dis2[i]])continue;queue.add(new Integer[]{Math.abs(heights[curx][cury]-heights[curx+dis1[i]][cury+dis2[i]]),curx+dis1[i],cury+dis2[i]});}}}return 0;}}

并查集Code

可以从合并的size中进行优化

    int[] dis1=new int[]{1,-1,0,0};int[] dis2=new int[]{0,0,1,-1};PriorityQueue<Integer[]>queue;int[][] father;int target;public int minimumEffortPath(int[][] heights) {father=new int[heights.length][heights[0].length];target=(heights.length-1)*1000+heights[0].length-1;queue=new PriorityQueue<>(new Comparator<Integer[]>() {@Overridepublic int compare(Integer[] o1, Integer[] o2) {return o1[0]-o2[0];}});for (int i = 0; i < heights.length; i++) {for (int j = 1; j < heights[0].length; j++) {queue.add(new Integer[]{Math.abs(heights[i][j]-heights[i][j-1]),i,j,i,j-1});}}for (int i = 0; i < heights[0].length; i++) {for (int j = 1; j < heights.length; j++) {queue.add(new Integer[]{Math.abs(heights[j-1][i]-heights[j][i]),j-1,i,j,i});}}for (int i = 0; i < heights.length; i++) {for (int j = 0; j < heights[0].length; j++) {father[i][j]=-1;}}father[0][0]=0;father[heights.length-1][heights[0].length-1]=(heights.length-1)*1000+heights[0].length-1;while (queue.isEmpty()==false){Integer[] temp=queue.poll();int max=temp[0];int f1=getFather(temp[1],temp[2]);int f2=getFather(temp[3],temp[4]);if(f1==f2)continue;if(f1==0&&f2==target||f1==target&&f2==0)return max;merge(f1,f2);}return 0;}public void merge(int f1,int f2){if(f2==0||f2==target) {father[f1/1000][f1%1000]=f2;}else{father[f2/1000][f2%1000]=f1;}}public int getFather(int x,int y){int temp=father[x][y];if(temp==-1)return x*1000+y;if(temp== x*1000+y)return temp;return getFather(temp/1000,temp%1000);}