算法练习帖--66--最小体力消耗路径(Java)

2023-10-11 20:30
文章标签 java 算法 路径 最小 练习 66 消耗 体力

本文主要是介绍算法练习帖--66--最小体力消耗路径(Java)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最小体力消耗路径(Java)

一、题目简介

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。
(题目来源：力扣（LeetCode）)
示例 1：
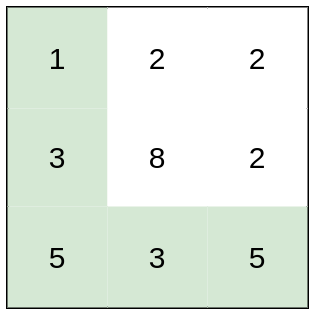
在这里插入图片描述

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：
在这里插入图片描述

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：
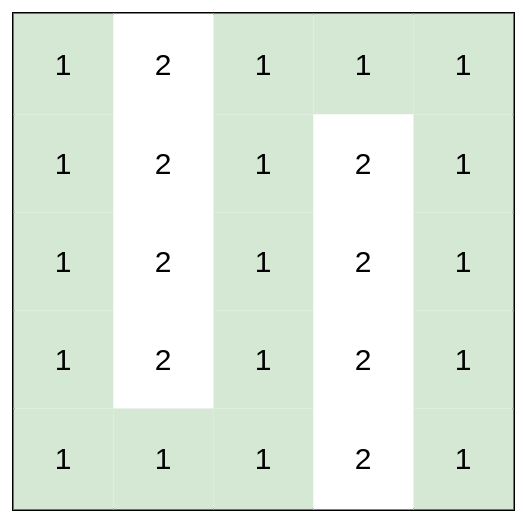
在这里插入图片描述

输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106
二、解决方法

1. 二分+bfs(官方题解)

package com.lxf.test3;import java.util.LinkedList;
import java.util.Queue;class Solution {int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};public int minimumEffortPath(int[][] heights) {int m = heights.length;//行数int n = heights[0].length;//列数//因为1=<heights[i][j]<=1000000,所以体力消耗值最小值在0-999999中//所以我们在这区间二分查找就可以了int left = 0, right = 999999, ans = 0;while (left <= right) {//当left==right时，left和right和mid都是最小体力消耗值int mid = (left + right) / 2;//取中间值Queue<int[]> queue = new LinkedList<int[]>();//加入初始点queue.offer(new int[]{0, 0});//记录当前顶点是否被访问boolean[] seen = new boolean[m * n];seen[0] = true;//bfs遍历整张图，把体力消耗值<=mid的全部走一边while (!queue.isEmpty()) {int[] cell = queue.poll();//取出当前点坐标int x = cell[0], y = cell[1];for (int i = 0; i < 4; ++i) {//将当前顶点的上下左右顶点遍历int nx = x + dirs[i][0];int ny = y + dirs[i][1];//如果上下左右顶点没越界，并且体力消耗值<=mid//我们就走这个点，并标志为已访问过if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && Math.abs(heights[x][y] - heights[nx][ny]) <= mid) {queue.offer(new int[]{nx, ny});seen[nx * n + ny] = true;}}}//遍历完图之后判断最后一个顶点访问过没有if (seen[m * n - 1]) {//访问到了，说明最小体力消耗值在当前区间mid中点的左区间ans = mid;right = mid - 1;} else {//没有访问到了，说明最小体力消耗值在当前区间mid中点的右区间left = mid + 1;}}return ans;}
}

2. 并查集+克鲁斯卡尔算法（参照官方题解）

package com.lxf.bfs;import java.util.PriorityQueue;public class MinimumEffortPath {public static void main(String[] args) {MinimumEffortPath m = new MinimumEffortPath();m.minimumEffortPath(new int[][]{{1,2,2},{3,8,2},{5,3,5}});}int[] parent;int[] rank;public int minimumEffortPath(int[][] heights) {int row=heights.length;int col=heights[0].length;parent=new int[row*col];//父结点数组rank=new int[row*col];//秩结点数组//数组存储两个结点和两结点的权值，并用小根堆存储PriorityQueue<int[]> pq = new PriorityQueue<>((arr1, arr2) -> arr1[2] - arr2[2]);for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {//二维数组一维化int index=i*col+j;parent[index]=index;//父结点数组初始化//将当前结点的上和左结点移动到当前结点的体力值记录到数组中，并存储到小根堆if(i>0){pq.offer(new int[]{index-col,index,Math.abs(heights[i][j]-heights[i-1][j])});}if(j>0){pq.offer(new int[]{index-1,index,Math.abs(heights[i][j]-heights[i][j-1])});}}}int min=0;//最小体力值while(!pq.isEmpty()){//依次取出小根堆中的值，也就是已经从体力值最小一直取int[] nums = pq.poll();//合并结点union(nums[0],nums[1]);if(find(0)==find(row*col-1)){//如果开始结点和最后结点相通，说明已经连通了，当前体力值就是最小花费体力值min=nums[2];break;}}return min;}/*** 查找父结点方法* @param index* @return*/public int find(int index){while(index!=parent[index]){parent[index]=parent[parent[index]];index=parent[index];}return index;}/*** 合并集合方法* @param index1* @param index2*/public void union(int index1,int index2){int root1=find(index1);int root2=find(index2);if(root1==root2){return;}if(rank[root1]>rank[root2]){parent[root2]=root1;}else if(rank[root1]<rank[root2]){parent[root1]=root2;}else{parent[root2]=root1;rank[root1]++;}}
}

3. 迪杰斯特拉算法(官方题解)

package com.lxf.dijstra;import java.util.Arrays;
import java.util.PriorityQueue;public class MinimumEffortPath {//方向计算数组：上右下左int[][] dirs=new int[][]{{-1,0},{0,1},{1,0},{0,-1}};public int minimumEffortPath(int[][] heights) {int row=heights.length;//heights数组行int col=heights[0].length;//heights数组列int length=row*col;//heights数组用一维数组存储的长度//存储从(0,0)顶点到当前顶点所需要花费的最小体力值数组int[] dists = new int[length];//设置数组初始值为int的最大值Arrays.fill(dists,Integer.MAX_VALUE);//设置起点最小体力值为0dists[0]=0;//记录顶点是否访问过的数组boolean[] visited = new boolean[length];//存储边的优先队列PriorityQueue<int[]> pq = new PriorityQueue<>((arr1, arr2) -> arr1[2] - arr2[2]);pq.offer(new int[]{0,0,0});//添加起始数组while (!pq.isEmpty()) {int[] poll = pq.poll();int x = poll[0], y = poll[1], d = poll[2];//当前顶点的一维坐标int index=x*col+y;if(visited[index]){//如果当前顶点已经访问过，直接取下一个顶点continue;}visited[index]=true;//标记当前下标已被访问if(index==length-1){//如果到达了最后顶点，直接跳出循环break;}for (int i = 0; i < dirs.length; i++) {int nx=x+dirs[i][0];int ny=y+dirs[i][1];if(nx>=0&&ny>=0&&nx<row&&ny<col&&Math.max(d,Math.abs(heights[nx][ny]-heights[x][y]))<dists[nx*col+ny]){//当向上右下左走一个顶点，并且走完这个顶点花费的体力值要比其它路径花费的小//更新结点的体力值，并将结点加入队列dists[nx*col+ny]=Math.max(d,Math.abs(heights[nx][ny]-heights[x][y]));pq.offer(new int[]{nx,ny,dists[nx*col+ny]});}}}return dists[length-1];}
}

这篇关于算法练习帖--66--最小体力消耗路径(Java)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/190645。

相关文章

JVM 的类初始化机制

JVM 的类初始化机制

前言 当你在 Java 程序中new对象时，有没有考虑过 JVM 是如何把静态的字节码（byte code）转化为运行时对象的呢，这个问题看似简单，但清楚的同学相信也不会太多，这篇文章首先介绍 JVM 类初始化的机制，然后给出几个易出错的实例来分析，帮助大家更好理解这个知识点。 JVM 将字节码转化为运行时对象分为三个阶段，分别是：loading 、Linking、initialization
阅读更多...
Spring Security 基于表达式的权限控制

Spring Security 基于表达式的权限控制

前言 spring security 3.0已经可以使用spring el表达式来控制授权，允许在表达式中使用复杂的布尔逻辑来控制访问的权限。 常见的表达式 Spring Security可用表达式对象的基类是SecurityExpressionRoot。 表达式描述hasRole([role])用户拥有制定的角色时返回true （Spring security默认会带有ROLE_前缀）,去
阅读更多...
浅析Spring Security认证过程

浅析Spring Security认证过程

类图 为了方便理解Spring Security认证流程，特意画了如下的类图，包含相关的核心认证类 概述 核心验证器 AuthenticationManager 该对象提供了认证方法的入口，接收一个Authentiaton对象作为参数; public interface AuthenticationManager {Authentication authenticate(Authenti
阅读更多...
Spring Security--Architecture Overview

Spring Security--Architecture Overview

1 核心组件 这一节主要介绍一些在Spring Security中常见且核心的Java类，它们之间的依赖，构建起了整个框架。想要理解整个架构，最起码得对这些类眼熟。 1.1 SecurityContextHolder SecurityContextHolder用于存储安全上下文（security context）的信息。当前操作的用户是谁，该用户是否已经被认证，他拥有哪些角色权限…这些都被保
阅读更多...
Spring Security基于数据库验证流程详解

Spring Security基于数据库验证流程详解

Spring Security 校验流程图 相关解释说明（认真看哦） AbstractAuthenticationProcessingFilter 抽象类 /*** 调用 #requiresAuthentication(HttpServletRequest, HttpServletResponse) 决定是否需要进行验证操作。* 如果需要验证，则会调用 #attemptAuthentica
阅读更多...
Spring Security 从入门到进阶系列教程

Spring Security 从入门到进阶系列教程

Spring Security 入门系列 《保护 Web 应用的安全》 《Spring-Security-入门（一）：登录与退出》 《Spring-Security-入门（二）：基于数据库验证》 《Spring-Security-入门（三）：密码加密》 《Spring-Security-入门（四）：自定义-Filter》 《Spring-Security-入门（五）：在 Sprin
阅读更多...
Java架构师知识体认识

Java架构师知识体认识

源码分析 常用设计模式 Proxy代理模式Factory工厂模式Singleton单例模式Delegate委派模式Strategy策略模式Prototype原型模式Template模板模式 Spring5 beans 接口实例化代理Bean操作 Context Ioc容器设计原理及高级特性Aop设计原理Factorybean与Beanfactory Transaction 声明式事物
阅读更多...
不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
Java进阶13讲__第12讲_1/2

Java进阶13讲__第12讲_1/2

多线程、线程池 1.  线程概念 1.1  什么是线程 1.2  线程的好处 2.   创建线程的三种方式 注意事项 2.1  继承Thread类 2.1.1 认识  2.1.2  编码实现  package cn.hdc.oop10.Thread;import org.slf4j.Logger;import org.slf4j.LoggerFactory
阅读更多...
康拓展开（hash算法中会用到）

康拓展开（hash算法中会用到）

康拓展开是一个全排列到一个自然数的双射（也就是某个全排列与某个自然数一一对应） 公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。（a[i]在不同应用中的含义不同）； 典型应用： 计算当前排列在所有由小到大全排列中的顺序，也就是说求当前排列是第
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2