浅谈SSIM 损失函数计算

前言

最近研究图像重建老是看到SSIM损失函数，但是去找了那篇论文《Image Quality Assessment: From Error Visibility to Structural Similarity》挺有意思的。

Structural Similarity

作者把两幅图 x, y 的相似性按三个维度进行比较：亮度（luminance）l(x,y)，对比度（contrast）c(x,y)，和结构（structure）s(x,y)。最终 x 和 y 的相似度为这三者的函数：

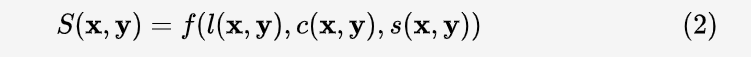
其中l（x,y）,c(x,y).s(x,y)三个公式定量计算这三者的相似性，公式的设计遵循三个原则：
1.对称性：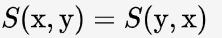
2.有界性 :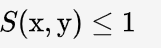
3.极值唯一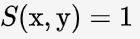, 当且仅当 x = y

亮度相似性

如果一幅图有 N 个像素点，每个像素点的像素值为 xi，那么该图像的平均亮度为：

则两幅图 x 和 y 的亮度相似度：

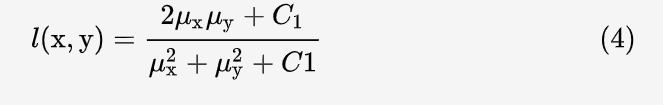
这里 C1是为了防止分母为零的情况，且：

其中 K1<<1是一个常数，具体代码中的取值为 0.01，L 是灰度的动态范围，由图像的数据类型决定，如果数据为 uint8 型，则 L=255。可以看出，公式 (4) 对称且始终小于等于1，当 x = y时为1。

对比度相似性

所谓对比度，就是图像明暗的变化剧烈程度，也就是像素值的标准差。其计算公式为：

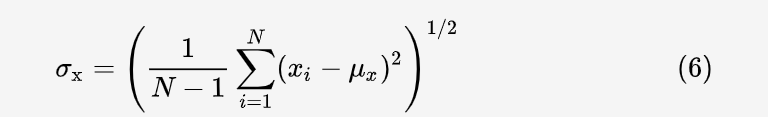
对比度的相似度公式和公式 (4) 极为相似，只不过把均值换成了方差，定义为：

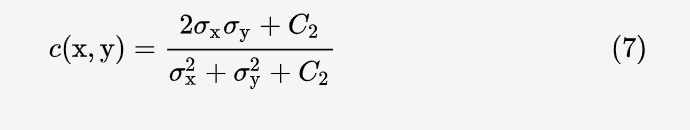
其中：

K2一般在代码中取 0.03。公式 (7) 也对称且小于等于1，当 x = y 时等号成立.

结构相似度

需要注意的是，对一幅图而言，其亮度和对比度都是标量，而其结构显然无法用一个标量表示，而是应该用该图所有像素组成的向量来表示。同时，研究结构相似度时，应该排除亮度和对比度的影响，即排除均值和标准差的影响。归根结底，作者研究的是归一化的两个向量：

之间的关系。根据均值与标准差的关系，可知这两个向量的模长均为 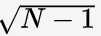因此它们的余弦相似度为：

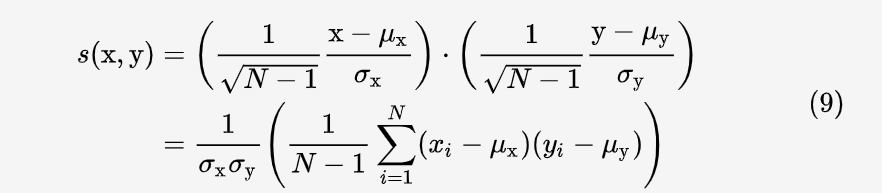
上式中第二行括号内的部分为协方差公式：

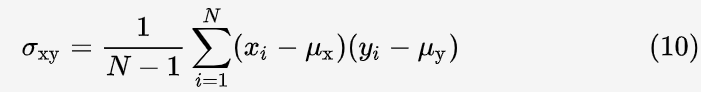
同样为了防止分母为0，分子分母同时加 C3.
最终s（x，y）

令 c3=c2/2 ， c(x,y)的分子和 s(x,y) 的分母可以约分，最终得到 SSIM 的公式：

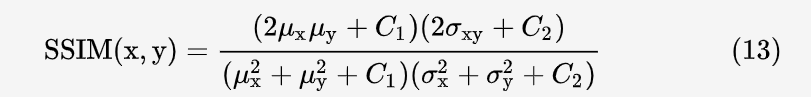
SSIM 实现

然而，上面的 SSIM 不能用于一整幅图。因为在整幅图的跨度上，均值和方差往往变化剧烈；同时，图像上不同区块的失真程度也有可能不同，不能一概而论；此外类比人眼睛每次只能聚焦于一处的特点。作者采用 sliding window （这里可以看做卷积）以步长为 1 计算两幅图各个对应 sliding window 下的 patch 的 SSIM，然后取平均值作为两幅图整体的 SSIM，称为 Mean SSIM。简写为 MSSIM（注意和后续出现的 multi-scale SSIM：MS-SSIM 作区分）。
如果像素 Xi对应的高斯核权重为 Wi。那么加权均值，方差，协方差的公式为：

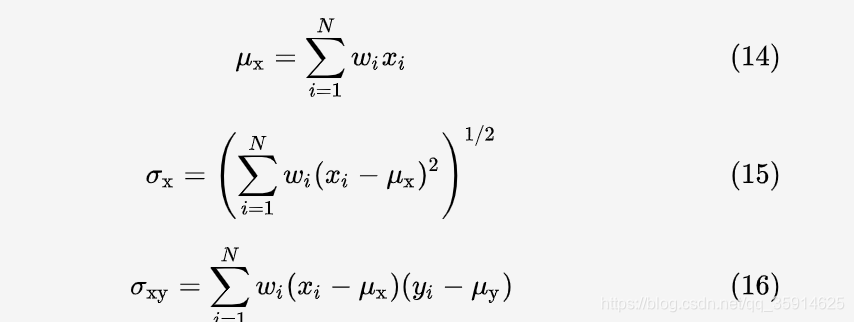
假如整幅图有 M 个 patch，那么 MSSIM 公式为：


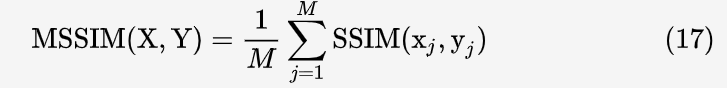
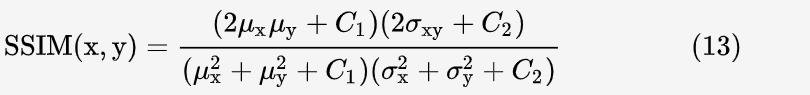
在我们用pytorch实现部分

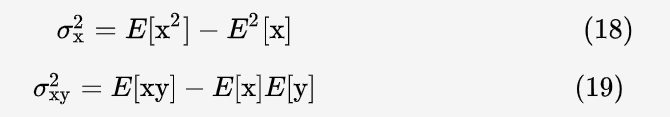
非加权平均包含在加权平均的情况之下，因此这里只推导加权的情况，若 wi 为权重，根据 (15)：

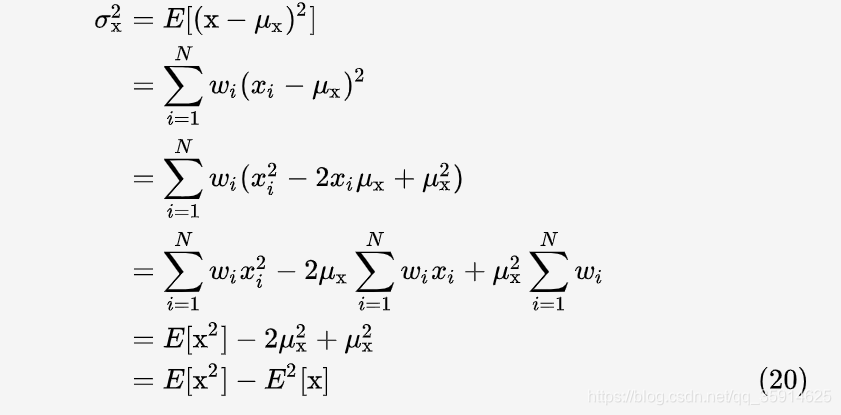
想求图像的方差，只需做两次卷积，一次是对原图卷积，一次是对原图的平方卷积，然后用后者减去前者的平方即可。

根据 (16)：

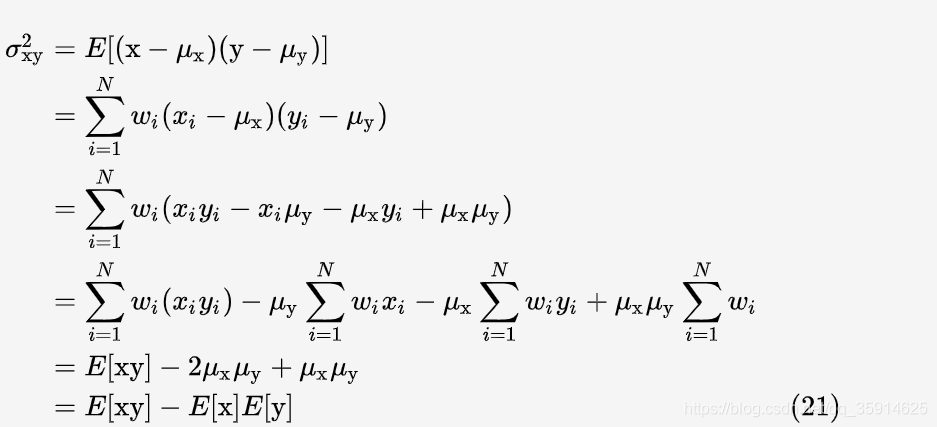
求两图的协方差，只需做三次卷积，第一次是对两图的乘积卷积，第二次和第三次分别对两图本身卷积，然后用第一次的卷积结果减去第二、三次卷积结果的乘积。

import torch
import torch.nn.functional as F
from torch.autograd import Variable
import numpy as np
from math import expdef gaussian(window_size, sigma):gauss = torch.Tensor([exp(-(x - window_size//2)**2/float(2*sigma**2)) for x in range(window_size)])return gauss/gauss.sum()def create_window(window_size, channel):_1D_window = gaussian(window_size, 1.5).unsqueeze(1)_2D_window = _1D_window.mm(_1D_window.t()).float().unsqueeze(0).unsqueeze(0)window = Variable(_2D_window.expand(channel, 1, window_size, window_size).contiguous())return windowdef _ssim(img1, img2, window, window_size, channel, size_average = True):mu1 = F.conv2d(img1, window, padding = window_size//2, groups = channel)mu2 = F.conv2d(img2, window, padding = window_size//2, groups = channel)mu1_sq = mu1.pow(2)mu2_sq = mu2.pow(2)mu1_mu2 = mu1*mu2sigma1_sq = F.conv2d(img1*img1, window, padding = window_size//2, groups = channel) - mu1_sqsigma2_sq = F.conv2d(img2*img2, window, padding = window_size//2, groups = channel) - mu2_sqsigma12 = F.conv2d(img1*img2, window, padding = window_size//2, groups = channel) - mu1_mu2C1 = 0.01**2C2 = 0.03**2ssim_map = ((2*mu1_mu2 + C1)*(2*sigma12 + C2))/((mu1_sq + mu2_sq + C1)*(sigma1_sq + sigma2_sq + C2))if size_average:return ssim_map.mean()else:return ssim_map.mean(1).mean(1).mean(1)class SSIM(torch.nn.Module):def __init__(self, window_size = 11, size_average = True):super(SSIM, self).__init__()self.window_size = window_sizeself.size_average = size_averageself.channel = 1self.window = create_window(window_size, self.channel)def forward(self, img1, img2):(_, channel, _, _) = img1.size()if channel == self.channel and self.window.data.type() == img1.data.type():window = self.windowelse:window = create_window(self.window_size, channel)if img1.is_cuda:window = window.cuda(img1.get_device())window = window.type_as(img1)self.window = windowself.channel = channelreturn _ssim(img1, img2, window, self.window_size, channel, self.size_average)def ssim(img1, img2, window_size = 11, size_average = True):(_, channel, _, _) = img1.size()window = create_window(window_size, channel)if img1.is_cuda:window = window.cuda(img1.get_device())window = window.type_as(img1)return _ssim(img1, img2, window, window_size, channel, size_average)

总结

下面的 GIF 对比了 MSE loss 和 SSIM 的优化效果，最左侧为原始图片，中间和右边两个图用随机噪声初始化，然后分别用 MSE loss 和 -SSIM 作为损失函数，通过反向传播以及梯度下降法，优化噪声，最终重建输入图像。：