运算放大器（二）：恒流源

2023-10-11 14:30
文章标签 运算 放大器 恒流源

本文主要是介绍运算放大器（二）：恒流源，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、实现原理

       恒流源的输出电流能够在一定范围内保持稳定，不会随负载的变化而变化。
       通过运放，将输入的电压信号转换成满足一定关系的电流信号，转换后的电流相当一个输出可调的简易恒流源。       

二、电路结构
  1. 常用的恒流源电路如下 图1 所示，由运放、MOS（三极管）、负载（R_{L}）、限流电阻（R_{S}）等组成；
    其输出电流为  I_{out}=\frac{V_{ref}}{R_{s}}

                                                                                         图1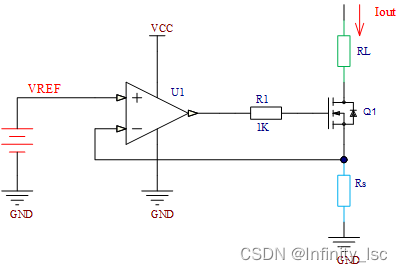
    假设参考电压为 3.3V，限流电阻 R_{S} = 1KΩ，即恒流源电流为 3.3mA，若负载电压为 5V，意味着电路最大带载能力 R_{L} = 1.52KΩ，超过该值，输出电流将不再稳定
  2. 另一种负载接地的电压-电流转换电路如 图2 所示，即模电课本教学的电路

                                                                                                 图2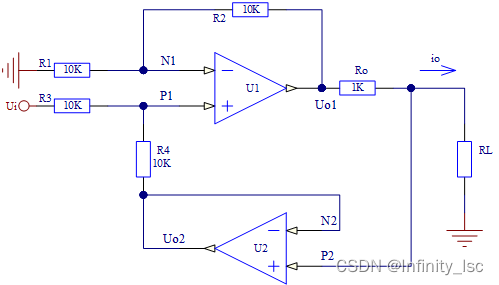
    U1构成同相求和电路，U2构成电压跟随器，根据虚短和虚断，可得：

    U_{O2}=U_{P2}

    U_{P1}=\frac{R_{4}}{R_{3}+R_{4}}\cdot U_{I}+\frac{R_{3}}{R_{3}+R_{4}}\cdot U_{​{P2}}=0.5U_{I}+0.5U_{P2}

    U_{O1}=\left ( 1+\frac{R_{2}}{R_{1}} \right )\cdot U_{P1}=2U_{P1}

    整理可得 U_{O1}=U_{P2}+U_{I}，R_{O}上的电压 U_{R_{O}}=U_{O1}-U_{P2}=U_{I}

    \therefore i_{O}=\frac{U_{I}}{R_{O}}
  3. 图2 中电路用MOS（三极管）改进后，可提高输出电流能力，如 图3 所示 

                                                                                                        图3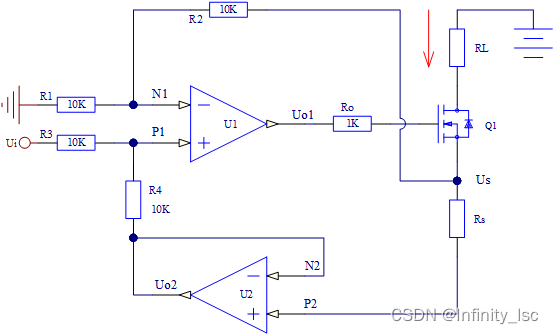
     \frac{U_{S}-U_{N1}}{R_{2}}=\frac{U_{N1}}{R_{1}}

    \therefore ^{U_{S}}=2U_{N1}=2U_{P1}

    i_{S}=\frac{U_{S}-U_{P2}}{R_{S}}=\frac{2U_{P1}-U_{P2}}{R_{S}}=\frac{U_{I}+U_{P2}-U_{P2}}{R_{S}}=\frac{U_{I}}{R_{S}}  

这篇关于运算放大器（二）：恒流源的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/188700。

相关文章

全屋WiFi 7无死角! 华硕 RP-BE58无线信号放大器体验测评

全屋WiFi 7无死角! 华硕 RP-BE58无线信号放大器体验测评

《全屋WiFi7无死角!华硕RP-BE58无线信号放大器体验测评》家里网络总是有很多死角没有网，我决定入手一台支持Mesh组网的WiFi7路由系统以彻底解决网络覆盖问题，最终选择了一款功能非常... 自2023年WiFi 7技术标准（IEEE 802.11be）正式落地以来，这项第七代无线网络技术就以超高速
阅读更多...
C/C++中OpenCV 矩阵运算的实现

C/C++中OpenCV 矩阵运算的实现

《C/C++中OpenCV矩阵运算的实现》本文主要介绍了C/C++中OpenCV矩阵运算的实现,包括基本算术运算（标量与矩阵）、矩阵乘法、转置、逆矩阵、行列式、迹、范数等操作,感兴趣的可以了解一下... 目录矩阵的创建与初始化创建矩阵访问矩阵元素基本的算术运算 ➕➖✖️➗矩阵与标量运算矩阵与矩阵运算 (逐元
阅读更多...
Python位移操作和位运算的实现示例

Python位移操作和位运算的实现示例

《Python位移操作和位运算的实现示例》本文主要介绍了Python位移操作和位运算的实现示例,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一... 目录1. 位移操作1.1 左移操作 (<<)1.2 右移操作 (>>)注意事项：2. 位运算2.1
阅读更多...
【Prometheus】PromQL向量匹配实现不同标签的向量数据进行运算

【Prometheus】PromQL向量匹配实现不同标签的向量数据进行运算

✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯，先赞后看哦~🎈🎈 🏆 作者简介：景天科技苑 🏆《头衔》：大厂架构师，华为云开发者社区专家博主，阿里云开发者社区专家博主，CSDN全栈领域优质创作者，掘金优秀博主，51CTO博客专家等。 🏆《博客》：Python全栈，前后端开发，小程序开发，人工智能，js逆向，App逆向，网络系统安全，数据分析，Django，fastapi
阅读更多...
uva 575 Skew Binary（位运算）

uva 575 Skew Binary（位运算）

求第一个以（2^(k+1)-1)为进制的数。 数据不大，可以直接搞。 代码： #include <stdio.h>#include <string.h>const int maxn = 100 + 5;int main(){char num[maxn];while (scanf("%s", num) == 1){if (num[0] == '0')break;int len =
阅读更多...
【Java中的位运算和逻辑运算详解及其区别】

【Java中的位运算和逻辑运算详解及其区别】

Java中的位运算和逻辑运算详解及其区别 在 Java 编程中，位运算和逻辑运算是常见的两种操作类型。位运算用于操作整数的二进制位，而逻辑运算则是处理布尔值 (boolean) 的运算。本文将详细讲解这两种运算及其主要区别，并给出相应示例。 应用场景了解 位运算和逻辑运算的设计初衷源自计算机底层硬件和逻辑运算的需求，它们分别针对不同的处理对象和场景。以下是它们设计的初始目的简介：
阅读更多...
位运算:带带孩子吧，孩子很强的！

位运算:带带孩子吧，孩子很强的！

快速进制 在聊到位运算之前，不妨先简单过一遍二进制的东西。熟悉二进制和十进制的快速转换确实是掌握位运算的基础，因为位运算直接在二进制位上进行操作。如果不熟悉二进制表示，很难直观理解位运算的效果。 这里主要涉及二进制和十进制之间的互相转换。 十进制转二进制 十进制转二进制可以使用常见的 除2取余法 进行。每次将十进制除以2并记录所得余数，直到商为0，然后再将记录的余数 从下往上排列即
阅读更多...
快速幂运算的一些模板

快速幂运算的一些模板

这里用递归和循环两种做法来做。 简单来说，快速幂就是把底数扩大，指数缩小，比如2*2=4；计算2的幂时，就可以转换成4的幂来运算，这样可以避免在计算大的数据时爆int的现象  //递归int power(int a,int n){int ans;if(n==2) ans=1;else{ans=power(a*a,n/2);if(n%2==1) ans*=a;}return ans;}
阅读更多...
高精度计算----减法运算(浮点型)

高精度计算----减法运算(浮点型)

基于上一贴，修改减法运算适合于高精度浮点型计算。 因为减法比加法难度大一点，考虑的地方也要多一些，可能代码有欠缺，欢迎指出。 运算说明： 1、相减函数依旧没改变，包括上一贴的判断被减数与减数的大小函数也没变。 2、增加两个函数，取小数位数函数和结果处理（回归小数点）函数 3、与加法浮点高精度运算相比，这里改变较多的是结果处理函数，加法加完后，位数不减反增，而且最多增一位。减法会消失掉好多
阅读更多...
高精度计算----减法运算

高精度计算----减法运算

处理大数减法运算： 1、首先要判断被减数与减数哪个更大，再相应的带入减法函数去处理。具体的比较可以使用字符串的相关知识去比较。 2、相减要先对齐数组，依照减数的长度，执行相应的减法运算次数。 3、不需要借位相减的话，直接减去；需要的话，向前借一位，若前一位是0，则再前借（此时前一位的0变为10）。 测试程序效果如下：   以下代码包括相减函数，比较被减数减数函数，若有错误，请指出：
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2