运算符之位运算符 [详解]

运算符可分下列运算符,本篇只研究位运算符

注1:逻辑运算符和位运算符因为存在部分符号相同,所以上面划线表示需要注意区分两者 

注2:需要掌握前置知识,指的是需要知道进制如何转换,具体是要知道二进制和十进制怎么互换。不清楚的可以看[这里]

1、位运算符

位运算(bitwise operators)定义

        现代计算机中所有的数据都以二进制的形式存储在设备中,即 0、1 两种状态。计算机对二进制数据进行的运算(+、-、*、/)都是叫位运算,注意符号位也共同参与运算

二进制数据指的是整数类型的位,整数类型包括byte,short,int,long,char

对二进制数据的运算严格讲是对二进制的位进行运算,即按位运算,按位运算就用到了位运算符。按位运算表示按每个二进制位（bit）进行计算,其操作数和运算结果都是整型值

注1:位运算符的操作数只能是整型或者字符型数据以及它们的变体,不用于 float、double 或者 long 等复杂的数据类型->究竟包不包含long类型呢?不清楚

位运算示例:计算两个数的和

int a = 35;
int b = 47;
int c = a + b;

在计算机中都是以二进制来进行运算,所以上面 int 变量会在机器内部先转换为二进制再进行相加

35:  0 0 1 0 0 0 1 1
47:  0 0 1 0 1 1 1 1
————————————————————
82:  0 1 0 1 0 0 1 0

相比代码中直接使用(+、-、*、/)运算符,合理的运用位运算更能显著提高代码在机器上的执行效率

2、位运算符组成

一开始的七个位运算符可以再分为位逻辑运算符和位移运算符。前四个是位逻辑运算符,后三个是位移运算符(也可以叫移位运算符) 

注1:除了 ~（取反）为单目运算符外,其余都为双目运算符。双目指的是有两个数据参与运算

2.1、按位与(&)

定义:参加运算的两个数据,按二进制位进行"与"运算

注1:定义中的"数据"是指的"二进制下的数据"。如果是十进制的数据则还需要转为二进制才能作为位运算的操作数据。所以知道进制间如何转换是必须要掌握的,这点再次强调

注2:不光是按位与,其他位运算符的操作数据也都是二进制形式的

运算规则

0&0=0  0&1=0  1&0=0  1&1=1

总结:两位同时为1时,结果才为1,否则结果为0->可以简记为"同一才一"

例如    3&5     即0000 0011
& 0000 0101 
= 0000 0001因此 3&5 的值是1

规则补充:参与运算的数字,低位对齐,高位不足的补零->不同长度的数据进行位运算:如果两个不同长度的数据进行位运算时，系统会将二者按右端对齐，然后进行位运算。不同长度是因为"位运算针对的是整数类型的数据,整数类型包括byte、short、int、long、char这个多类型",如int类型的字面量12和byte类型的字面量55进行运算,位数就需要补齐补全后才可以进行按位运算。

注意:负数按补码形式参加按位与运算->依据是"参与运算的数据都是二进制的补码形式",那么前面"操作数据都是二进制形式"完整表述是"操作数据都是二进制补码形式"。依据这点又应该是参照"二进制底层都是补码形式"和"字面量转为二进制进行运算,都是转的二进制的补码形式"得出的

与运算的用途

1）清零

如果想将一个单元清零,即使其全部二进制位为0。只要与一个各位都为零的数值相与,结果为零->即任何数与 0 进行按位与运算,其结果都为 0

2）取一个数的指定位

        比如取数 X=1010 1110 的低4位,只需要另找一个数Y,令Y的低4位为1,其余位为0。即Y=0000 1111,然后将X与Y进行按位与运算（X&Y=0000 1110）即可得到X的指定位->清零是与全部位为0的二进制进行与运算;而取特定位是取一个二进制数值,对应指定位的几位取1

3）判断奇偶

只要根据最未位是0还是1来决定,为0就是偶数、为1就是奇数。因此可以用if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是不是偶数

2.2、按位或（|）

定义:参加运算的两个对象,按二进制位进行"或"运算

运算规则

0|0=0  0|1=1  1|0=1  1|1=1

总结:参加运算的两个对象只要有一个为1,其值为1->简记"有一则一"

例如    3|5    即 0000 0011
| 0000 0101 
= 0000 0111因此,3|5的值得7

规则补充:参与运算的数字,低位对齐,高位不足的补零 

注意:负数按补码形式参加按位或运算

或运算的用途

常用来对一个数据的某些位设置为1

比如将数 X=1010 1110 的低4位设置为1,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位或运算（X|Y=1010 1111）即可得到

2.3、按位异或（^）

定义:参加运算的两个数据,按二进制位进行"异或"运算

运算规则

0^0=0  0^1=1  1^0=1  1^1=0

总结:参加运算的两个对象,如果两个相应位相同为0,相异为1->简记"同为零、异为一"

规则补充:参与运算的数字，低位对齐，高位不足的补零 

异或的几条性质

• 1、交换律
• 2、结合律 (a^b)^c == a^(b^c)
• 3、对于任何数x，都有 x^x=0，x^0=x
• 4、自反性: a^b^b=a^0=a;

下面详细说说

Ⅰ、异或运算符满足交换律

也就是说 , a^b与b^a是等价的，虽然a和b交换了位置，但还是会运算出相同的结果。这个规律还可以推广到N个操作数，也就是说，如果有N个变量都参与了异或运算，那么它们的位置无论如何交换，运算的结果都是相同的

Ⅱ、任何两个相同的数字进行异或操作，所得到的结果都必然为0

这个特性并不难理解，因为两个相同的数字，换算成补码后，每个二进制位上的数也都相同，这样在进行异或运算时，按照运算规则，每个二进制位上得到的运算结果也都是0，这N个0所组成的二进制串就是数字0的补码。我们可以利用这个特性快速的判断两个整数是否相同。另外,利用这个特性还可以实现内存的快速清零操作，比如我们可以在代码中写上a=a^a;这条语句能快速的把变量a所占据的那几个字节的内存迅速清零

Ⅲ、对于任意一个二进制位来说，这个位上的数与0进行异或运算，运算结果与这个二进制位上的数是相同的，而与1进行异或运算，结果与这个二进制位上的数字相反

注意，我们现在说的是二进制位上的数字，所谓相反不是说原来这个位上是1，运算结果是-1，而是说原来是1，运算结果为0，原来如果是0，运算结果是1，这才是此处所说的”相反”的概念。在以后进行一些位运算操作的时候经常会用到这个特性

Ⅳ、对于任何两个整数a和b，a^b^b等于a

这个结论为什么成立呢？简单说来，就是因为这个表达式中有b^b，而b^b的结果为0，前文已讲过，任何一个数与0进行按位异或操作，结果仍然是这个数本身，所以，a^b^b等于a。这个特性在加密运算方面有着很普遍的应用。我们可以把a当作要加密的数据，而把b当作密钥。a异或b就是把a用密钥b进行了加密操作，当需要解密时，仍然以b作为密钥，再进行一次异或就实现了解密。

这个特性还可以推出另外一个结论:对于任何两个整数a和b , a^b^a等于b。我们能够得到这个结论的原因也很简单,就是因为按照交换律，a^b与b^a的运算结果是一样的，所以a^b^a等价于b^a^a，这个表达式中出现了a^a，a^a的值也为0，所以整个表达式的其实就相当于b^0，最终结果还是b

提示:在有的高级语言中,将运算符^作为求幂运算符,要注意区分

异或运算的用途

1）翻转指定位

比如将数 X=1010 1110 的低4位进行翻转，只需要另找一个数Y，令Y的低4位为1，其余位为0，即Y=0000 1111，然后将X与Y进行异或运算（X^Y=1010 0001）即可得到。

2）与0相异或值不变

例如：1010 1110 ^ 0000 0000 = 1010 1110

3）交换两个数

void Swap(int &a, int &b){if (a != b){a ^= b;b ^= a;a ^= b;}
}

2.4、按位取反 (~)

定义:参加运算的一个数据，按二进制进行"取反"运算

运算规则

~1=0
~0=1

总结:对一个二进制数按位取反,即将0变1、1变0->简记"取反:0变1、1变0"

~(取反)使用示例: ~4表示对4取反,得到结果-5 

运算过程有必要讲讲。按理说对4取反是:0100取反是1011,转为十进制就是-3,为什么是-5呢?

~4
求出十进制4的二进制形式:0100
但是针对的是byte、shhort、int、long、char这些(一般方便省事就用一个字节表示了,这点容易出错)
所以4的二进制应为    省略三个字节的0,再跟0000 0100
再取反(省略三个字节的0,再跟0000 0100 用一个字节的0000 0100演示转换过程一样所以用后者演示)
0000 0100
1111 1011
二进制转十进制需要先转反再转原,这才能转十进制
所以
1111 1011
1111 1010
1000 0101得到十进制结果-5

注意取反是符号位也取反,但是二进制转十进制则需要补转反转原才能转十 

取反运算的用途

使一个数的最低位为零

使a的最低位为0，可以表示为：a & ~1。~1的值为 1111 1111 1111 1110，再按"与"运算，最低位一定为0。因为" ~"运算符的优先级比算术运算符、关系运算符、逻辑运算符和其他运算符都高

如果是对变量进行取反操作，那么经过操作之后，变量的值并不会发生变化

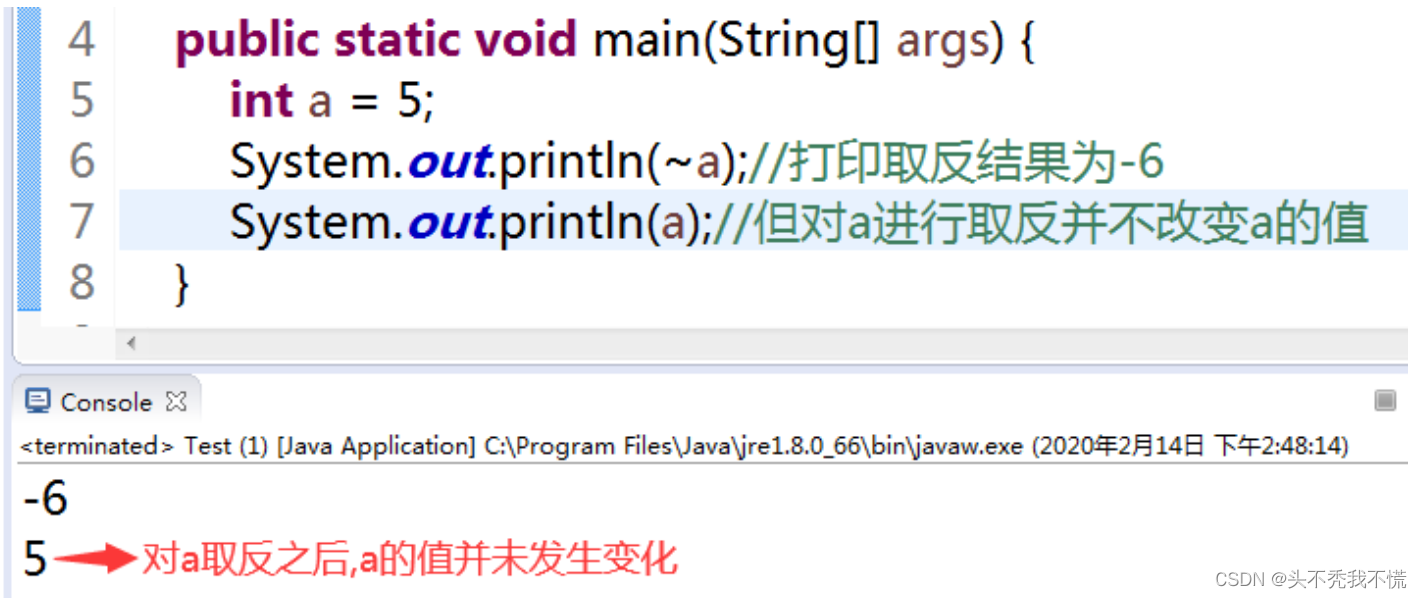
说明变量a经过取反得到的那个-6并没有被赋值到变量a上。通过这个例子可以证明:取反运算并没有对变量重新赋值的功能。取反运算的结果只是临时保存在操作数栈中,变量本身的值不会因取反操作而发生改变 

下面讲位移运算符

        位移运算符用来将操作数向某个方向（向左或者右）移动指定的二进制位数

2.5、无符号左移（<<）

定义:将一个运算对象的各二进制位全部左移若干位。左边的二进制位丢弃,右边的补0

设 a=1010 1110 , a = a<< 2 就是将a的二进制位整体左移2位,左移的两位会丢弃,右补缺的两位会补上0,即得a=1011 1000

若左移时舍弃的高位不包含1,则每左移一位相当于该数乘以2->这句话再想想

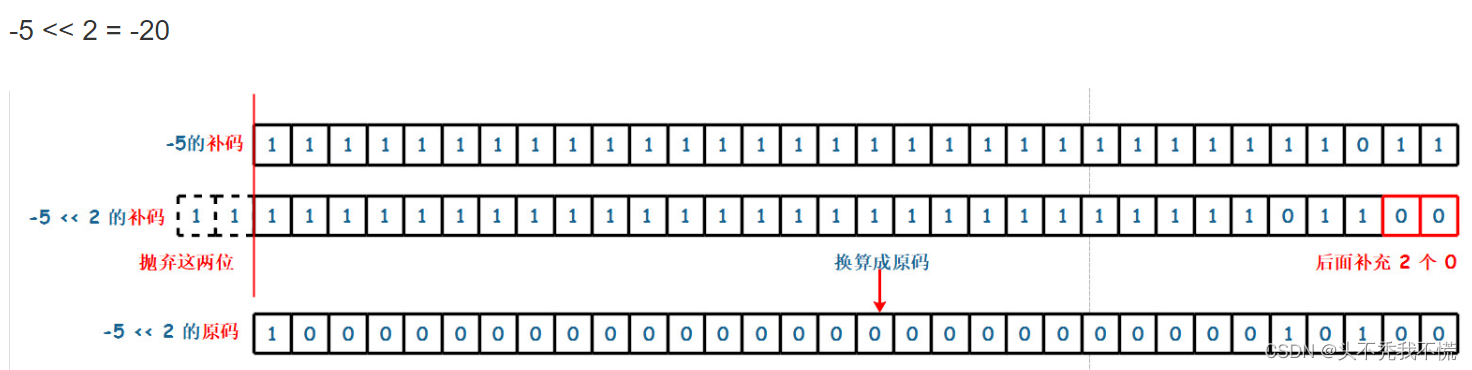
"左边丢弃位,右边补零"就是如上图第二行的意思

左移运算有乘以2的N次方的效果

一个数向左移动1位就相当于乘以2的1次方,移动两位就相当于乘以2的2次方,也就是乘以4。位移操作在实际运算时远远快于乘法操作,所以在某些对运算速度要求非常高的场合可以考虑用左移代替乘以2的N次方的乘法操作。但是需要提醒大家注意三个细节

1、位移操作同取反操作一样,并不能改变变量本身的值,所能改变的仅是存储在操作数栈中那个数据的值。不理解的看下图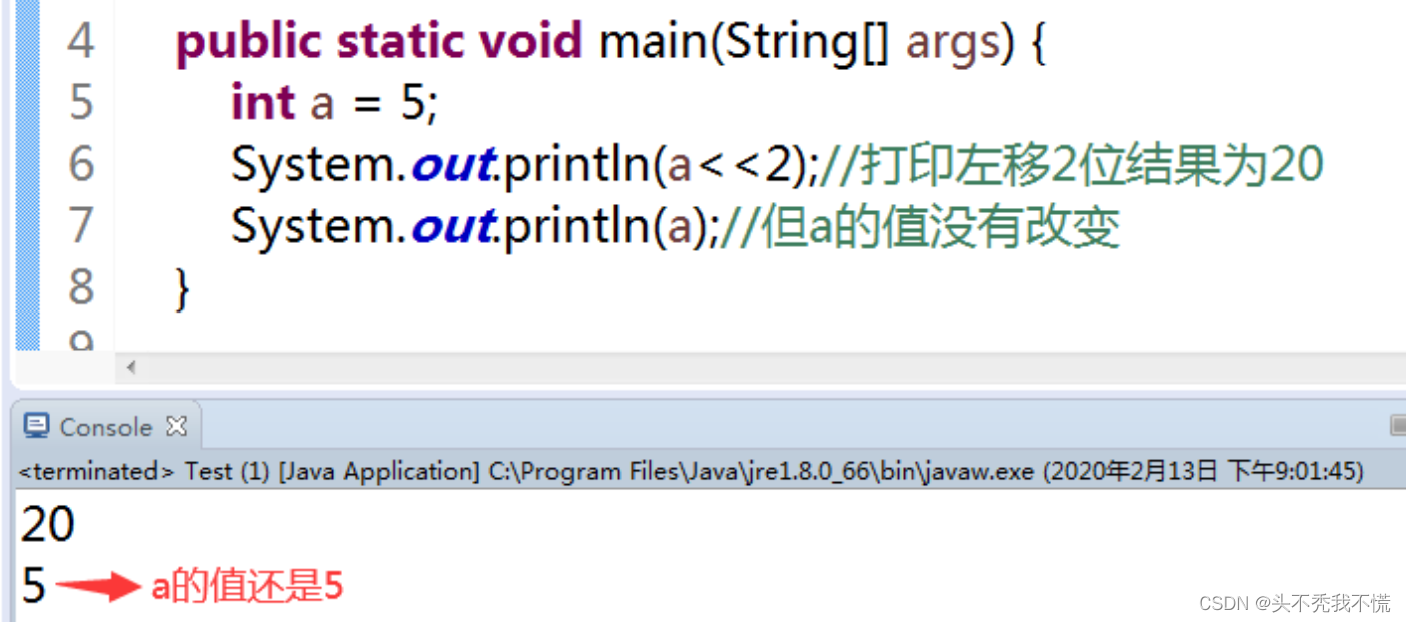

2、当位移的位数很多时会导致最左边的符号位发生变化,就不再具有乘以2的N次方的效果了

        比如十进制的5转换为补码形式是 : 3字节的0,再跟上0000 0101。如果移动29位,那么101前面24+4+1=29个零都丢弃了,此时高位是1。这时运算的结果就成为了一个负数,不再是5乘以2的29次方的乘法结果

3、对于byte/short/int三种类型的数据,Java语言最多支持31位的位移运算、对于long类型的数据而言,最多支持63位的位移运算。这可能是因为Java语言的设计者认为位移的偏移量已经超过存储数据本身的长度没有什么意义->其实2、3情况太特殊,一般不会这么夸张移动这么多位,了解就行了

2.6、带符号右移（>>）

定义：将一个数的各二进制位全部右移若干位,右边丢弃,是正数左边补0,是负数左边补1

操作数每右移一位,相当于该数除以2

注1:<<是无符号左移,那>>可能是无符号右移了。实际不是

注2:>>是带符号右移所以要考虑左边补0还是其他了,前面已说:正数左补0、负数左补1

带符号右移效果如下图

之前强调过"左移N位的操作具有乘以2的N次方的效果",其实带符号右移也具有”类似”除以2的N次方的效果。但是请注意,这里说的是“类似”除以2的N次方的效果

为什么要加上“类似”两个字呢？

就是因为对于正数而言,带符号右移之后产生的数字确实等于除以2的N次方。比如说我们把N的值设为3,对于正15,带符号右移3位的结果是1。这个结果与“15除以2的3次方”的结果是相同的

但是对于负数而言,带符号右移的效果分为两种情况

        如果这个负数是“2的N次方”的整数倍,那么带符号右移N位的效果也等于除以2的N次方。举例:N的值还是设为3,如果对于“-16”来说，它是“2的3次方”的整数倍，那么带符号右移3位的结果是-2，这个结果相当于“-16除以2的3次方”

        而如果这个负数不是“2的N次方”的整数倍。那么右移N位之后是在除以2的N次方的结果之上还要减去1。比如-15,它不是“2的3次方”的整数倍，那么带符号右移3位的结果是-2，这个运算结果其实就是“-15被2的3次方整除再减去1”。小伙伴们也可以用其他负整数来验证一下这个结论。因为并非每个负整数带符号右移的结果都等于除以“2的N次方”，我们才在文中添加了“类似”这两个字。

        带符号右移的操作可以保证移动之前和移动之后数字的正负属性不变，原来是正数，不管移动多少位，移动之后还是正数 ; 原来是负数，移动之后还是负数

另外,我们还可以继续深挖一下这个特性从而得到一个结论:对于任何一个byte、short或者int类型的数据而言,带符号右移31位(或更多位)之后得到的必然是0或者是-1。对于long类型的数据而言,带符号右移63位(或更多位)之后得到的也必然是0或者是-1。能够得出这个结论的依据也很简单，就是因为对于byte、short和int类型的变量而言，如果是正数，带符号右移31位之后产生的二进制串必然全部是0，转换成对应的十进制数就是0；而对于负数而言，带符号右移31位之后产生的二进制串必然全部是1，转换成十进制数就是-1。对于long类型的数据，带符号右移63位也具有相同效果

2.7、无符号右移运算符

右移运算分为两种,分别是带符号右移和无符号右移。现在再来讲解无符号右移

无符号右移运算符的写法是”>>>”,比带符号右移多了一个”>”。带符号右移的运算规则与无符号右移的运算规则差别就在于:无符号右移在二进制串移动之后,空位由0来补充,与符号位是0还是1毫无关系。如下图

 

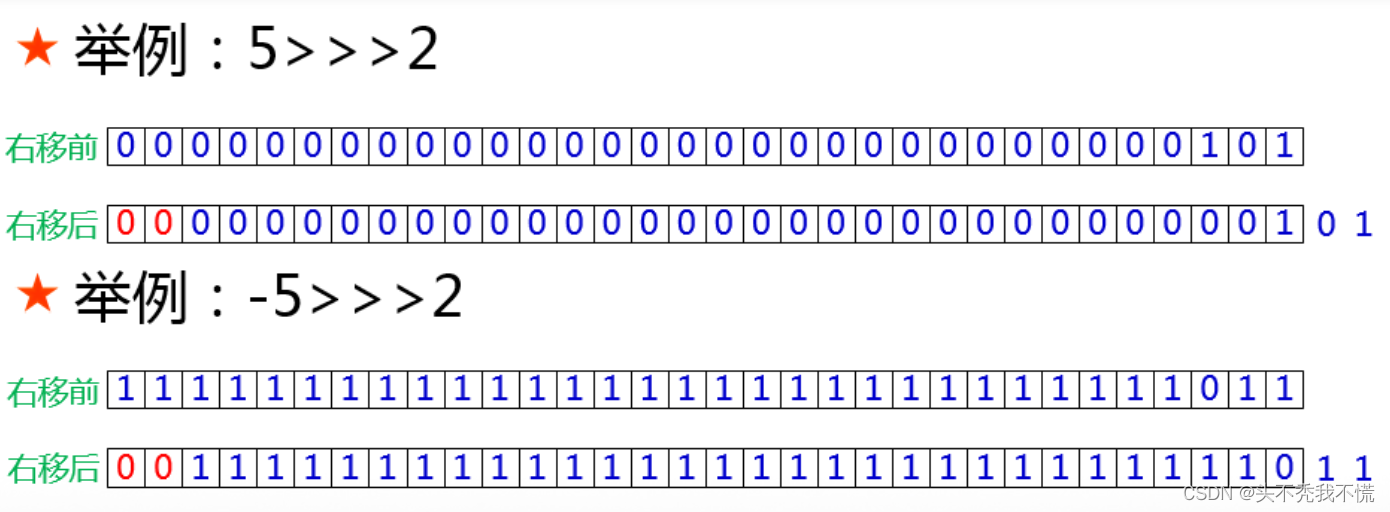
对于正数而言,无符号右移和带符号右移没有什么区别。而对于负数而言,经过无符号右移会产生一个正数,因为最左边的符号位被0填充了 

举例

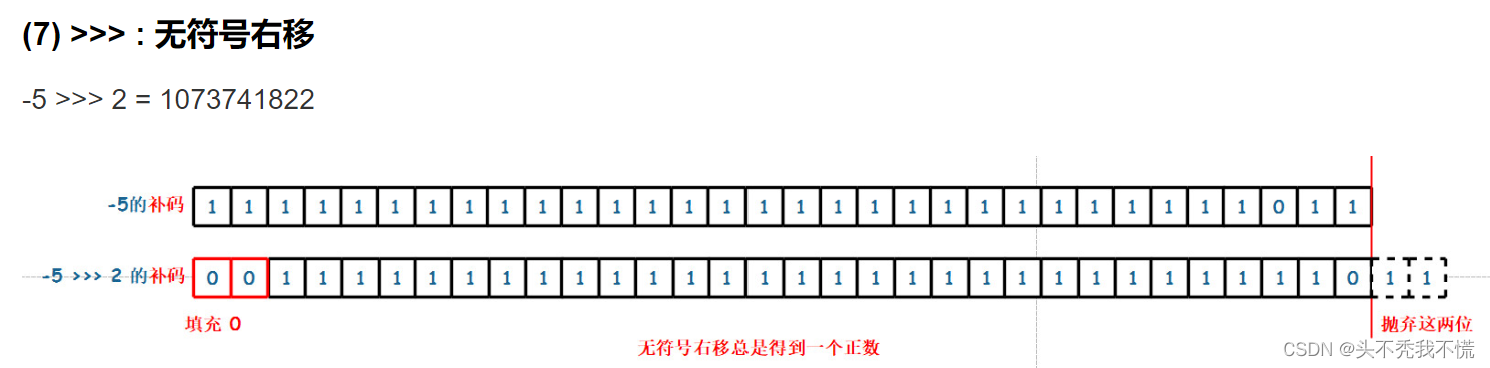
-6>>>3,结果是5 3687 0911

2.8、最终可以归纳为下表

位运算符	位运算符描述	功能	功能简记
&	按位与(AND)	两个位都为1时,结果才为1	同一才一
|	按位或(OR)	两个位都为0时，结果才为0	有一则一
^	按位异或(XOR)	两个位相同为0，相异为1	同为零异为一
~	按位取反(NOT)	0变1，1变0	取反,1变0,0变1
<<	无符号左移	各二进位全部左移若干位，高位丢弃，低位补0	二进制位全部左移n位,高位舍弃,低位补零
>>	带符号右移	各二进位全部右移若干位,低位移出（舍弃），正数高位补0、负数高位补1
>>>	无符号右移	各二进位全部右移若干位,低位移出（舍弃）,高位不分正负补0就完事了

掌握这七个位运算符后,我们还可以再看

2.9、复合赋值运算符

所有的二进制位运算符都有一种将赋值与位运算符组合在一起的简写形式。复合位赋值运算符由赋值运算符与位逻辑运算符和位移运算符组合而成。下面列出复合位赋值运算符的各种组合

运算符	含义	实例	结果
&=	按位与赋值	num1 &= num2	等价于 num 1=num 1 & num2
|=	按位或赋值	num1 |= num2	等价于 num 1=num 1 | num2
^=	按位异或赋值	num1 ^= num2	等价于 num 1=num 1 ^ num2
-=	按位取反赋值	num1 -= num2	等价于 num 1=num 1 - num2
«=	按位左移赋值	num1 «= num2	等价于 num 1=num 1 « num2
»=	按位右移赋值	num1 »= num2	等价于 num 1=num 1 » num2

看例子:下面定义了几个 int 型变量,然后运用位赋值简写的形式将运算后的值赋给相应的变量

package com.test.bit;public class BitTest {测试复合位赋值运算符public static void me1() {int a = 1;int b = 2;int c = 3;a &= 4;System.out.println(a);a |= 4;System.out.println(a);a ^= c;System.out.println(a);a -= 6;b >>= 1;c <<= 1;System.out.println("a = " + a);System.out.println("b = " + b);System.out.println("c = " + c);}public static void main(String[] args) {me1();}}结果是
0
4
7
a = 1
b = 1
c = 6

3、拓展

看两个例子,不难,就是输出没见过这里了解一下

int i = 10;
System.out.printf("%d \n",~i);

输出结果:十进制下的-11

int i=10;
System.out.printf("%x \n",~i);

输出结果:十六进制下的fff5 

Java面试题：请解释“&”和“&&”的区别？

1、对于“&&”主要应用在逻辑运算中，表示短路与操作，在进行若干个条件判断的时候，如果有条件返回了false，那么后续的条件都不判断，最终的判断的结果就是false；

2、对于“&”有两种使用环境

A、逻辑运算：表示所有的判断条件都会执行，不管是否遇见有返回false的判断条件；

B、位运算：表示进行位与的计算，如果两位的内容都是1结果才是1，如果有一位是0，那么位与的结果就是0

Java面试题：请解释“|”和“||”的区别？

1、对于“||”主要在逻辑运算上使用，表示短路或操作，在进行多个条件判断的时候，如果存在有true，后续的条件不再判断，最终的结果就是true

2、对于“|”有两种使用环境：

A、逻辑运算：表示所有的判断条件都会执行，不管是否遇见有返回true的判断条件；

B、位运算：表示进行位或的计算，如果两位有一位1结果就是1，两位全部为0，结果才为0

关于"低位对齐,长度补全后才能运算",下面再补充

以"与运算"为例说明如下：我们知道在C语言中long型占4个字节，int型占2个字节，如果一个long型数据与一个int型数据进行"与运算"，右端对齐后，左边不足的位依下面三种情况补足，

• 1）如果整型数据为正数，左边补16个0
• 2）如果整型数据为负数，左边补16个1
• 3）如果整形数据为无符号数，左边也补16个0
• 如：long a=123；int b=1；计算a& b

注意

• 对于低于 int 类型(如byte、short和char)的操作数总是先自动转换为int类型后再移位
• 对于 int 类型的整数移位 a >> b, 当 b>32 时，系统先用 b 对 32 求余(因为 int 是 32 位)，得到的结果才是真正移位的位数，例如，a >> 33 和 a >> 1 的结果相同，而 a >> 32 = a
• 对于 long 类型的整数移位 a >> b, 当 b>64 时，系统先用 b 对 64 求余(因为 long 是 64 位)，得到的结果才是真正移位的位数
• 当进行移位运算时，只要被移位的二进制码没有发生有效位的数字丢失(对于正数而言，通常指被移出去的位全部是 0)，不难发现左移 n 位就相当于乘以 2 的 n 次方，右移 n 位则是除以 2 的 n 次方
• 进行移位运算不会改变操作数本身，只是得到了一个新的运算结果

在对操作数进行位移运算时候,系统会对位移大小进行优化。例如:对一个32位的 int 类型移动34位,如果位移数大于当前类型表示的最大位数，那么系统会34%32 = 2, 位移数是求余的结果，即 4 >> 2 和4 >> 34结果是一样的

0的反码，补码都是0->正数原反补一致

Java没有无符合数。换而言之,Java中的数都是有符号的