【 二叉树前中后序遍历】

本文主要是介绍【 二叉树前中后序遍历】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、二叉树的遍历方法

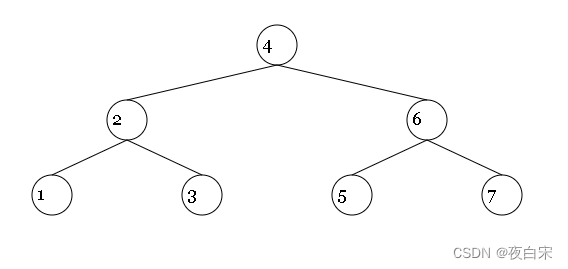
1. 广度优先遍历，又称层次遍历，
2. 深度优先遍历；
3. 其实所谓的前中后序遍历，都属于深度优先遍历，只是前中后序遍历的根节点输出顺序不一样，但是深度优先遍历的入栈顺序是一致的；
4. 前序遍历，即 根节点 左节点 右节点，遇到根节点就输出；
5. 中序遍历，即 左节点 根节点 右节点，左节点遍历完毕后输出根节点；
6. 后序遍历，即 左节点 右节点 根节点，右节点遍历完毕后输出根节点；
7. 如上图所示，其实每个节点对于当前树来说都是根节点，只是对于它的上级节点来说，有左右节点区分的概念；

二、前中后序遍历叙述

对于所有的深度遍历来说，都是从根节点出发，左子树遍历完毕后，再遍历右子树；

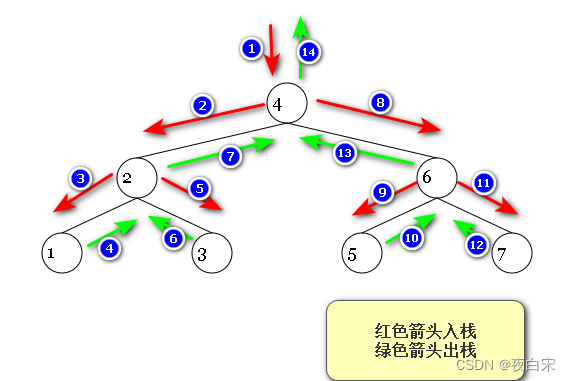
2.1 出入栈顺序

1. 从根节点出发，即节点4入栈；栈数据[4]
2. 访问节点4左子树，即节点2，也可以称为当前左子树的根节点，节点2入栈；栈数据[2,4]
3. 访问节点2左子树，即节点1，节点1入栈；栈数据[1,2,4]
4. 访问节点1左子树，节点1左子树为null，则节点1左子树访问完毕，然后访问节点1右子树，节点1右子树为null，则节点1右子树访问完毕，左右树全部访问完毕，则节点1出栈；栈数据[2,4];
5. 此时节点2的左子树访问完毕，访问节点2的右子树，节点2右子树为节点3，即节点3入栈；栈数据[3,2,4];
6. 访问节点3左子树，节点3左子树为null，则节点3左子树访问完毕，然后访问节点3右子树，节点3右子树为null，则节点3右子树访问完毕，左右树全部访问完毕，则节点3出栈；栈数据[2,4];
7. 此时节点2的右子树访问完毕，左右树全部访问完毕，则节点2出栈；栈数据[4];
8. 此时节点4的左子树访问完毕，访问节点4的右子树，节点4右子树为节点6，即节点6入栈；栈数据[6,4];
9. 访问节点6左子树，即节点5，节点5入栈；栈数据[5,6,4];
10. 访问节点5左子树，节点5左子树为null，则节点5左子树访问完毕，然后访问节点5右子树，节点5右子树为null，则节点5右子树访问完毕，左右树全部访问完毕，则节点5出栈；栈数据[6,4];
11. 此时节点6的左子树访问完毕，访问节点6的右子树，节点6右子树为节点7，即节点7入栈；栈数据[7,6,4];
12. 访问节点7左子树，节点7左子树为null，则节点7左子树访问完毕，然后访问节点7右子树，节点7右子树为null，则节点7右子树访问完毕，左右树全部访问完毕，则节点7出栈；栈数据[6,4];
13. 此时节点6的右子树访问完毕，左右树全部访问完毕，则节点6出栈；栈数据[4];
14. 此时节点4的右子树访问完毕，左右树全部访问完毕，则节点4出栈；栈数据[];
    

2.2 前序遍历（根节点优先输出）

1. 从根节点出发，即节点4入栈；输出节点4
2. 访问节点4左子树，即节点2，也可以称为当前左子树的根节点，节点2入栈；输出节点2
3. 访问节点2左子树，即节点1，节点1入栈；输出节点1
4. 访问节点1左子树，节点1左子树为null，则节点1左子树访问完毕，然后访问节点1右子树，节点1右子树为null，则节点1右子树访问完毕，左右树全部访问完毕，则节点1出栈；
5. 此时节点2的左子树访问完毕，访问节点2的右子树，节点2右子树为节点3，即节点3入栈；输出节点3
6. 访问节点3左子树，节点3左子树为null，则节点3左子树访问完毕，然后访问节点3右子树，节点3右子树为null，则节点3右子树访问完毕，左右树全部访问完毕，则节点3出栈；
7. 此时节点2的右子树访问完毕，左右树全部访问完毕，则节点2出栈；
8. 此时节点4的左子树访问完毕，访问节点4的右子树，节点4右子树为节点6，即节点6入栈；输出节点6
9. 访问节点6左子树，即节点5，节点5入栈；输出节点5
10. 访问节点5左子树，节点5左子树为null，则节点5左子树访问完毕，然后访问节点5右子树，节点5右子树为null，则节点5右子树访问完毕，左右树全部访问完毕，则节点5出栈；
11. 此时节点6的左子树访问完毕，访问节点6的右子树，节点6右子树为节点7，即节点7入栈；输出节点7
12. 访问节点7左子树，节点7左子树为null，则节点7左子树访问完毕，然后访问节点7右子树，节点7右子树为null，则节点7右子树访问完毕，左右树全部访问完毕，则节点7出栈；
13. 此时节点6的右子树访问完毕，左右树全部访问完毕，则节点6出栈；
14. 此时节点4的右子树访问完毕，左右树全部访问完毕，则节点4出栈；
15. 对应输出顺序为4->2->1->3->6->5->7

2.3 中序遍历（左节点全部遍历完毕，输出根节点）

1. 从根节点出发，即节点4入栈；
2. 访问节点4左子树，即节点2，也可以称为当前左子树的根节点，节点2入栈；
3. 访问节点2左子树，即节点1，节点1入栈；
4. 访问节点1左子树，节点1左子树为null，则节点1左子树访问完毕，输出节点1，然后访问节点1右子树，节点1右子树为null，则节点1右子树访问完毕，左右树全部访问完毕，则节点1出栈；
5. 此时节点2的左子树访问完毕，输出节点2，访问节点2的右子树，节点2右子树为节点3，即节点3入栈；
6. 访问节点3左子树，节点3左子树为null，则节点3左子树访问完毕，输出节点3，然后访问节点3右子树，节点3右子树为null，则节点3右子树访问完毕，左右树全部访问完毕，则节点3出栈；
7. 此时节点2的右子树访问完毕，左右树全部访问完毕，则节点2出栈；
8. 此时节点4的左子树访问完毕，输出节点4，访问节点4的右子树，节点4右子树为节点6，即节点6入栈；
9. 访问节点6左子树，即节点5，节点5入栈；
10. 访问节点5左子树，节点5左子树为null，则节点5左子树访问完毕，输出节点5，然后访问节点5右子树，节点5右子树为null，则节点5右子树访问完毕，左右树全部访问完毕，则节点5出栈；
11. 此时节点6的左子树访问完毕，输出节点6，访问节点6的右子树，节点6右子树为节点7，即节点7入栈；
12. 访问节点7左子树，节点7左子树为null，则节点7左子树访问完毕，输出节点7，然后访问节点7右子树，节点7右子树为null，则节点7右子树访问完毕，左右树全部访问完毕，则节点7出栈；
13. 此时节点6的右子树访问完毕，左右树全部访问完毕，则节点6出栈；
14. 此时节点4的右子树访问完毕，左右树全部访问完毕，则节点4出栈；
15. 对应输出顺序为1->2->3->4->5->6->7；
16. 如果是二叉搜索树，一般中序遍历就是用来排序输出的；

2.4 后序遍历（左右节点全部遍历完毕，输出根节点）

1. 从根节点出发，即节点4入栈；
2. 访问节点4左子树，即节点2，也可以称为当前左子树的根节点，节点2入栈；
3. 访问节点2左子树，即节点1，节点1入栈；
4. 访问节点1左子树，节点1左子树为null，则节点1左子树访问完毕，然后访问节点1右子树，节点1右子树为null，则节点1右子树访问完毕，左右树全部访问完毕，则节点1出栈；输出节点1
5. 此时节点2的左子树访问完毕，访问节点2的右子树，节点2右子树为节点3，即节点3入栈；
6. 访问节点3左子树，节点3左子树为null，则节点3左子树访问完毕，然后访问节点3右子树，节点3右子树为null，则节点3右子树访问完毕，左右树全部访问完毕，则节点3出栈；输出节点3
7. 此时节点2的右子树访问完毕，左右树全部访问完毕，则节点2出栈；输出节点2
8. 此时节点4的左子树访问完毕，访问节点4的右子树，节点4右子树为节点6，即节点6入栈；
9. 访问节点6左子树，即节点5，节点5入栈；
10. 访问节点5左子树，节点5左子树为null，则节点5左子树访问完毕，然后访问节点5右子树，节点5右子树为null，则节点5右子树访问完毕，左右树全部访问完毕，则节点5出栈；输出节点5
11. 此时节点6的左子树访问完毕，访问节点6的右子树，节点6右子树为节点7，即节点7入栈；
12. 访问节点7左子树，节点7左子树为null，则节点7左子树访问完毕，然后访问节点7右子树，节点7右子树为null，则节点7右子树访问完毕，左右树全部访问完毕，则节点7出栈；输出节点7
13. 此时节点6的右子树访问完毕，左右树全部访问完毕，则节点6出栈；输出节点6
14. 此时节点4的右子树访问完毕，左右树全部访问完毕，则节点4出栈；输出节点4
15. 对应输出顺序为1->3->2->5->7->6->4；

三、代码实现遍历

3.1 POJO代码

	public class Node {private int value;private Node leftNode;private Node rightNode;public Node(int value) {this.value = value;}public int getValue() {return value;}public void setValue(int value) {this.value = value;}public Node getLeftNode() {return leftNode;}public void setLeftNode(Node leftNode) {this.leftNode = leftNode;}public Node getRightNode() {return rightNode;}public void setRightNode(Node rightNode) {this.rightNode = rightNode;}}

public static Node createBaseNode() {Node node4 = new Node(4);Node node2 = new Node(2);Node node1 = new Node(1);Node node3 = new Node(3);Node node6 = new Node(6);Node node5 = new Node(5);Node node7 = new Node(7);node4.leftNode = node2;node2.leftNode = node1;node2.rightNode = node3;node4.rightNode = node6;node6.leftNode = node5;node6.rightNode = node7;return node4;}

3.1 前序遍历代码

private static List<Integer> preOrder(Node baseNode, boolean hasNull) {List<Integer> preOrderList = new LinkedList<>();preOrderExecute(preOrderList, baseNode, hasNull);return preOrderList;}private static void preOrderExecute(List<Integer> preOrderList, Node baseNode, boolean hasNull) {if (baseNode == null) {if (hasNull) {preOrderList.add(null);}return;}preOrderList.add(baseNode.value);preOrderExecute(preOrderList, baseNode.leftNode, hasNull);preOrderExecute(preOrderList, baseNode.rightNode, hasNull);}

3.2 中序遍历代码

private static List<Integer> inorderTraversal(Node baseNode, boolean hasNull) {List<Integer> inorderTraversalList = new LinkedList<>();inorderTraversalExecute(inorderTraversalList, baseNode, hasNull);return inorderTraversalList;}private static void inorderTraversalExecute(List<Integer> inorderTraversalList, Node baseNode, boolean hasNull) {if (baseNode == null) {if (hasNull) {inorderTraversalList.add(null);}return;}inorderTraversalExecute(inorderTraversalList, baseNode.leftNode, hasNull);inorderTraversalList.add(baseNode.value);inorderTraversalExecute(inorderTraversalList, baseNode.rightNode, hasNull);}

3.3 后序遍历代码

 private static List<Integer> postorderTraversal(Node baseNode, boolean hasNull) {List<Integer> postorderTraversalList = new LinkedList<>();postorderTraversalExecute(postorderTraversalList, baseNode, hasNull);return postorderTraversalList;}private static void postorderTraversalExecute(List<Integer> postorderTraversalList, Node baseNode, boolean hasNull) {if (baseNode == null) {if (hasNull) {postorderTraversalList.add(null);}return;}postorderTraversalExecute(postorderTraversalList, baseNode.leftNode, hasNull);postorderTraversalExecute(postorderTraversalList, baseNode.rightNode, hasNull);postorderTraversalList.add(baseNode.value);}

这篇关于【 二叉树前中后序遍历】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---