本文主要是介绍一文读懂数字信号处理中的汉明编码Hamming Coding,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、什么是汉明编码?
汉明编码(Hamming Coding)属于前向纠错编码(Forword Error Correction Coding)的一种,除汉明编码外,前向纠错编码通常还包括BCH码,Reed-solomon(RS)码,卷积编码等。前向纠错编码技术通常分为两部分,一是在发射端,对信源进行编码,二是在接收端,对接收数据进行解码、检错、纠错。
二、汉明编码是如何纠错的?
汉明编码也可归类为一种线性分组码,例如最常用的汉明码(7,4),指的就是把原始信息比特每4个比特为一个小的分组,在汉明编码时,对每个分组进行编码,而不是对每个比特进行编码,编码后,每个小组的比特数从4变成7,亦即增加了3bit的数据,用于检错和纠错。
现在将原始4bit信息表示为,而汉明编码产生的3bit监督位表示为
,原始的4bit信息,是分组而来,也就是在汉明编码前,需要将数据每4bit分为一组。而3bit的监督位,则是根据以下规则产生的:
规则R1
规则R2
规则R3
其中,表示异或运算。根据以上三个规则,可以算得全部的原始信息位所对应的监督位的值,如表1所示。

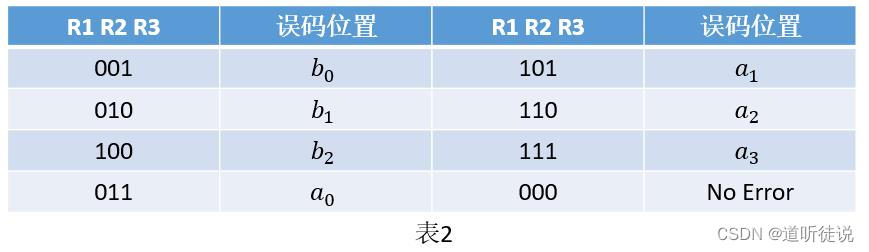
在编码的时候,即可以根据上述的3个规则来产生监督位,Hamming编码的过程,其实可以分为两步,一是将待编码数据按要求先分组,二是根据规则利用原始信息产生监督信息。在解码的时候,需要同样根据这3个规则,来判断到底是是否有错,到底是哪个比特出了错。表2中R1R2R3分别表示规则1、规则2、规则3,满足对应的规则,则值为0,不满足则值为1。通过计算接收的7bit的数据之间是否满足规则R1R2R3,就可以知道是哪个bit在传输的时候出错。换种说法就是,编码后的7bit数据,每个bit和其它几个bit是有关联的,这个关联就是上面所述的规则R1R2R3,从是否满足规则R1R2R3推导出出错的bit。知道了哪个bit出错了之后,直接将出错的bit取反即可实现纠错。从这也可以看出,(7,4)hamming码只能实现1bit的纠错。
接下来,举一个简单的例子来再次说明一下(7,4)Hamming 编码的原理。例如,分组后,得到的4bit原始数据为=[1 0 1 1],然后根据规则R1R2R3(懒得计算可参考表1),计算得到监督位为
=[0 0 1]。从而编码后,得到7bit的数据为[1011 001]。假设在数据传输过程中,有1个bit传输出错,数据从[1011 001]变成了[1010 001],这时候,在解码的时候,根据接收的数据[1010 001],代入规则R1R2R3中计算,
规则R1
规则R2
规则R3
从上面的计算可以发现,数据bit之间的关系满足规则R1,但不满足规则R2、R3。满足规则R1,说明b2,a3,a2,a1是对的,从而在假设错1bit的情况下,如果同时不满足规则R2和R3,就可以知道是bit a0出错了,对比表2中R1R2R3=001时,也可推断是bit a0出错了。知道是bit a0出错,将bit a0取反,可以得到[1011 001],从而实现数据的纠错。
以上即为个人在学习Hamming(7,4)编码时的一些总结,分享到这里,如有理解错误,还望指正,虚心接收大神们的指导。
这篇关于一文读懂数字信号处理中的汉明编码Hamming Coding的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






