本文主要是介绍437.路径总和III,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

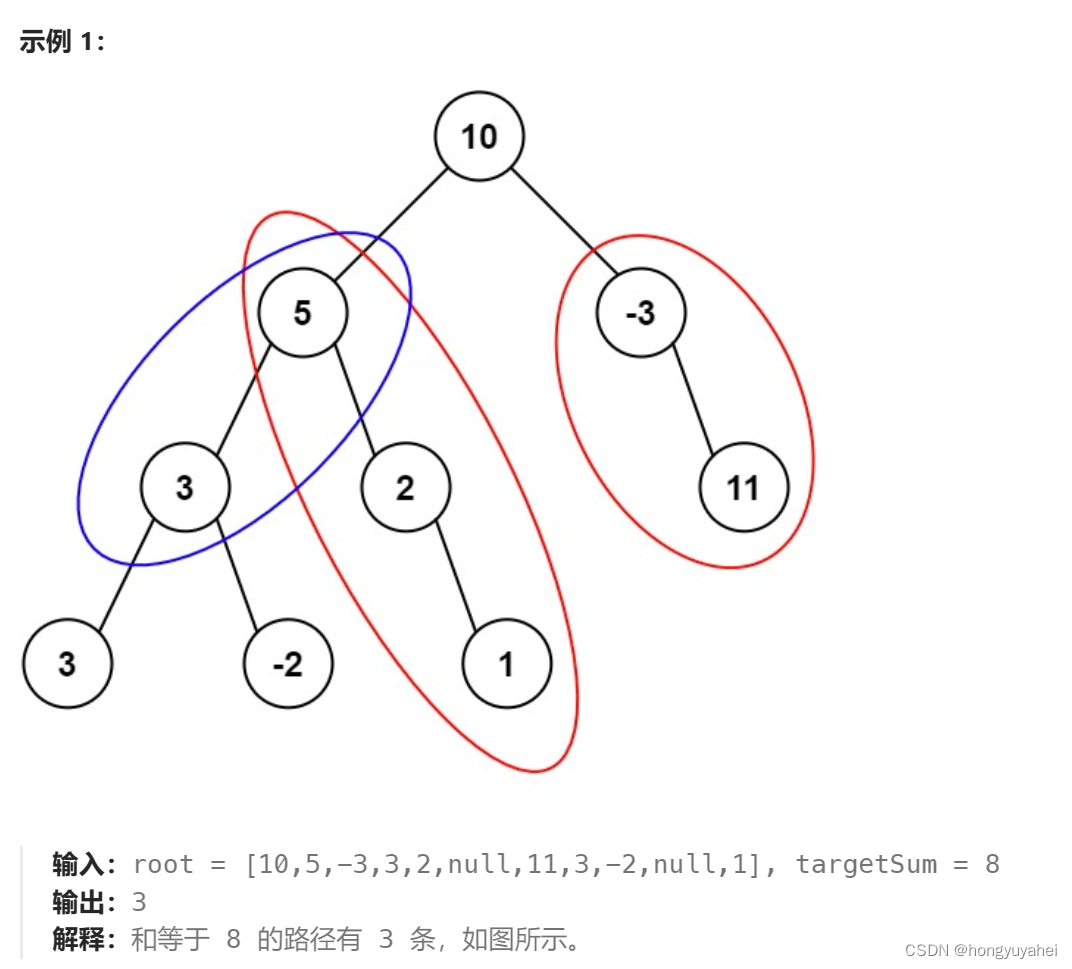

法一:深度优先遍历,递归
- rootSum(p,val)计算节点p向下且路径和为val的路径和
- rootSum(p,val)=rootSum(p->left,val-pval)+rootSum(p->right,val-pval)
- 遍历二叉树所有节点的rootSum并求和
class Solution {
public:int rootSum(TreeNode* node,long target){if(!node){return 0;}int ret=0;int val=node->val;if(val==target){++ret;}ret+=rootSum(node->left,target-val);ret+=rootSum(node->right,target-val);return ret;}int pathSum(TreeNode* root, int targetSum) {if(!root){return 0;}int ret=0;ret=rootSum(root,targetSum);ret+=pathSum(root->left,targetSum);ret+=pathSum(root->right,targetSum);return ret;}
};
法二:前缀和+深度优先遍历
- 根节点root到node的前缀和sum
- 已保存的前缀和中查找是否存在curr-target
class Solution {
public:unordered_map<long long,int>prefix;int dfs(TreeNode* node,long long sum,int target){if(!node) return 0;int ret=0;sum+=node->val;if(prefix.count(sum-target)){ret=prefix[sum-target];}++prefix[sum];ret+=dfs(node->left,sum,target);ret+=dfs(node->right,sum,target);--prefix[sum];return ret;}int pathSum(TreeNode* root, int targetSum) {prefix[0]=1;return dfs(root,0,targetSum);}
};
这篇关于437.路径总和III的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






