算法竞赛入门【码蹄集进阶塔335题】(MT2251-2270）

本文主要是介绍算法竞赛入门【码蹄集进阶塔335题】(MT2251-2270），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

算法竞赛入门【码蹄集进阶塔335题】(MT2251-2270）

文章目录

算法竞赛入门【码蹄集进阶塔335题】(MT2251-2270）
前言
- - 为什么突然想学算法了？
  - 为什么选择码蹄集作为刷题软件？
目录
- 1. MT2251 讲价
- 2. MT2252 复数类1
- 3. MT2253 复数类2
- 4. MT2254 复数类3
- 5. MT2255 复数类4
- 6. MT2256 约数个数
- 7. MT2257 约数之和
- 8. MT2258 有一个计数问题
- 9. MT2259 tax
- 10. MT2260 数树
- 11. MT2261 循环
- 12. MT2262 全部相同
- 13. MT2263 石头剪刀布
- 14. MT2264 异或
- 15. MT2265 除法
- 16. MT2266 除法2
- 17. MT2267 余数之和
- 18. MT2268 大整数乘法
- 19. MT2269 模数
- 20. MT2270 约数个数
- 结语

前言

在这里插入图片描述

为什么突然想学算法了？

> 用较为“官方”的语言讲，是因为算法对计算机科学的所有分支都非常重要。在绝大多数的计算机科学分支领域中，要想完成任何实质性的工作，理解算法的基础知识并掌握与算法密切相关的数据结构知识是必不可少的。
> 但从实际而言，是因为当下快到了考研和找工作的年纪(ಥ_ಥ)，无论走哪一条路，都不免需要一些相对丰富的算法知识，是故，便产生了一个暑假速成算法的计划，可能对于像我这种算法竞赛小白而言，几乎很难，但我仍然还是想尝试一下，毕竟，梦想还是要有的，万一实现了呢？～(￣▽￣～)~

在这里插入图片描述

为什么选择码蹄集作为刷题软件？

码蹄集，是在全国高等学校计算机教学与产业实践资源建设专家委员会(TIPCC) 指导下建设的，其依托全国各大名校计算机系和清华大学出版社等单位的强大资源，旨在为计算机学习爱好者提供全面和权威的计算机习题。


MOD = 10**9+7def pow_mod(a,k,p):ans=1pow_val = a%pwhile k!=0:if k&1 !=0:ans = (ans*pow_val)%ppow_val = (pow_val**2)%pk>>=1return ansdef main():s = input()n = len(s)arr = [ord(ch)-ord('0') for ch in s]pow_v = n-1ans = 0S = 0for i in range(n):if i>=1:ans+=(arr[i]*((i+1)*i//2))*pow_mod(10,pow_v,MOD)ans %=MODk = (n-1)-i+1ans+=(k*S)*pow_mod(10,pow_v,MOD)ans%=MODS+=arr[i]pow_v-=1print(ans)if __name__ == '__main__':main();

2. MT2252 复数类1

（1）题目描述

请你创建一个复数类，在本题中要求实现复数类的读入和输出。

本题测试数据中，读入时不一定是最简(行首正实数前面可能有”+”号)，但输出时要求最简。

最简情况是:实数直接表示，虚数以”a+bi”(其中”+”号也可能是”-“号，且a若为0则不显示，b若为1则不显示，基本和书面写法一样，可参考样例)的格式表示。

格式

输入格式:
第一行输入一个整数n,n表示数据组数。
接下来n行，每行输入一个复数（以类似”a+bi”的格式输入，但不一定最简，可能会有多个项，输入的项的系数是浮点数)。
.
输出格式:
输出n行，按题目描述中“最简情况”输出读入得到的复数，浮点数用cout或printf( "%g”)输出。

样例1

输入:
8
123
0i
i
i+3
3-i
7.6+1i
76.7-0.66i
3i+7i+8i+9+0+03.67i+10
.
输出:
123
0
i
3+i
3-i
7.6+i
76.7-0.66i
19+21.67i

备注：

可以借助C++的STL中的complex头文件。浮点数请使用double类型。保证:对于100%的数据: 1≤n ≤100,000，每行输入非空字符串长度不超过1000，输入的浮点数最多精确到小数点后两位。

（2）参考代码

#include<bits/stdc++.h>
using namespace std;int n;
complex<double> c;void inputComplex(complex<double> &cplx){bool sgn,inpnum;double num,dec;cplx.real(0);cplx.imag(0);char x = getchar();while(x!='-'&&x!='i'&&(x<'0'||x>'9')) x=getchar();while(x=='-' || x=='+' || x=='i' || (x>='0'&&x<='9')){sgn=0;if(x=='-'){sgn=1;x=getchar();}else if(x=='+') x=getchar();num=0;inpnum = false;while(x>='0'&&x<='9'){inpnum = true;num *= 10;num += x-'0';x = getchar();}if(x=='.'){x = getchar();dec = 1;while(x>='0'&&x<='9'){dec /= 10;num += dec*(x-'0');x = getchar();}}if(x=='i'){if(!inpnum) cplx.imag(cplx.imag()+sgn?-1:1);else cplx.imag(cplx.imag()+(sgn?-num:num));x = getchar();}else cplx.real(cplx.real()+(sgn?-num:num));}
}void outputComplex(complex<double> cplx){if(cplx.imag()==0) cout<<cplx.real();else{if(cplx.real()==0){if(cplx.imag()==1) cout<<'i';else if(cplx.imag()== -1) cout<<"-i";else cout<<cplx.imag()<<"i";}else{if(cplx.imag()==1) cout<<cplx.real()<<"+i";else if(cplx.imag()==-1) cout<<cplx.real()<<"-i";else cout<<cplx.real()<<showpos<<cplx.imag()<<noshowpos<<"i";}}
}complex<double> conjugateComplex(complex<double> cplx){cplx.imag(-cplx.imag());return cplx;
}int main()
{   scanf("%d",&n);while(n--){inputComplex(c);outputComplex(c);printf("\n");}return 0;
}

3. MT2253 复数类2

（1）题目描述
请你创建一个复数类，在本题中要求实现复数类的求共辄复数和求模操作。

做本题之前，最好先完成同系列题目《复数类1》，本题的复数输入输出要求与相同。

格式

输入格式:
第一行输入一个整数n,n表示数据组数。接下来n行，每行输入一个复数。
.
输出格式: 输出n行，每一行对于其输入的复数，输出其共辄复数和模，以空格隔开。

样例1

输入:
8
123
0i
i
i+3
3-i
7.6+1i
76.7-0.66i
3i+7i+8i+9+0+03.67i+10
.
输出:
123 123
0 0
-i 1
3-i 3.16228
3+i 3.16228
7.6-i 7.66551
76.7+0.66i 76.7028
19-21.67i 28.8199

（2）参考代码

#include<bits/stdc++.h>
using namespace std;int n;
complex<double> c;void inputComplex(complex<double> &cplx){bool sgn, inpnum;	//0:pos, 1:negdouble num, dec;	//num:读入的数(不含符号位), dec:decimal小数点后的cplx.real(0);		//先初始化实部虚部为0cplx.imag(0);char x = getchar();	//开始读取while (x!='-'&&x!='i'&&(x<'0'||x>'9')) x = getchar();	//不读取无关符号while (x=='-'||x=='+'||x=='i'||(x>='0'&&x<='9')){	//当读取到了有关符号，若读取到无关符号再退出循环sgn = 0;		//一开始符号位为正if (x=='-'){	//读取符号位sgn = 1;x = getchar();}else if (x=='+')	x = getchar();num = 0;		//一开始数字位为0inpnum = false;	//用于判断是否输入了数字，用于判断"i"前无数字的特殊情况while (x>='0'&&x<='9'){	//读取数字inpnum = true;num *= 10;num += x-'0';x = getchar();}if (x=='.'){			//读取小数点后数字x = getchar();dec = 1;while (x>='0'&&x<='9'){dec /= 10;num += dec*(x-'0');x = getchar();}}if (x=='i'){			//通过结尾是不是"i"来判断读取的是实数还是虚数if (!inpnum) cplx.imag(cplx.imag()+(sgn?-1:1));//若"i"前无数字，系数为1else cplx.imag(cplx.imag()+(sgn?-num:num));x = getchar();}else	cplx.real(cplx.real()+(sgn?-num:num));}
}void outputComplex(complex<double> cplx){if (cplx.imag() == 0) cout<<cplx.real();	//使用输出流，输出最简小数else{if (cplx.real() == 0){if (cplx.imag() == 1) cout<<'i';else if (cplx.imag() == -1) cout<<"-i";else cout<<cplx.imag()<<'i';}else{if (cplx.imag() == 1) cout<<cplx.real()<<"+i";else if (cplx.imag() == -1) cout<<cplx.real()<<"-i";else cout<<cplx.real()<<showpos<<cplx.imag()<<noshowpos<<'i';//第二个复数保留前导'+'}}
}complex<double> conjugateComplex(complex<double> cplx){cplx.imag(-cplx.imag());return cplx;
}double modulusComplex(complex<double> cplx){double r = cplx.real(), i = cplx.imag();return sqrt(r*r+i*i);
}int main(){scanf("%d",&n);while (n--){inputComplex(c);outputComplex(conjugateComplex(c));cout<<' '<<modulusComplex(c)<<endl;}return 0;
}

4. MT2254 复数类3

（1）题目描述
请你创建一个复数类，在本题中要求解决复数类的求和问题。

做本题之前，最好先完成同系列题目《复数类1》，本题的复数输入输出要求与其相同。

格式

输入格式:
第一行输入一个整数n,n表示数据组数。接下来n行，每行输入一个复数。
.
输出格式: 输出一行一个最简复数，为输入的n个复数的总和。

样例1：

输入：
8
123
0i
i
i+3
3-i
7.6+1i
76.7-0.66i
3i+7i+8i+9+0+03.67i+10
.
输出：232.3+23.01i

（2）参考代码

#include<bits/stdc++.h>using namespace std;const int N = 1e5 + 10;int n;double x, y;complex<double> ans;int main( ){ios::sync_with_stdio(false);cin.tie(0);cin >> n;string s;for (int i = 0; i < n; i++) {cin >> s;int j = 0, m = s.size(), last = 0, lastop = 1;if (s[0] == '-' || s[0] == '+') {lastop = s[0] =='-' ? -1: 1;s = s.substr(1);}while (j <= m) {if (j == m || s[j] == '+' || s[j] == '-') {string t = s.substr(last, j - last);complex<double> tc;if (t.back() == 'i') {if (t.size() == 1) tc.imag(lastop);else tc.imag(stod(t.substr(0, t.size() - 1)) *lastop);}else tc.real(stod(t) * lastop);ans += tc;last = j + 1;if (j < m)lastop = s[j] == '+' ? 1: -1;}j ++;}}if (ans.real() != (double)0) cout << ans.real();if (ans.real() && ans.imag() > 0) cout << "+";if (ans.imag() != (double)1 && ans.imag() != (double)0) cout <<ans.imag();if (ans.imag() != (double)0) cout << "i";return 0;}

5. MT2255 复数类4

（1）题目描述
请你创建一个复数类，在本题中要求实现复数类的四则运算即加法、减法、乘法、除法。

做本题之前，最好先完成同系列题目《复数类1》，本题的复数输入输出要求与其相同。

格式

输入格式:

.
输出格式: 对于每行四则运算表达式，输出一行表达式返回的结果复数。

样例1

输入:
4
123 )+( 0i
i )-( i+3
3-i )*( 7.6+1i
76.7-0.66i )/( 3i+7i+8i+9+0+03.67i+10
.
输出:
123
-3
23.8-4.6i
1.73732-2.01619i

备注：

其中: 1≤m ≤le8,1 ≤n ≤1e10

（2）参考代码

#include<bits/stdc++.h>
using namespace std;void inputComplex(complex<double> &cplx){bool sgn, inpnum; //0:pos, 1:negdouble num, dec; //num:读入的数(不含符号位), dec:decimal小数点后的cplx.real(0);  //先初始化实部虚部为0cplx.imag(0);char x = getchar(); //开始读取while (x!='-'&&x!='i'&&(x<'0'||x>'9')) x = getchar(); //不读取无关符号while (x=='-'||x=='+'||x=='i'||(x>='0'&&x<='9')){ //当读取到了有关符号，若读取到无关符号再退出循环sgn = 0;  //一开始符号位为正if (x=='-'){ //读取符号位sgn = 1;x = getchar();}else if (x=='+') x = getchar();num = 0;  //一开始数字位为0inpnum = false; //用于判断是否输入了数字，用于判断"i"前无数字的特殊情况while (x>='0'&&x<='9'){ //读取数字inpnum = true;num *= 10;num += x-'0';x = getchar();}if (x=='.'){   //读取小数点后数字x = getchar();dec = 1;while (x>='0'&&x<='9'){dec /= 10;num += dec*(x-'0');x = getchar();}}if (x=='i'){   //通过结尾是不是"i"来判断读取的是实数还是虚数if (!inpnum) cplx.imag(cplx.imag()+(sgn?-1:1));//若"i"前无数字，系数为1else cplx.imag(cplx.imag()+(sgn?-num:num));x = getchar();}else cplx.real(cplx.real()+(sgn?-num:num));}
}void outputComplex(complex<double> cplx){if (cplx.imag() == 0) cout<<cplx.real(); //使用输出流，输出最简小数else{if (cplx.real() == 0){if (cplx.imag() == 1) cout<<'i';else if (cplx.imag() == -1) cout<<"-i";else cout<<cplx.imag()<<'i';}else{if (cplx.imag() == 1) cout<<cplx.real()<<"+i";else if (cplx.imag() == -1) cout<<cplx.real()<<"-i";else cout<<cplx.real()<<showpos<<cplx.imag()<<noshowpos<<'i';//第二个复数保留前导'+'}}
}int n;
complex<double> a,b;
char k[5];int main(){scanf("%d",&n);while (n--){inputComplex(a);scanf("%s",k);inputComplex(b);if (strcmp(k,")+(") == 0) outputComplex(a+b);else if (strcmp(k,")-(") == 0) outputComplex(a-b);else if (strcmp(k,")*(") == 0) outputComplex(a*b);else if (strcmp(k,")/(") == 0) outputComplex(a/b);putchar('\n');}return 0;
}

6. MT2256 约数个数

（1）题目描述
给出给定正整数n，求n的约数个数。

格式

输入格式: 一个整数n。
.
输出格式: 输出一行一个整数表示答案。

样例1

输入: 12
.
输出: 6

备注：

其中: 1≤n ≤1e9

（2）参考代码


#include <bits/stdc++.h>
using namespace std;
int a,ans;
inline int read()
{int f=1,x=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return f*x;
}
int main()
{a=read();for(int i=1;i<=a/i;i++){if(a%i==0){ans++;if(a/i!=i){ans++;    }    }    }printf("%d\n",ans);return 0;
}

7. MT2257 约数之和

（1）题目描述
给出给定正整数n，求n的约数之和。

格式

输入格式: 一个整数n。
.
输出格式: 输出一行一个整数表示答案。

样例1

输入: 12
.
输出: 28

备注：

其中: 1≤n ≤1e6

（2）参考代码


import java.util.Scanner;
class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int count = 0;for (int i = 1; i <= n; i++) {if (n % i == 0) {count += i;}}System.out.println(count);}
}

8. MT2258 有一个计数问题

（1）题目描述
给予两个数a,b，进行q次询问。对于每次询问，你需要回答:在1,r]中，满足以下条件的x的个数: (a mod a) mod b ≠ (a mod b) mod a，注意有多组数据输入。

格式

输入格式: 第一行一个数T表示数据组数，每一组数据，第一行为a,b, q ,接下来q行为q个询问。
.
输出格式: 对每个询问输出答案，以空格分隔，无需换行。

样例1

输入:
2
4 6 5
1 1
1 3
1 5
1 7
1 9
7 10 2
7 8
100 200
.
输出: 0 0 0 2 4 0 91

备注：

其中:1≤T ≤100,1 ≤ a, b ≤200,1 ≤q≤500,1 ≤l≤r ≤1e9。

（2）参考代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int T;int main(){scanf("%d",&T);while(T--){ll a,b,q;cin>>a>>b>>q;if(a<b) swap(a,b);ll lcm = a*b / __gcd(a,b);ll len = lcm-a;while(q--){ll ans = 0;ll l,r;cin>>l>>r;ll x = r/lcm-l/lcm;ans += x*len;r %= lcm;if(r>=a) ans+=r-a+1;l%=lcm;if(l>a) ans -= l-a;cout<<ans<<' ';}}return 0;
}

9. MT2259 tax

（1）题目描述
小码哥要交税，交的税钱是收入n的最大因子(该最大因子为不等于n的最大因子)，但是现在小码哥为了避税，把钱拆成几份（每份至少为2)，使交税最少，输出税钱。

格式

输入格式: 一个正整数n表示所有的钱数。
.
输出格式: 输出一个正整数，表示税钱。

样例1

输入: 4
.
输出: 2

（2）参考代码


#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
using namespace std;int n;int main(){while(scanf("%d",&n)!=EOF){int k = sqrt(n);bool flag = false;for(int i = 2; i <= k; i ++){if(n % i == 0){flag = true;break;}}if(!flag) printf("1\n");else{if(n % 2 == 0) printf("2\n");else{int t = n - 2;int kk = sqrt(t);flag = false;for(int i = 2; i <= kk; i ++){if(t % i == 0){flag = true;break;}}if(flag) printf("3\n");else printf("2\n");}}}return 0;
}

10. MT2260 数树

（1）题目描述
在卡兹戴尔有一片很奇怪的森林，在一个直角坐标系内的(a, g)坐标值都为自然数的坐标上都有一颗树，如果一棵树的坐标(z, gj）与原点(0,0)的连线中没有通过其他任何树，则称该树在原点处是可见的。

例如，树 (4,2)就是不可见的，因为它与原点的连线会通过树(2,1)。

部分可见点与原点的连线如下图所示，如图是一个4×4的树林。

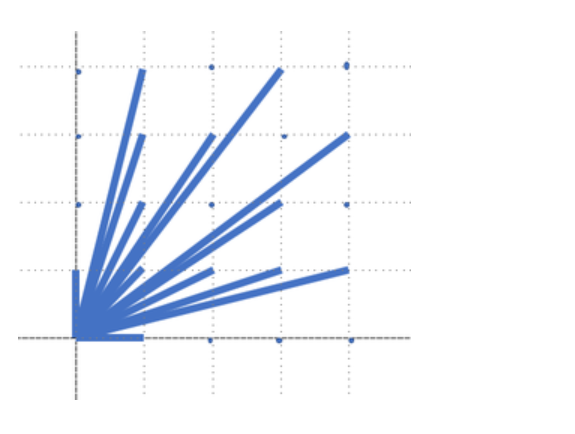
在这里插入图片描述

请你计算出在一个 n xn 的树林中可见的树有多少。

格式

输入格式:
第一行包含整数C，表示共有C 组测试数据。每组测试数据占一行，包含一个整数N。
.
输出格式: 每组测试数据的输出占据一行。分别为测试数据的编号(从1开始），该组测试数据对应的N以及可见点的数量。同行数据之间用空格隔开。

样例1

输入:
4
2
4
5
231
.
输出:
1 2 5
2 4 13
3 5 21
4 231 32549

备注：

提示:0≤a,9 ≤n,1≤N ≤2000,1 ≤C≤10。

（2）参考代码


#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\n",a,b);
typedef long long ll;
using namespace std;inline int read(){int s=0,w=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);return s*w;
}
const int maxn=5e4+9;
int prime[maxn],cnt;
bool st[maxn];
int phi[maxn];
void init(int n){phi[1]=1;for(int i=2;i<=n;i++){if(!st[i]){prime[cnt++]=i;phi[i]=i-1;}for(int j=0;prime[j]*i<=n;j++){st[prime[j]*i]=1;if(i%prime[j]==0){phi[i*prime[j]]=phi[i]*prime[j];break;}phi[i*prime[j]]=phi[i]*(prime[j]-1);}}
}
int main()
{init(maxn-1);int n,m;cin>>m;for(int T=1;T<=m;T++){cin>>n;int res=1;//对角线那个 for(int i=1;i<=n;i++)res+=phi[i]*2;cout<<T<<" "<<n<<" "<<res<<endl; }return 0;
}

11. MT2261 循环

（1）题目描述
给定c, g, k，求ac/y在k进制下是否为纯循环小数，当ac /y为整数时我们也当作纯循环小数。

格式

输入格式: 三个正整数c，y，k
.
输出格式: 输出YES或者NO

样例1

输入: 4 8 3
.
输出: YES

备注：

其中: a, 3 ≤1000000，2≤k ≤1000000

（2）参考代码

#include<bits/stdc++.h> 
using namespace std;
int x,y,k,d;
int main( )
{cin>>x>>y>>k;d=__gcd(x,y);x/=d,y/=d;int cnt(0);while(1){d=__gcd(y,k);if(d==1)break;y/=d;++cnt;}if(y==1||cnt)cout<<"NO"<<endl;else cout<<"YES"<<endl;return 0;
}

12. MT2262 全部相同

（1）题目描述
小码哥有一个n个整数组成的数组a1, a2,… . , an。小码哥可以任取一个正整数k，进行下面的操作:从数列中取一个数ai，将它的值减去k。小码哥进行了若干次(可能是0次）上面的操作后，数列中所有的数都相等了。请你找到k可能的最大值。

格式

输入格式:
多组输入，第一行包含一个整数t (1≤t≤104 )，代表测试样例组数，下面2t行，每2行一组，每组第一行为数列的长度n ( 4≤n ≤40 )，第二行n个整数a1, a2,. . . , an ( -106 ≤a;≤106 )。
.
输出格式: 对于每组输入输出一行k的最大值（如果k可以任意大，输出-1 )。

样例1

输入:
3
6
1 5 3 1 1 5
8
-1 0 1 -1 0 1 -1 0
4
100 -1000 -1000 -1000
.
输出:
2
1
1100

（2）参考代码

#include <bits/stdc++.h>
using namespace std;int t;
int n;
long long a[41];int main()
{cin>>t;while(t--){cin>>n;long long min_num=1e6+1;for(int i=1;i<=n;i++){cin>>a[i];min_num=min(min_num,a[i]);}long long g=0;for(int i=1;i<=n;i++){if(a[i]!=min_num){if(g==0){g=a[i]-min_num;}else{g=__gcd(g,a[i]-min_num);}}}if(!g){cout<<"-1"<<endl;}else{cout<<g<<endl;}}
}

13. MT2263 石头剪刀布

（1）题目描述
有两个人在玩石头剪刀布游戏:R-石头P-布S-剪刀每个人都会按照一个周期出石头，剪刀或布。周期肯定在1000以内（包括1000）问玩n把后，双方各输了多少次。

格式

输入格式:
输入第一行一个n，( 1<n≤2* 109 ) n为玩了几把，第2行为第一个人的周期规律，第3行为第二个人的周期规律。
.
输出格式: 输出共2个数:第一个人输的次数和第二个人输的次数。

样例1

输入:
7
RPS
RSPP
.
输出: 3 2

（2）参考代码

#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=1000010;
const int M=1e6+1005;
const int mod=1e9+7;
int n;
char a[N],b[N];
char A[N],B[N];
void work() {cin>>n;cin>>a+1;cin>>b+1;int lena=strlen(a+1),lenb=strlen(b+1);for(int i=1;i<=lenb;i++) {for(int j=1;j<=lena;j++) {A[(i-1)*lena+j]=a[j];}}for(int i=1;i<=lena;i++) {for(int j=1;j<=lenb;j++) {B[(i-1)*lenb+j]=b[j];}}int lenc=lena*lenb,suma=0,sumb=0;for(int i=1;i<=lenc;i++) {if(A[i]=='R'&&B[i]=='P') suma++;if(A[i]=='P'&&B[i]=='S') suma++;if(A[i]=='S'&&B[i]=='R') suma++;if(B[i]=='R'&&A[i]=='P') sumb++;if(B[i]=='P'&&A[i]=='S') sumb++;if(B[i]=='S'&&A[i]=='R') sumb++;}int num=n/lenc;suma=suma*num; sumb=sumb*num;n %= lenc;for(int i=1;i<=n;i++) {if(A[i]=='R'&&B[i]=='P') suma++;if(A[i]=='P'&&B[i]=='S') suma++;if(A[i]=='S'&&B[i]=='R') suma++;if(B[i]=='R'&&A[i]=='P') sumb++;if(B[i]=='P'&&A[i]=='S') sumb++;if(B[i]=='S'&&A[i]=='R') sumb++;}cout<<suma<<" "<<sumb<<endl;
}
signed main() {work();return 0;
}

14. MT2264 异或

（1）题目描述
给定一个正整数n，在[1,n]的范围内，求出有多少个无序数对(a,b)满足gcd(a,b) = acorb。其中gcd(a,b)表示a,b的最大公约数，而acorb表示α异或b。

格式

输入格式: 输入共一行，一个正整数n。
.
输出格式: 一个数ans，表示答案。

样例1

输入: 3
.
输出: 1

（2）参考代码

#include <bits/stdc++.h>
using namespace std;
int f[10000001];
int main()
{int n;cin>>n;for(int i=1;i<=5000000;i++){for(int j=i*2;j<10000000;j+=i){int b=j-i;if((j^b)==i) f[j]++;}}for(int i=1;i<=n;i++) f[i]+=f[i-1];cout<<f[n];
}

15. MT2265 除法

（1）题目描述
给出给定正整数n，求n的约数个数。

格式

输入格式: 一个整数n。
.
输出格式: 一个数表示答案

样例1

输入: 4
.
输出: 8

备注：

其中: n≤1000000000

（2）参考代码

#include<bits/stdc++.h> using namespace std;
typedef long long ll;//整数分块
int main( )
{ll n,sum=0;cin>>n;for(int i=1,r;i<=n;i=r+1){r = n/(n/i);sum += (r-i+1)*(n/i);}cout<<sum;return 0;
}

16. MT2266 除法2

（1）题目描述
给出给定正整数n，求n的约数个数。

格式

输入格式: 一个正整数n。
.
输出格式: 一个数表示答案。

样例1

输入: 4
.
输出: 15

备注：

其中: n≤1000000。

（2）参考代码

#include<bits/stdc++.h> using namespace std;
typedef long long ll;//整数分块
int main( )
{ll n,sum=0;cin>>n;for(int i=1,r;i<=n;i=r+1){r = n/(n/i);sum += (r-i+1)*(n/i)*(i+r)/2;}cout<<sum;return 0;
}

17. MT2267 余数之和

（1）题目描述
你上次很轻松的解决了小码哥的问题，这让小码哥觉得很没面子，于是他又想了一个更加复杂的问题来考你。

小码哥给你两个正整数n和f，计算judge(n,f)=f的值，其中f表示f除以i的余数。

格式

输入格式: 输入仅一行，包含两个正整数n, f。
.
输出格式: 输出仅一行，即judge(n, f )。

样例1

输入: 5 3
.
输出: 7

备注：

其中: 1≤n,f ≤1000000000 。

（2）参考代码

#include<bits/stdc++.h> using namespace std;long long int judge(long long int n,long long int f){long long int res=0;for(long long int i=1;i<=n;i++){res+=f%i;}return res;
}
int main( )
{long long int n,f,num;cin>>n>>f;num=judge(n, f);cout<<num;return 0;
}

18. MT2268 大整数乘法

（1）题目描述
求(a * b)modc 。

格式

输入格式: 三行，依次输入3个整数a,b,c 。
.
输出格式: 一个整数，表示(a * b)modc 的值。

样例1

输入:
2
3
10
.
输出: 6

备注：

提示: 1≤a,b,c<1018

（2）参考代码

#include<stdio.h>unsigned long long mul(unsigned long long a,unsigned long long b,unsigned long long c)
{
unsigned long long int a1=a,b1=b,c1=c;if(!a1)return 0;return (((a1&1)*b1)%c1+(mul(a1>>1,b1,c1)<<1)%c1)%c1;
}int main() 
{ long long int a, b, c,res;  scanf("%lld",&a);scanf("%lld",&b);scanf("%lld",&c);res=mul(a, b, c);printf("%lld",res);return 0; 
}

19. MT2269 模数

（1）题目描述
现在小码哥给定两个整数a, b，问有多少个α，使得满足等式 amoda = b，如果存在无限个，就输出“infinity”，否则输出满足条件x的个数。

格式

输入格式: 两个数a,b。
.
输出格式: 输出个数或"infinity"。

样例1

输入: 21 5
.
输出: 2

备注：

其中:1≤a,b ≤1e9。

（2）参考代码

#include<bits/stdc++.h> using namespace std;int main( )
{int a,b,count=0,value;cin>>a>>b;value=a-b;if(value==0){cout<<"infinity";return 0;}for(int i=1;i<=sqrt(value);++i){if(value%i==0&&value/i>b){if(i>b) count+=2;else ++count;}}cout<<count;return 0;
}

20. MT2270 约数个数

（1）题目描述
小码哥有一天想把20!表示出来，但是小码哥意识到这个数字算出来将非常大，于是你给小码哥出主意，用算术基本定理的形式表示，于是这个任务理所应当的被小码哥推给了你，正好你想干点简单的事来换换脑子，就接受了。你要把N!按照算术基本定理的形式表示。

基本算数定理:一个数一定可以用一下形式表示:

在这里插入图片描述

pi为质数数组，c[üi]为每一个质数的幂的次数。对于不同的x来说，有不同的p和c数组。

格式

输入格式: 输入一个整数N。
.
输出格式: N!分解质因数后的结果，共若干行，每行两个数p,c ,表示含有p项。按照p[i从小到大的顺序输出。

样例1

输入: 5
.
输出:
2 3
3 1
5 1

备注：

样例解释:
5!=54 3* 2* 1 = 23* 31* 51;
3≤N ≤ 1e6。

（2）参考代码


#include <bits/stdc++.h>
using namespace std;
int a,ans;
inline int read()
{int f=1,x=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return f*x;
}
int main()
{a=read();for(int i=1;i<=a/i;i++){if(a%i==0){ans++;if(a/i!=i){ans++;    }    }    }printf("%d\n",ans);return 0;
}