【NOIP2012模拟8.9】逐个击破

题目大意

给定一棵树，其中k个点被标记。现在的任务是破坏掉树上的某些边，使得k个点都属于不同的连通块。

题解

直接的一个想法，就是找到两两的lca，然后取路径上的最小值。
但是这样是$O(n^2)$的。
是否可以像对trie中的字符串进行排序那样来排序这棵树上的k个点？
即每一个点维护一个$L[i]$和$R[i]$，表示i的子树包含了排名为$[l,r]$的被标记的点。
每一次从某个被标记的点x出发向上走，走到L值或R值不同的第一个点y就停下，然后记录$(x,y)$上最小边权。答案累加。
但这样做是错的。
这样子不能够体现任意2个点的LCA，因为父亲的$L$值或$R$值不一样时，有这么几种情况：
比如下面这种情况就是反例。

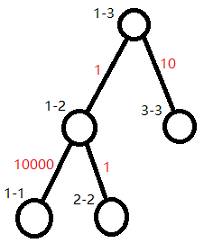
（这显然是反例）
所以正解应该是做一遍最大生成树，当两个待合并的连通块均含有被标记的点时，此边必选。
这样一来，选中的边代表非要选的边的集合的最小的一条，表现出“任意两个标记的点的LCA”。

心得

最重要的，设计的算法要表现出“任意两个标记的点的LCA”。
考虑区间包含的关系。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define N 100010
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fd(i,a,b) for(i=a;i>=b;i--)
using namespace std;
struct note{int x,y,z;
};note a[N];
int head[N],tot;
int l1[N],r1[N],o[N],b[N];
int i,j,k,l,n,m,temp;
long long ans;
int u,v,w;
int bz[N],f[N];
int read(){int res=0,fh=1;char ch;while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();if(ch=='-')fh=-1,ch=getchar();while(ch>='0'&&ch<='9')res=res*10+ch-'0',ch=getchar();return fh*res;
}
void mi(int &x,int y){x=x<y?x:y;}
void ma(int &x,int y){x=x>y?x:y;}
bool cmp(note a,note b){return a.z>b.z;}
int get(int x){return f[x]==x?x:f[x]=get(f[x]);
}
int main(){n=read();m=read();fo(i,1,m)u=read(),u++,bz[u]=1;fo(i,1,n-1){u=read(),v=read(),w=read();u++,v++;a[i].x=u;a[i].y=v;a[i].z=w;}sort(a+1,a+n,cmp);fo(i,1,n)f[i]=i;fo(i,1,n-1){u=get(a[i].x);v=get(a[i].y);if(u!=v){f[v]=u;if(bz[u]&&bz[v])ans+=1ll*a[i].z;bz[u]|=bz[v];}}printf("%lld",ans);return 0;
}