Holographic MIMO Surfaces （HMIMOS）以及Reconfigurable Holographic Surface（RHS）阅读笔记总结

---

---

写在前面

✅给自己提出几个问题？

✒️ 全息智能表面与远进场有何关系，是仅限于毫米波或者太赫兹吗
✒️ 全息智能表面相较于传统大规模MIMO有何优势
📆 全息智能表面的天线间距在仿真中如何设置
📆 全息智能表面与其他方向的结合
📆 matlab绘制全息MIMO表面的波束方向图
📆 类比智能反射面，全息智能表面的固有约束
📆 全系表面与天线孔径

全息MIMO能突破有限物理口径约束下的容量极限吗
给出了自由度、辐射效率和容量极限的计算。

---

Holographic MIMO Surfaces for 6G Wireless Networks: Opportunities, Challenges, and Trends的阅读笔记

https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9136592

摘要

未来的无线网络预计将朝着智能和软件可重构范式发展，从而实现人类和移动设备之间无处不在的通信。它们还能够感知、控制和优化无线环境，以实现低功耗、高吞吐量、大规模连接和低延迟通信的愿景。最近越来越受欢迎的一个关键概念推动因素是 HMIMOS，它是指由亚波长金属或电介质散射颗粒组成的低成本变革性无线平面结构，能够根据所需目标塑造电磁波。在本文中，我们概述了 HMIMOS 通信，包括用于重新配置此类表面的可用硬件架构，并强调了设计支持 HMIMOS 的无线通信的机遇和主要挑战。

简介

未来的无线网络，即第五代 (5G) 和第六代 (6G) 之后的无线网络，需要支持大量用户，满足日益严格的频谱效率 (SE) 和能源效率 (EE) 要求 [1-4]。近年来，无线通信研究对大规模多输入多输出 (MIMO) 系统的兴趣日益浓厚，其中基站 (BS) 配备了大型天线阵列，作为满足 5G 吞吐量要求的创新方式。然而，实现具有真正大规模天线阵列（即数百个或更多天线）的大规模 MIMO 基站仍然是一项非常具有挑战性的任务，主要是由于制造和运营成本较高，以及功耗增加。

未来的6G无线通信系统有望实现智能和软件可重构范式，其中设备硬件的所有部分都将适应无线环境的变化[1,3,5]。支持波束成形的天线阵列、认知频谱使用以及自适应调制和编码是目前可调谐的几个收发器方面，以优化通信效率。然而，在这个优化过程中，无线环境仍然是一个难以管理的因素；它仍然不知道其内部正在进行的通信过程 [1, 3-9]。此外，无线环境通常对无线链路的效率具有有害影响。信号衰减限制了节点的连接半径，而导致衰落现象的多径传播是一个经过充分研究的物理因素，会引起接收信号功率的剧烈波动。信号恶化可能是毫米波和即将推出的太赫兹 (THz) 通信的主要问题之一[1]。

尽管大规模 MIMO、三维 (3D) 波束成形及其硬件高效的混合模拟和数字技术 [10] 提供了出色的方法来通过基于软件的传输方向性控制来抵消无线传播造成的信号衰减，但它们强加了移动性和硬件可扩展性问题。更重要的是，电磁（EM）传播的智能操纵仅部分可行，因为部署区域中的物体（除了收发器）是不可控的。因此，无线环境作为一个整体仍然不知道其内部正在进行的通信，并且信道模型继续被视为概率过程，而不是通过软件控制技术实现的近乎确定性的过程。

随着最近在可编程超材料制造方面取得突破，可重构智能表面有潜力实现 6G 网络的挑战性愿景，并在部署在各种物体表面时实现无线通信系统中的无缝连接和基于智能软件的环境控制[5-8]。*（控制无线信道）*通过利用这一进步，全息 MIMO 表面 (HMIMOS) 旨在超越大规模 MIMO，基于低成本、尺寸、重量和低功耗的硬件架构，为将无线环境转变为可编程智能实体提供了一种变革性的方法。[ 3、5、8、9、11、12]。在本文中，我们概述了不同的新兴 HMIMOS 架构及其核心功能，并讨论了它们当前考虑的通信应用以及未来的网络挑战。

---

HMIMOS模型

在本节中，我们将介绍 HMIMOS 系统的可用硬件架构、制造方法和操作模式，使它们成为各种无线通信应用的灵活可集成概念。

根据功耗分类

可分为

1. 主动： Active HMIMOS
2. 被动：Passive HMIMOS

### 主动
为了实现可重新配置的无线环境，HMIMOS 可以充当发射器、接收器或反射器。

当考虑收发器的作用，从而将能量密集型射频 (RF) 电路和信号处理单元嵌入到表面时，采用术语“active HMIMOS”[13, 14]。另一方面，active HMIMOS 系统是传统大规模 MIMO 系统的自然演变，通过将越来越多的软件控制天线元件封装到有限尺寸的二维 (2D) 表面上。

在[4]中，相邻表面元素之间的间距随着数量的增加而减小，主动 HMIMOS active HMIMOS 也称为大型智能表面Large Intelligent Sur-
face (LIS)。

---

有源 HMIMOS 的实际实施可以是大量微型天线元件与可重构处理网络的紧凑集成，从而实现连续的天线孔径。这种结构可利用全息原理在整个表面上发射和接收通信信号[13, 14]。

另一种有源 HMIMOS 实现可以基于离散光子天线阵列，该天线阵列集成有源光电检测器、转换器和调制器，用于执行光或 RF 信号的传输、接收和转换 [13]。

### 被动
无源 HMIMOS （Passive HMIMOS），也称为可重新 配置智能表面Reconfi gurable Intelligent Surface (RIS) [3, 5–7, 9] 或智能反射表面 Intelligent Reflecting Surface(IRS) [8, 15]，其作用类似于无源金属镜或“波收集器”，并且可以可以通过编程来以可定制的方式改变撞击的电磁场 [3, 5]。与有源 HMIMOS 相比，无源 HMIMOS 通常由不需要专用电源的低成本无源元件组成。它们的电路和嵌入式传感器可以通过能量收集模块供电，这种方法有可能使它们真正实现能源中和。无论其具体实现如何，从能耗角度来看，无源 HMIMOS 技术之所以具有吸引力，是因为它们能够对撞击到的无线电波进行整形并转发输入信号，而无需使用任何功率放大器或 RF 链，也无需应用复杂的信号加工。此外，无源HMIMOS可以在全双工模式下工作，而不会产生明显的自干扰或增加的噪声水平，并且仅需要低速率控制链路或回程连接。最后，无源 HMIMOS 结构可以轻松集成到无线通信环境中，因为其极低的功耗和硬件成本使它们能够部署到建筑物外墙、房间和工厂天花板、笔记本电脑外壳甚至人类衣服中 [3, 5] 。

基于硬件结构的分类

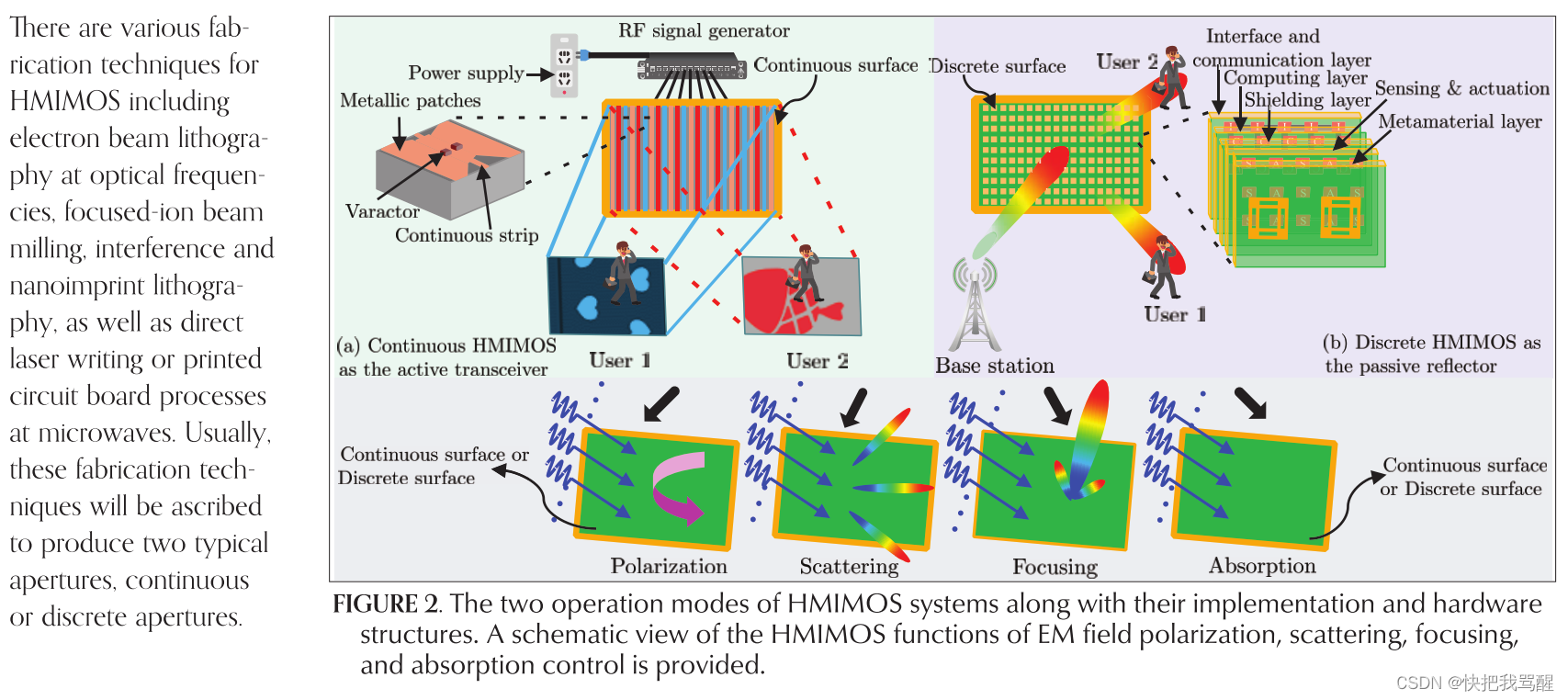
连续的 HMIMOS：连续的 HMIMOS 将几乎不可数的无限数量的元件集成到有限的表面积中，以形成空间上连续的收发器孔径 [13, 14]。为了更好地理解连续表面的操作及其通信模型，我们首先简要描述光学全息概念的物理操作。全息术是一种基于电磁波的干涉原理来记录电磁场的技术，电磁场通常是信号源从物体上散射的结果。然后，记录的电磁场可用于根据衍射原理重建初始场。应该指出的是，连续孔径上的无线通信受到光学全息术的启发，如图 1 所示。在训练阶段，从 RF 源生成的训练信号通过分束器分成两个波，物体和参考波。物体波被引导到物体，一些反射波与未撞击物体的参考波束混合在一起，被馈送到 HMIMOS。在通信阶段，传输的信号通过 HMIMOS 的空间连续孔径转换为目标用户所需的波束。由于连续孔径受益于理论上无限数量的天线的集成（可以被视为大规模 MIMO 的渐近极限），因此其潜在优势包括实现更高的空间分辨率，并能够创建和检测任意空间频率分量的电磁波，并且没有不需要的旁瓣。

离散的HMIMOS： 分立的 HMIMOS 通常由许多由低功耗软件可调超材料制成的分立单元组成。以电子方式修改单元电池的电磁特性的方法包括从现成的电子元件到使用液晶、微机电系统甚至机电开关和其他可重新配置的超材料。这种结构与传统的MIMO天线阵列有很大不同。离散表面的一个实施例基于具有电子可操纵反射特性的离散“元原子”[6]。如前所述，另一种类型的离散表面是基于光子天线阵列的有源表面。与连续的HMIMOS相比，分立的HMIMOS从实现和硬件的角度来看有一些本质的区别，下文将对此进行介绍。

制造方法

HMIMOS 有多种制造技术，包括光频电子束光刻、聚焦离子束铣削、干涉和纳米压印光刻，以及微波直接激光写入或印刷电路板工艺。通常，这些制造技术将归因于产生两种典型的孔径，连续的或离散的孔径，如图2所示。图2a描述了利用可编程超材料近似实现连续微波孔径的制造方法[13, 14] 。这种超粒子结构采用变容二极管加载技术来拓宽其频率响应范围，并实现连续孔径和可控反射相位。它是一种连续的单层金属结构，由大量的超粒子组成。每个超粒子包含两个金属梯形贴片、一个中央连续条和变容二极管。通过独立、连续地控制变容二极管的偏置电压，可以对连续 HMIMOS 的表面阻抗进行动态编程，从而在较宽的频带范围内控制反射相位、幅度状态和相位分布 [1]。应该强调的是，该阻抗图案是全息图的图，可以直接根据提供的参考波和反射物体波的场分布来计算，如图 1 所示。利用智能控制算法，波束形成可以利用全息原理来实现。

与连续孔径相比，HMIMOS 的另一个实例是基于离散孔径的实现，通常使用软件定义的超表面天线来实现。文献[6]提出了一种通用的逻辑结构（无论其物理特性如何），如图2b所示。其一般晶胞结构包含超材料层、传感和驱动层、屏蔽层、计算层以及具有不同目标的接口和通信层。具体来说，超材料层由石墨烯材料实现，用于通过可重构模式提供所需的电磁行为，而传感和驱动层的目标是修改超材料层的行为。屏蔽层由简单的金属层制成，用于解耦顶层和底层的电磁行为，以避免相互干扰。计算层用于执行来自接口层或传感器的外部命令。最后，接口和通信层旨在协调计算层的动作并通过可重新配置接口更新其他外部无线实体。

虽然 HMIMOS 的开发还处于起步阶段，但不同类型的该技术的基本原型制作工作已经可用。初创公司Greenerwave开发了分立式HMIMOS，这展示了使用分立式超表面天线的HMIMOS概念的基本可行性和有效性。相比之下，另一家初创公司Pivotalcommware在比尔盖茨资本的投资下，正在开发基于低成本连续超表面的连续HMIMOS的初始商业产品，这进一步验证了HMIMOS概念的可行性以及全息技术的进步。非常需要持续的原型开发，以通过全新的全息波束形成技术来证明 HMIMOS 概念，并发现迫切需要研究的潜在新问题。

---

工作模式

通常考虑 HMIMOS 的以下四种操作模式： 连续 HMIMOS 作为活动收发器 （Continuous HMIMOS as Active Transceivers）；分立的 HMIMOS 作为无源反射器（Discrete HMIMOS as Passive Reflectors）；分立的 HMIMOS 作为有源收发器；以及连续的 HMIMOS 作为无源反射器。考虑到最近的研究兴趣和篇幅限制，我们详细阐述了前两种代表性的操作模式，如图2所示。

✅ Continuous HMIMOS as Active Transceivers：根据此操作模式，连续 HMIMOS 用作有源收发器。射频信号在其背面生成，并通过可操纵的分配网络传播到由大量软件定义和电子可操纵元件构成的连续表面，这些元件向目标用户生成多个波束。主动连续HMIMOS和被动可重构HMIMOS的显着区别在于，前者的波束赋形过程是基于全息概念完成的，全息概念是一种基于软件定义天线的新型动态波束赋形技术，具有成本低、重量轻、尺寸紧凑、低功耗硬件架构等特点。

✅ Discrete HMIMOS as Passive Reflectors：HMIMOS 的另一种操作模式是镜子或“波收集器”，其中 HMIMOS 被认为是离散和无源的。在这种情况下，HMIMOS 构成了可重新配置的单位单元，如前所述，这使得它们的波束形成模式类似于传统的波束形成[10]，这与连续收发器 HMIMOS 系统不同。值得注意的是，大多数现有工作（例如[5,7,8]）都集中在这种更易于实现和分析的HMIMOS操作模式上。

[5] C. Huang et al., “Reconfi gurable Intelligent Surfaces for Ener-
gy Effi ciency in Wireless Communication,” IEEE Trans. Wire-
less Commun., vol. 18, no. 8, Aug. 2019, pp. 4157–70.

[7] N. Kaina et al., “Shaping Complex Microwave Fields in
Reverberating Media with Binary Tunable Metasurfaces,”
Sci. Rep. 4, No. 076401, 2014, pp. 1–7.

[8] Q. Wu and R. Zhang, “Intelligent Reflecting Surface
Enhanced Wireless Network via Joint Active and Passive
Beamforming,” IEEE Trans. Wireless Commun., vol. 18, no.
11, Nov. 2019, pp. 5394–5409.

Functionality, Characteristics, and Communication Applications

HMIMOS 系统的不同制造方法导致了各种功能和特性，其中大多数与未来 6G 无线系统的期望（例如 Tb/s 峰值速率）非常相关。在本节中，我们将重点介绍 HMIMOS 的功能和主要特性，并讨论其多样化的无线通信应用。

函数类型

智能表面可以支持广泛的电磁交互，下文中称为功能。由于其可编程特性，并根据它们是通过离散元件还是连续元件的结构实现，HMIMOS 有四种常见的功能类型，如图 2 底部所示：

• F1：电磁场极化，是指波的电场和磁场的振荡方向的可重构设置。
• F2：电磁场散射，其中表面将具有给定到达方向的撞击波重定向至所需方向或多个并发所需方向。
• F3：铅笔式聚焦，当 HMIMOS 充当透镜将电磁波聚焦到近场或远场中的给定点时发生。准直（即反向功能）也属于这种波束形成操作的一般模式。
• F4：电磁场吸收，实现传入电磁场的最小反射和/或折射功率。

---

---

---

这篇文章貌似没有具体讲数学建模细节，所以看下一篇

---

---

---

---

Multi-User Holographic MIMO Surfaces: Channel Modeling and Spectral Efficiency Analysis

https://ieeexplore.ieee.org/abstract/document/9779586

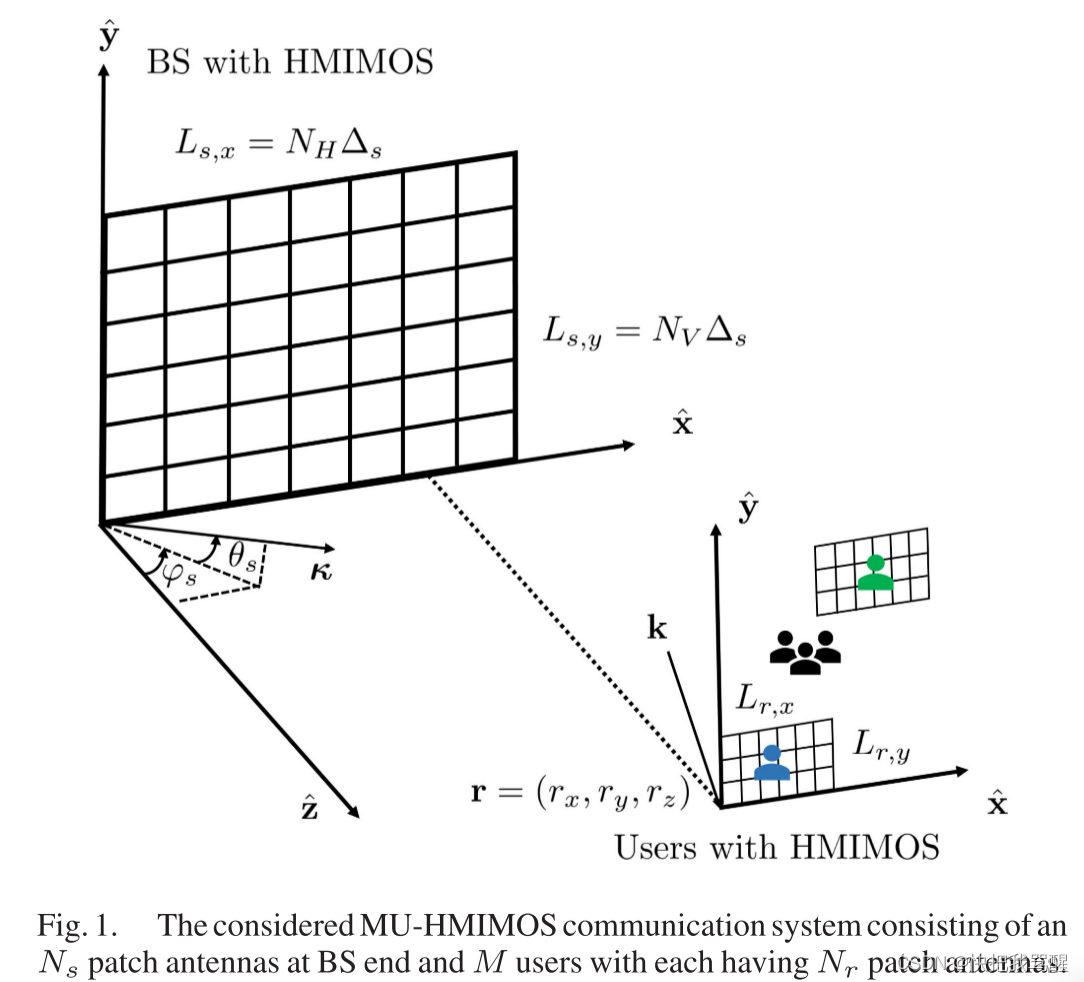
多用户全息多输入多输出表面（MU-HMIMOS）范式能够以最小的功耗实现大的连续孔径，最近被认为是未来无线网络的节能解决方案，提供了更高的性能。根据所需的通信、定位和传感目标，灵活地影响电磁 (EM) 波传播。 MU-HMIMOS 无线系统中易于处理的信道建模是最关键的研究挑战之一，这主要是由于过多的紧密间隔的贴片天线引起的耦合效应。在本文中，我们重点关注多用户 MIMO 通信下行链路的这一挑战，并将符合 EM 的信道模型扩展到多用户情况，该模型使用傅里叶平面波近似在波数域中表示。基于所提出的信道模型，我们研究了最大比率传输和迫零（ZF）预编码方案的频谱效率。我们还引入了一种新颖的硬件高效 ZF 预编码器，利用诺伊曼级数 (NS) 展开来取代所需的矩阵求逆运算，由于设想的 MU 中存在大量贴片天线，因此很难以传统方式计算矩阵求逆运算。 HMIMOS 通信系统。与忽略天线耦合效应的传统独立且相同的瑞利衰落信道相比，所提出的符合EM的信道模型捕获了由非常小的天线间距引起的互耦合。我们广泛的性能评估结果表明，即使对于高度相关的情况，我们的理论性能表达式也足够好地接近所考虑的线性预编码方案的模拟可实现的频谱效率，从而验证了所提出的分析框架的有效性和鲁棒性。此外，经验证，所提出的基于 NS 的 ZF 预编码器可实现与传统 ZF 相似的性能，同时需要较低的硬件复杂性，从而为 MU-HMIMOS 通信系统的实际设计提供硬件有效的解决方案。

introduction

符合 EM 的信道建模

在本节中，我们针对远场电磁波传播的情况，利用近似傅立叶平面波级数展开，并为多用户 HMIMOS 通信系统提出符合电磁兼容的远场信道模型。

额，貌似这篇文章主要关注的是反射全息MIMO和接收全息MIMO，而不是我之前想要的反射面。

---

---

---

---

Terahertz Massive MIMO With Holographic Reconfigurable Intelligent Surfaces论文笔记

摘要

我们提出了一个全息版本的可重构智能表面（RIS）和太赫兹（THz）大规模多输入多输出系统的应用程序。利用THz电子元件的小型化，RISs可以通过密集地封装亚波长单位单元来实现，以便实现连续或准连续的孔径并实现全息通信。在本文中，特别是，我们推导出全息RIS的波束图案。我们的分析表明，一个理想的全息RIS的波束模式可以很好地被超密集RIS近似，它具有更实用的硬件架构。此外，我们提出了一个闭环信道估计（CE）计划，以有效地估计宽带信道的特点太赫兹大规模MIMO系统的全息RISs的帮助。所提出的CE方案包括下行链路粗CE阶段和上行链路细粒度CE阶段。明智地设计上行链路导频信号以获得良好的CE性能。此外，为了减少导频开销，我们引入了一种基于压缩感知的CE算法，该算法利用了太赫兹MIMO信道在角度域和延迟域的双重稀疏性。仿真结果表明了全息RISs的优越性，非全息的，所提出的CE方案的有效性。

introduction

在过去的几年中，由于移动的设备和多媒体应用的爆炸性增长，对无线数据流量的需求显著增加[1]，[2]。为了满足这些需求，太赫兹（THz）波段的可能使用引起了工业界和学术界的极大兴趣[1]-[7]。与毫米波（mmWave）频带相比，THz频带可以提供更丰富的带宽（从0.1THz到10 THz）、更高的数据速率（从几十Gbps到几Tbps）和更低的延迟（微秒量级[1]）。THz频段被认为是实现beyond 5G和6 G通信的有希望的候选者。

尽管THz频带具有吸引人的优点，但在THz频率下建立可靠的传输链路是一项重要的任务。这是因为（i）太赫兹波段存在强烈的大气衰减和极高的自由空间损耗;以及（ii）视线（LoS）链路对THz频带中的阻塞效应非常敏感，因此链路通常是间歇的。这些缺点可能负面地影响通信范围，并且可能严重地降低THz通信系统的服务覆盖。在THz通信的上下文中部署大规模[4]或甚至超大规模[5]多输入多输出（MIMO）系统可以提供相当大的波束成形增益以便克服所提到的限制，但是它可能导致负担不起的功耗并且可能给整个通信系统设计带来过重的负担。

最近，新兴的可重构智能表面（RIS）技术已经被提出并应用于无线通信，以增强各种场景中的通信性能，例如MIMO通信、物理层安全、无人机通信、同时无线信息和功率传输、认知无线电系统[8]-[33]。RIS由无源和基于超材料的可重构元件制成，可以操纵入射电磁（EM）信号的相位和振幅，以便将它们反射到期望的方向。更重要的是，与其他传输技术（如有源中继[16]）不同，RIS不需要耗电的射频链（RFC）和功率放大器，这可能有利于开发绿色和经济高效的通信。尽管最近已经研究了RIS在毫米波波段的应用[28]-[31]，但是RIS在THz通信中的应用仍处于起步阶段。

先前工作

近年来，基于RIS-MIMO技术的通信技术引起了人们的广泛关注。[20]的作者提出了一种基于凸优化的联合有源和无源波束成形方案，以最大化接收器处的信号与干扰加噪声比（SINR）。在[21]中考虑了类似的场景，其中经由投影梯度上升算法来计算使SINR最大化的RIS的相位。在[22]中，高级深度强化学习（DRL）方法被认为是用于RIS辅助多用户系统中的波束成形设计。[23]的作者为大型RIS开发了一个可扩展的优化框架，基于该框架，提出了一种两阶段方法，包括离线设计和在线优化，以优化RIS。在[24]中研究了RIS的反射元件的实际振幅和相移模型，其中通过考虑每个反射元件的相位相关振幅变化来进行波束形成优化。在[25]中，作者介绍了一种新的RIS通信模型，该模型考虑了RIS散射元件的振幅和相位响应之间的相互耦合和相互作用。

[20]-[25]中的设计依赖于全局信道状态信息（CSI）的知识。由于在RISs中不使用有源元件，因此信道估计（CE）是具有挑战性的任务，并且是RIS-aided MIMO系统中的必要先决条件。在[26]和[27]中，作者提出了一种基于最小二乘（LS）估计器的用于RIS辅助系统的CE算法，分别应用于频率平坦衰落信道和频率选择性衰落信道。为了在部署大尺寸阵列时进一步促进CE任务，在[28]、[29]中研究了基于压缩感测（CS）的CE方案，其中利用角度域中的毫米波信道的固有稀疏性以便减少导频开销。在[30]和[31]中，提出了一种应用于毫米波频带的RIS的新架构，其中在RIS处有几个有源RFC可用，以便真实的学习信道。基于该架构，深度学习（DL）技术被用于CE和波束成形。

就RIS在THz通信中的应用而言，[32]的作者提出了一种用于室内应用的RIS辅助THz MIMO通信系统。在[32]中基于CS和DL技术两者提出了联合CE和数据速率最大化方案。在[33]中，研究了THz波段中的RIS辅助安全传输问题。最大化保密率的相位移在RIS的基础上得到凸优化。基于目前的研究状况，我们表明，设计的RIS辅助太赫兹通信系统仍处于早期发展阶段。

最近，全息通信的概念被提出作为 MIMO [34]-[36] 和 RIS 辅助 [37] 通信的新范式转变。全息通信的主要特征之一是将大量微型且廉价的天线或可重构元件集成到紧凑的空间中，以实现具有空间连续孔径的全息阵列[34]-[37]。由于太赫兹电子元件的小型化，这种全息架构在太赫兹频段更容易实现。例如，在[32]中，每个石墨烯基反射元件的尺寸为200μm×190μm，载波频率为0.22THz，对应于波长λ≈1360μm。因此，反射元件的间隔可以比λ/2更密集，从而形成空间连续的表面[37]，因为所得表面是可均匀化的[8]。这种密集或连续的 RIS 实施方式被称为全息 RIS。 [34]和[37]分别研究了基于主动全息表面的通道建模和数据传输方案。然而，据我们所知，目前还没有研究工作解决无源全息通信的物理层传输设计，其中部署了具有空间连续孔径的近无源全息RIS。

论文贡献

在这项工作中，我们把我们的注意力集中在太赫兹波段的大规模MIMO系统中的全息RISs的应用的分析。特别是，本文的主要贡献可以总结如下：

1. 我们推导出的离散元素的RIS的波束方向图，并提出了一个角域波束形成框架。通过对RIS元素的反射系数的傅里叶分析，我们证明了有离散元素的RIS的波束模式可以表示为Dirichlet核函数的加权积分。在此基础上，我们提出了一个角度域波束形成框架。设计波束图中的加权因子，并通过对所获得的加权因子进行傅里叶变换来重构RIS的相应反射系数。
2. **我们将分析和设计推广到（连续）全息RISs。**基于所提出的波束成形框架，我们推导并获得了两种重要情况下的波束成形设计的封闭形式的解决方案，即，窄波束控制（NBS）和空间带通滤波（SBF），它们在RIS辅助通信系统中起着重要作用。我们进一步扩展这些解决方案的全息RISs，其中的元素是紧密间隔，以便产生一个几乎连续的空间孔径。结果表明，一个理想的全息RIS的波束模式可以很好地被近似为超密集RIS，它具有实用的硬件架构。
3. 我们提出了一个闭环CE计划，基于全息RIS，有效地估计太赫兹大规模MIMO系统的宽带信道。所提出的方法包括下行链路和上行链路传输。在下行链路传输中，全息RIS使用SBF波束成形，使得用户可以粗略地估计LoS角度的范围。在随后的上行链路传输中，具有相似LoS角度的用户被调度到同一组中，并且利用粗略估计的LoS角度来设计用于更细粒度的上行链路CE的上行链路导频信号。为了进一步减少上行链路导频开销，引入了基于CS的CE方案，其中利用了THz MIMO信道在角度域和延迟域两者中的双重稀疏性。

SYSTEM DESCRIPTION AND CHANNEL MODEL

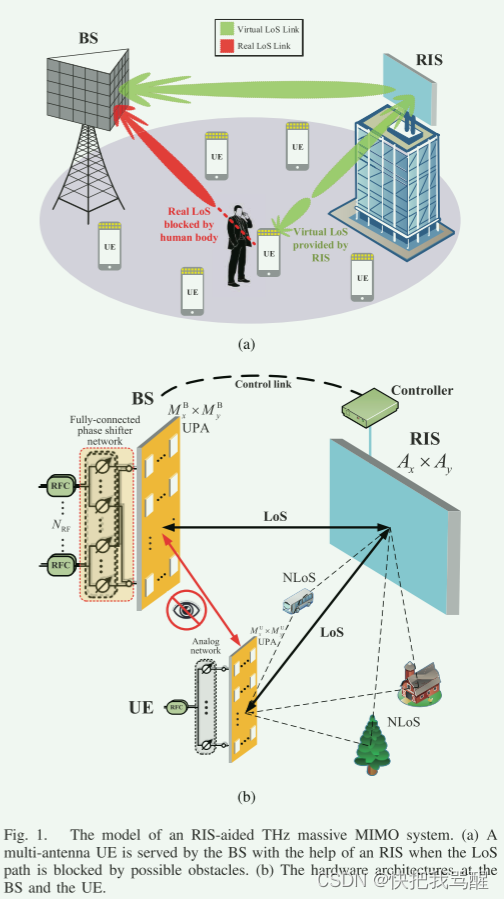
在这一节中，我们提出了系统模型和有效的基带信道模型的考虑RIS aided太赫兹大规模MIMO系统在频率选择性衰落信道。我们考虑一个RIS辅助的THz大规模MIMO系统，该系统工作在时分双工（TDD）模式，如图1所示。基站（BS）和用户设备（UE）分别采用由$M^{\mathrm{B}}=M_x^{\mathrm{B}}\times M_y^{\mathrm{B}}$和$M^{\mathrm{U}}=M_x^{\mathrm{U}}\times M_y^{\mathrm{U}}$天线组成的半波长间隔均匀平面阵列（UPA），其中$M_x^{\mathrm{B}}$ （$M_x^{\mathrm{U}}$）和$M_y^{\mathrm{B}}$ （$M_y^{\mathrm{U}}$）分别是沿着方位和仰角方向的天线数。部署物理大小为$A_x\times A_y$ 的RIS以增强BS的有效覆盖。低功率RIS控制器连接到RIS，并且由BS通过控制链路操作。BS执行波束成形优化并通过控制链路将结果馈送到RIS控制器，使得可以相应地调整RIS的每个反射元件的反射系数。如图在图1（a）中，我们假设BS与UE之间的LoS链路被障碍物或人体阻挡。因此，UE仅经由RIS与BS通信，这被认为是RIS辅助系统中的虚拟LoS传输[29]。为了降低功耗和硬件成本，在BS处考虑混合模拟-数字架构，即，在BS处仅存在$N_{RF}\ll M^B$个RFC，并且它们中的每一个通过$M^B$个移相器连接到$M^B$个天线。此外，每个UE采用模拟波束成形，其中仅一个RFC通过$M^U$个移相器连接到$M^U$个天线。采用具有$K$个子载波和采样周期$T_s$的正交频分复用（OFDM）传输方案。在每个OFDM符号之前添加长度为$N_{CP}{T}_S$的循环前缀（CP）以避免符号间干扰。中心载波频率是对应于波长$\lambda$的$f_c$。

---

---

---

Holographic MIMO for LEO Satellite Communications Aided by Reconfigurable Holographic Surfaces

超密集低地球轨道（LEO）卫星通信网络具有提供高速数据服务的巨大潜力。为了补偿卫星通信中严重的路径损耗，一个关键的概念使能器是具有空间连续孔径的全息多输入多输出（HMIMO），其可以以小的天线尺寸实现高的定向增益。在本文中，我们考虑了一种新型的超材料天线，称为可重构全息表面（RHS）与用户终端（UT）集成，以支持LEO卫星通信**。RHS由密集封装的亚波长超材料元件组成，可以实现连续或准连续的孔径，并为实现HMIMO提供了一种实用的方法。为了获得所需的波束方向的卫星，我们提出了一个LEO卫星跟踪方案的时间变化规律的基础上，这样就可以避免频繁的卫星定位。全息波束形成算法的和速率最大化，然后开发的封闭形式的最佳全息波束形成器。证明了算法对卫星位置跟踪误差的鲁棒性。仿真结果验证了理论分析的正确性，并表明当RHS阵元间距较小，阵元数目较多时，RHS阵元的和速率优于相同物理尺寸的传统相控阵。此外，与相控阵相比，RHS还为追求高数据速率提供了更具成本效益的解决方案。
low-Earth-orbit (LEO) 低地球轨道
Reconfigurable Holographic Surfaces RHS 可重构全系表面
user terminals (UTs) 用户终端
在本节中，我们介绍了一种RHS辅助的LEO卫星通信系统，其中配备有RHS的一个UT向多个LEO卫星发送。在此基础上，给出了全息波束形成模型。

通过利用全息原理，RHS可以实现动态波束形成，以克服卫星的移动性，而不依赖于复杂的相移电路和笨重的机械。

系统模型

在本节中，我们介绍了一种RHS辅助的LEO卫星通信系统，其中配备有RHS的一个UT向多个LEO卫星发送。在此基础上，给出了全息波束形成模型。

场景描述：

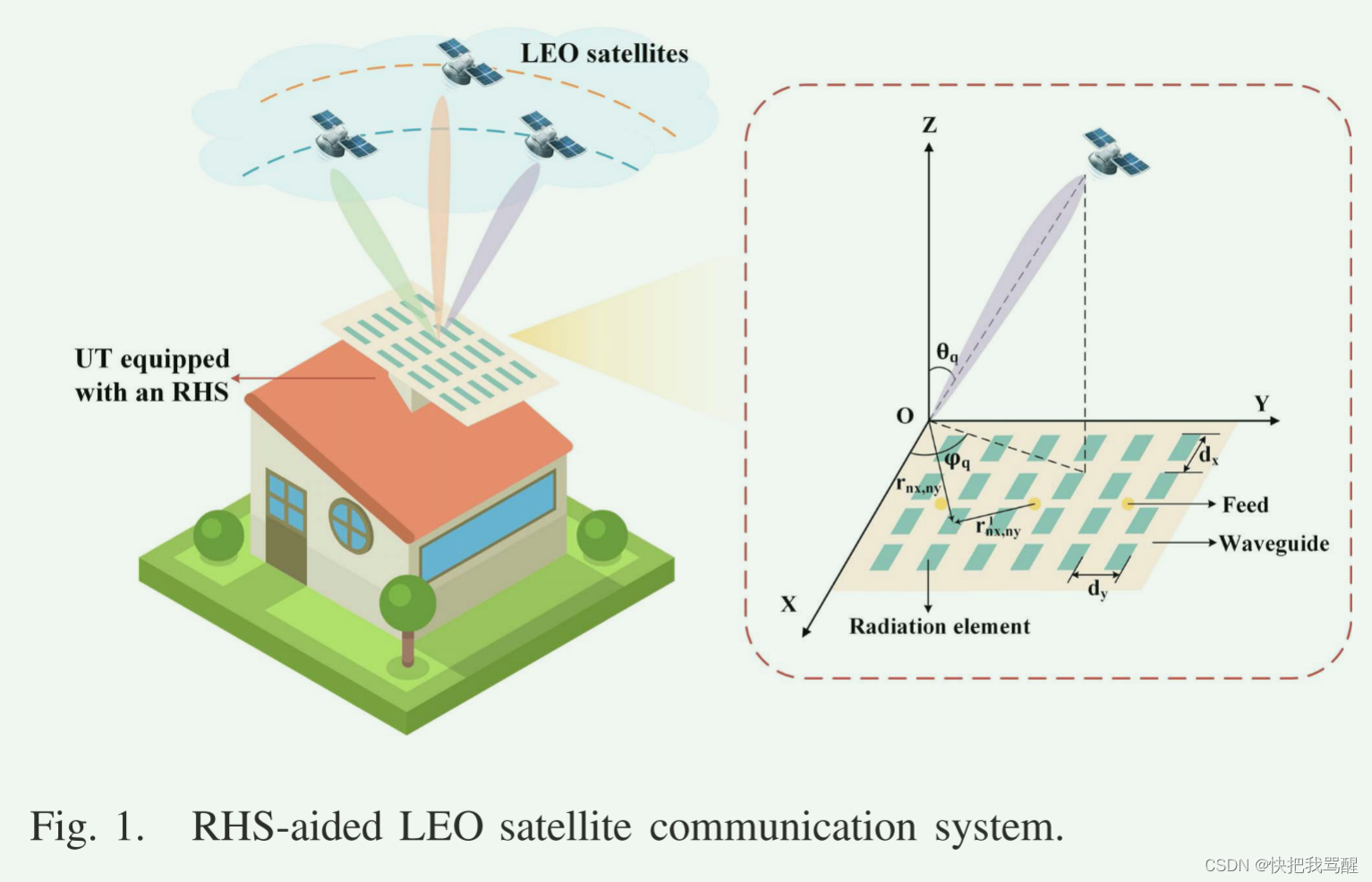
如图在图1中，我们考虑上行链路RHS辅助的LEO卫星通信系统，其中配备有RHS的UT在Ka频带频谱上将数据流上传到由$Q=1,...,q,...,Q$表示的$Q$个LEO卫星，以用于卫星回程网络接入。不失一般性，假设每个LEO卫星配备有K个天线。通过利用全息原理，RHS可以实现动态波束形成，以克服卫星的移动性，而不依赖于复杂的相移电路和笨重的机械。

RHS是主要由三部分组成的漏波天线，即，$L$个馈源、一个波导和$N$个亚波长超材料辐射元件。馈源嵌入在RHS的底层中，并产生入射电磁波，其也被称为参考波，携带用于卫星的预期信号。参考波然后沿着波导传播。在传播过程中，参考波通过辐射元件将其能量辐射到自由空间中，并且辐射波也被称为漏波[10]，其中漏波的波形与发射信号的波形相同。RHS可以控制元件的电磁响应（诸如辐射振幅）以构建全息图案，该全息图案记录参考波和期望的物波之间的干涉。具体地，可以通过简单的基于二极管的幅度控制器[21]来控制每个辐射元件处的参考波的辐射幅度，以表示干涉的幅度。因此，来自每个辐射元件的泄漏波可以根据全息图案独立地成形。来自不同元件的泄漏波的叠加最终产生朝向卫星的物波。

Holographic Beamforming Model

在这一小节中，我们阐述了全息原理的RHS，在此基础上提出的全息波束形成矩阵。

Without loss of generality, as shown in Fig. 1, we adopt the Cartesian coordinate where the $x-y$ plane coincides with the RHS, and the $z$ -axis is vertical to the RHS. Denote the number of radiation elements along the $x$ -axis and $y$ -axis as $N_x$ and $N_y$ , respectively, satisfying $N=N_x\times N_y$ . Denote the inter-element spacing of the RHS along the $x$ -axis and $y$ -axis as $d_x$ and $d_y$ , respectively. The position vector of the $\left(n_x,n_y\right)$ -th element can then be given by ${\mathbf{r}}_{n_x,n_y}={\left[n_x{d}_x,n_y{d}_y,0\right]}^T$ , where n x = { 1 , 2 , ⋯ , N x } n_{x}=\left\{1,2, \cdots, N_{x}\right\} nx​={1,2,⋯,Nx​} and n y = { 1 , 2 , ⋯ , N y } n_{y}= \left\{1,2, \cdots, N_{y}\right\} ny​={1,2,⋯,Ny​} .

At the $\left(n_x,n_y\right)$ -th radiation element, the reference wave generated by feed $l$ and the wave propagating in free space with the desired direction of $(\theta ,\phi )$ can be given by [12]

$$\begin{array}{rl}{\Psi }_{ref}\left({\mathbf{r}}_{n_x,n_y}^l\right)& =\exp \left(-j{\mathbf{k}}_s\cdot {\mathbf{r}}_{n_x,n_y}^l\right)\\ {\Psi }_{obj}\left({\mathbf{r}}_{n_x,n_y},\theta ,\phi \right)& =\exp \left(-j{\mathbf{k}}_f\cdot {\mathbf{r}}_{n_x,n_y}\right)\end{array}\text{\hspace{1em}(1,2)}$$

where ${\mathbf{k}}_s$ is the propagation vector of the reference wave in the waveguide, ${\mathbf{r}}_{n_x,n_y}^l$ is the distance vector from the feed $l$ to the $\left(n_x,n_y\right)$ -th radiation element. The interference between the reference wave and the object wave is defined as
$${\Psi }_{intf}\left({\mathbf{r}}_{n_x,n_y}^l,\theta ,\phi \right)={\Psi }_{obj}\left({\mathbf{r}}_{n_x,n_y},\theta ,\phi \right){\Psi }_{ref}^{\ast }\left({\mathbf{r}}_{n_x,n_y}^l\right)\text{\hspace{1em}(3)}$$
When such interference is excited by the reference wave, the
generated wave satisfies
$${\Psi }_{intf}{\Psi }_{ref}\propto {\Psi }_{obj}{\left|{\Psi }_{ref}\right|}^2\text{\hspace{1em}(4)}$$
implying that it propagates in the desired direction of $(\theta ,\varphi )$.

因此，包含在${\Psi }_{intf}$中的信息，也称为全息图案，被认为是由辐射元件记录的。为此，RHS中的每个辐射元件控制参考波的辐射幅度，而不是传统的相位控制方法。振幅控制方法的主要思想是，其参考波与物体波同相的元件被调谐为强烈辐射（大辐射振幅），而异相的元件被失谐，以便不辐射（小辐射振幅）[21]。

注意，干扰的真实的部（$\text{Re}[{\Psi }_{intf}]$），即参考波与物波之间的相位差的余弦值随着相位差的增大而减小，这恰好满足上述幅度控制要求。因此，$\text{Re}[{\Psi }_{intf}]$可以表示每个元件处的参考波的辐射幅度。为了避免负值，$\text{Re}[{\Psi }_{intf}]$被归一化为$[0,1]$。然后，可以通过[16]在数学上参数化每个元件的辐射振幅以生成在方向$(\theta ,\varphi )$上传播的波。

$$m\left({\mathbf{r}}_{n_x,n_y}^l,\theta ,\phi \right)=\frac{\mathrm{Re}\left[{\Psi }_{intf}\left({\mathbf{r}}_{n_x,n_y}^l,\theta ,\phi \right)\right]+1}{2}\text{\hspace{1em}(5)}$$

根据（5），可以看出，一个全息图案对应于一个期望的波方向。考虑到对应于不同期望方向的不同全息图案的叠加，然后可以由RHS生成朝向卫星的多个定向波束。具体地，这种叠加的全息图案被计算为对应于每个物体光束的辐射振幅分布的加权和。因此，每个元件的归一化辐射幅度可以表示为
$$m_{n_x,n_y}=\sum _{q=1}^Q\sum _{l=1}^L{a}_{q,l}m\left({\mathbf{r}}_{n_x,n_y}^l,{\theta }_q,{\phi }_q\right)\text{\hspace{1em}(6)}$$

where $\left({\theta }_q,{\phi }_q\right)$ is the position of satellite $q$ , and $a_{q,l}$ is the amplitude ratio for the beam towards satellite $q$ from feed $l$ satisfying

$$\sum _{q=1}^Q\sum _{l=1}^L{a}_{q,l}=1\text{\hspace{1em}(7)}$$

This constraint is set to make the radiation amplitude of each element $m_{n_x,n_y}$ lie in $[0,1]$ to guarantee the power radiated from the element is no larger than the power accepted by the element. Specifically, we denote the power accepted by each element as $P_a$ , the efficiency of each element as $\eta$, which is defined as the ratio of the power accepted by each element to the total power $P_t$ of the reference waves from all feeds, i.e., $\eta =P_a/P_t$ . When the radiation amplitude of each element is $m_{n_x,n_y}$ , the radiated power of each element is $P_a\cdot m_{n_x,n_y}^2$ .

Note that the sum of the radiated power from each RHS element should be no larger than $P_t$, i.e., ${\sum }_{n_x=1}^{N_x}{\sum }_{n_y=1}^{N_y}\eta P_t\cdot m_{n_y,n_z}^2\le P_t$ , where $m_{n_x,n_y}$ varies with the desired beam directions. To guarantee the conservation of energy for each beam direction, we adopt the average value of $m_{n_x,n_y}^2$ , and thus, in the RHS, the efficiency of the element $\eta$ and the number of elements should satisfy ${}^3$

$$\sum _{n_x=1}^{N_x}\sum _{n_y=1}^{N_y}\eta P_t\cdot \mathbb{E}\left(m_{n_x,n_y}^2\right)\le P_t\Rightarrow \eta \cdot N_x{N}_y\le \frac{8}{3}\text{\hspace{1em}(8)}$$

由于RHS是漏波天线，因此漏波效应使得参考波的振幅随着其沿着波导传播而逐渐减小[22]。将参考波的传播过程中的泄漏常数表示为$\alpha$，则全息波束形成矩阵$\mathbf{M}\in {\mathbb{C}}^{N_x{N}_y\times L}$由以下元素形成
$$M_{n_x,n_y}^l=\sqrt{\eta }\cdot m_{n_x,n_y}\cdot e^{-\alpha \left|{\mathbf{r}}_{n_x,n_y}^l\right|}\cdot e^{-j{\mathbf{k}}_s\cdot {\mathbf{r}}_{n_x,n_y}^l}\text{\hspace{1em}(9)}$$

where $e^{-\alpha \left|{\mathbf{r}}_{n_x,n_y}^l\right|}$ and $e^{-j{\mathbf{k}}_s\cdot {\mathbf{r}}_{n_x,n_y}^l}$ denote the amplitude attenuation（幅度衰减） and the phase of the reference (参考波的相位) wave when it propagates to the $\left(n_x,n_y\right)$ -th element from feed $l$ , respectively.

RHS 辅助的 LEO 卫星通信方案

data transmission scheme

在本节中，我们概述了 RHS 辅助的多卫星通信方案，其中包括 LEO 卫星跟踪和数据传输。然后分别介绍了详细的数据传输方案和无需频繁卫星定位即可获得卫星位置的LEO卫星跟踪方案。

多星通信方案概述

由于LEO卫星的高机动性，卫星的位置随着轨道运动而变化，这会影响RHS和卫星之间的信道以及全息波束形成方案。为了支持UT和多颗LEO卫星之间的连续通信，我们开发了RHS辅助的多卫星通信方案。

共$Q$个LEO卫星

我们假设每颗LEO卫星绕地球的公转是匀速圆周运动，该假设在文献中被广泛使用，以使卫星通信的理论分析易于处理[23]，[24]。卫星 $q$ 的位置由其天顶角 ${\theta }_q$ 和方位角 ${\varphi }_q$ 表示。我们将通信时间划分为 $T$ 个时隙，用 $1,\dots ,t,\dots ,T$ 表示，长度为 $\Delta$，在每个时隙内，每颗卫星的位置 ${\theta }_q^{(t)},{\varphi }_q^{(t)}$被视为未改变。算法1总结了整个RHS辅助的多卫星通信方案。具体来说，在前两个时隙中，UT根据初始卫星定位确定数据传输方案（将在图2中说明）。在接下来的每个时段，UT根据卫星位置的时间变化规律[25]跟踪LEO卫星的位置，并相应地更新数据传输方案。

而且，低轨卫星还受到大气阻力、其他行星引力等各种扰动力的影响，造成相对漂移，跟踪误差会不断累积。为了解决这个问题，每颗LEO卫星将每隔$\tau$个时隙将接收信号强度（RSS）信息反馈给UT。如算法1所示，一旦RSS小于阈值${\rm Y}$ ，则重新获取卫星在接下来的两个时隙中的位置，并据此根据时间变化规律预测其在接下来的时隙中的位置。 LEO 卫星的位置。关于算法 1 的复杂性，我们观察到以下事实。在每个时隙中，UT根据命题1给出的时间变化规律来预测每个卫星$q$的位置，其复杂度为$\mathcal{O}(Q)$。因此，由于总共有$T$个时隙，算法1的复杂度为$\mathcal{O}(QT)$。下面我们将分别阐述数据传输方案和LEO卫星跟踪方案。

数据传输方案

傅里叶平面波模型

全系波束赋形问题公式化

我们的目标是通过优化全息波束形成方案 $\mathbf{M}$ 来最大化 RHS 辅助的 LEO 卫星通信系统在每个时隙的总速率，如下所示：
max ⁡ { M } ∑ q = 1 Q log ⁡ 2 ( 1 + Λ q K σ 2 [ ( F F H ) − 1 ] q , q ) , s.t.  ∑ q = 1 Q ∑ l = 1 L a q , l = 1. (22) \begin{array}{l} \max _{\{\mathbf{M}\}} \sum_{q=1}^{Q} \log _{2}\left(1+\frac{\Lambda_{q}}{K \sigma^{2}\left[\left(\mathbf{F F}^{H}\right)^{-1}\right]_{q, q}}\right), \\ \text { s.t. } \sum_{q=1}^{Q} \sum_{l=1}^{L} a_{q, l}=1 . \tag{22} \end{array} max{M}​∑q=1Q​log2​(1+Kσ2[(FFH)−1]q,q​Λq​​), s.t. ∑q=1Q​∑l=1L​aq,l​=1.​(22)

由于${\left[{\left({\mathbf{FF}}^H\right)}^{-1}\right]}_{q,q}$没有闭合形式的表达式，使得最优全息波束形成器的推导变得困难，我们考虑通过 把$R$ 变换为其上限$\hat{R}$来消除项 ${\left[{\left({\mathbf{FF}}^H\right)}^{-1}\right]}_{q,q}$ 。然后，我们重新表述总速率最大化问题以最大化 $\hat{R}$ 并导出最佳全息波束形成器。最后，我们将证明所导出的最优全息波束形成器正是原始和率最大化问题（22）的最优解。

---

---

---

Holographic MIMO Communications

来自Dr. Andrea Pizzo and Prof. Luca Sanguinetti的PPT

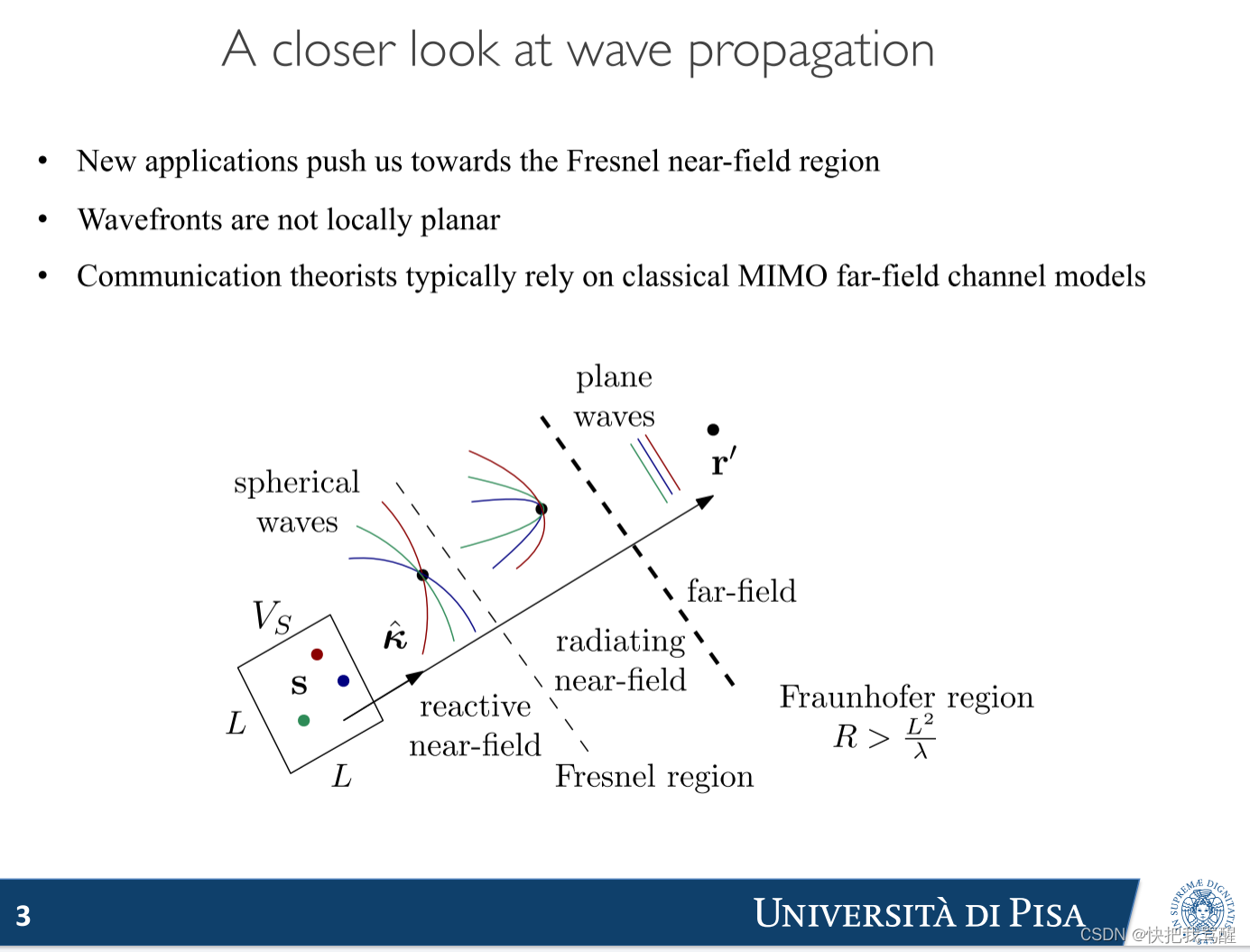
1. 数值电磁求解器对通信理论家没有用
2. i.i.d.瑞利衰落高估了可用的自由度（与天线成比例）
3. 随机场模型通常具有物理上无意义的相关性
4. 没有物理上可行的通道模型可供使用

Fourier plane-wave model!

1. 我们将波传播建模为线性时变系统
2. 固定信道在空间频率域中是低通带限的

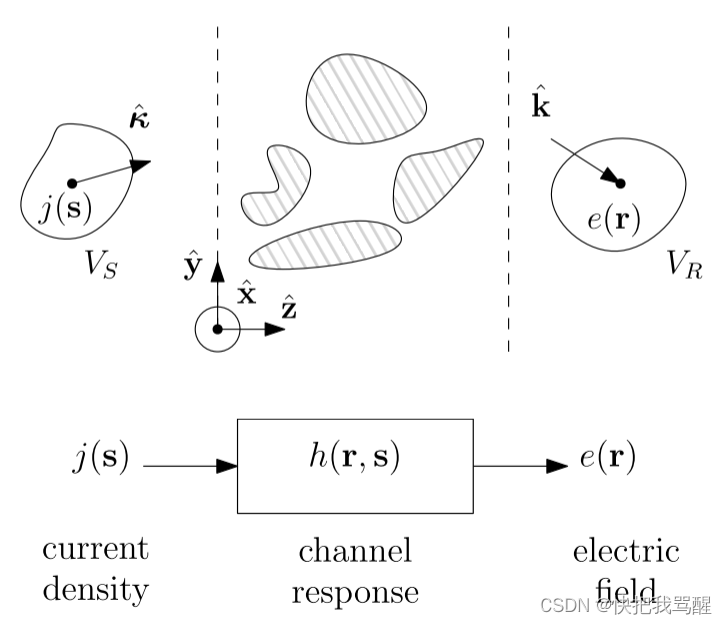
P6
傅里叶平面波级数展开

1. 信道响应可以分解为平面波
2. 在菲涅耳近场区域和任意散射中有效
3. 具有统计独立高斯系数的信道的正交描述

$$h(\mathbf{r},\mathbf{s})\approx \sum _{\left({\ell }_{\mathbf{x}},{\ell }_{\mathbf{y}}\right)\in {\mathcal{E}}_{\mathbf{r}}\left({\mathbf{m}}_{\mathbf{x}},{\mathbf{m}}_{\mathbf{y}}\right)\in {\mathcal{E}}_{\mathbf{s}}}{\mathbf{a}}_{\mathbf{r}}\left({\ell }_{\mathbf{x}},{\ell }_{\mathbf{y}},\mathbf{r}\right){\mathbf{H}}_{\mathbf{a}}\left({\ell }_{\mathbf{x}},{\ell }_{\mathbf{y}},{\mathbf{m}}_{\mathbf{x}},{\mathbf{m}}_{\mathbf{y}}\right){\mathbf{a}}_{\mathbf{s}}\left({\mathbf{m}}_{\mathbf{x}},{\mathbf{m}}_{\mathbf{y}},\mathbf{s}\right)$$

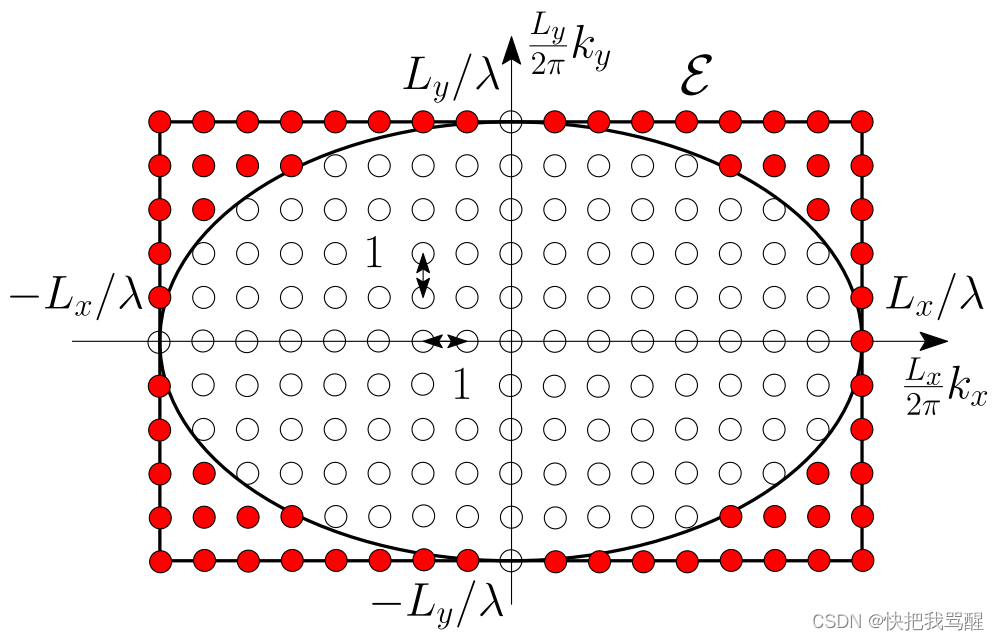
P7
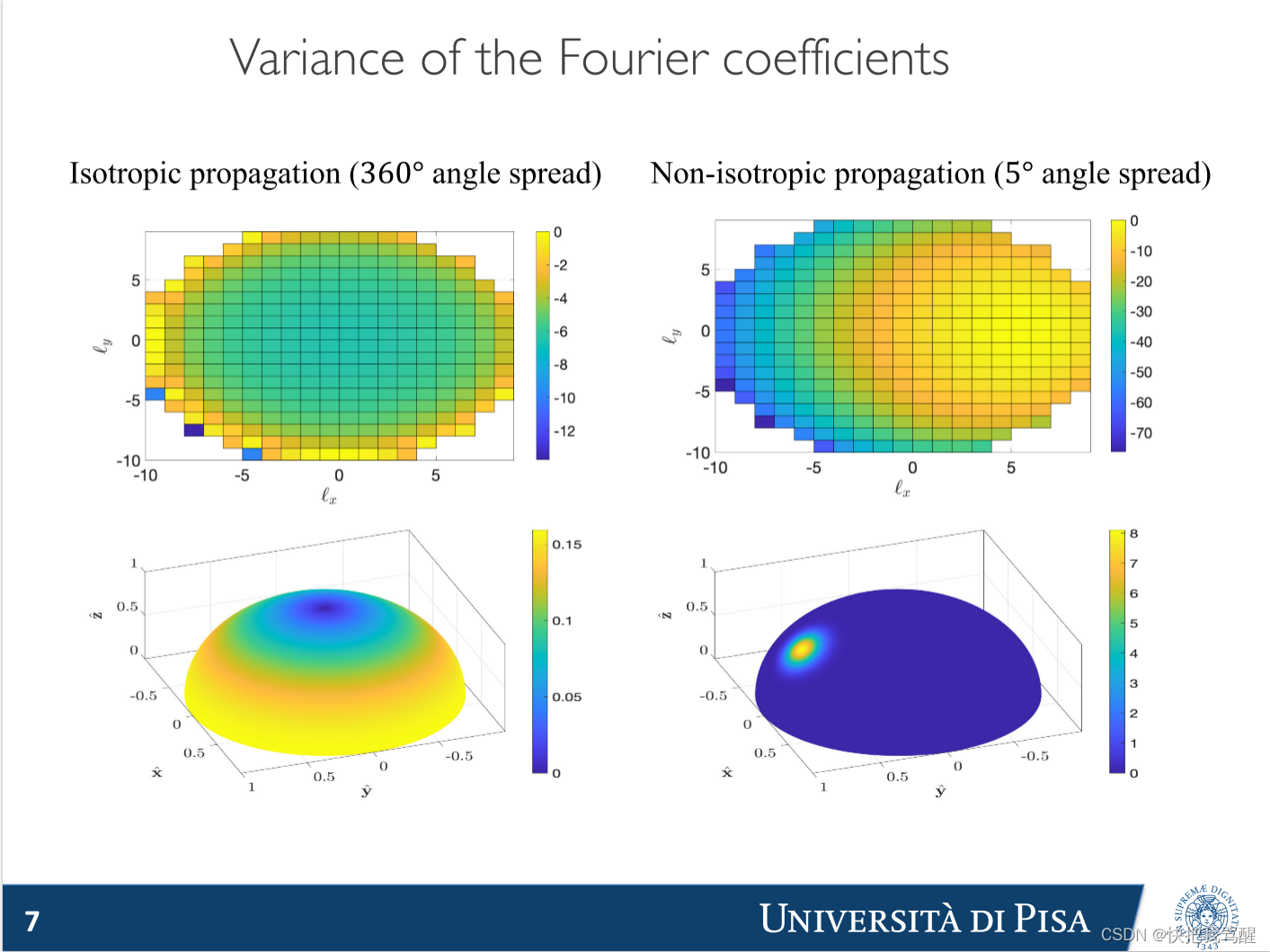
傅里叶系数的方差
各向同性传播（360° 角度扩展）
非各向同性传播（5° 角展）

P8

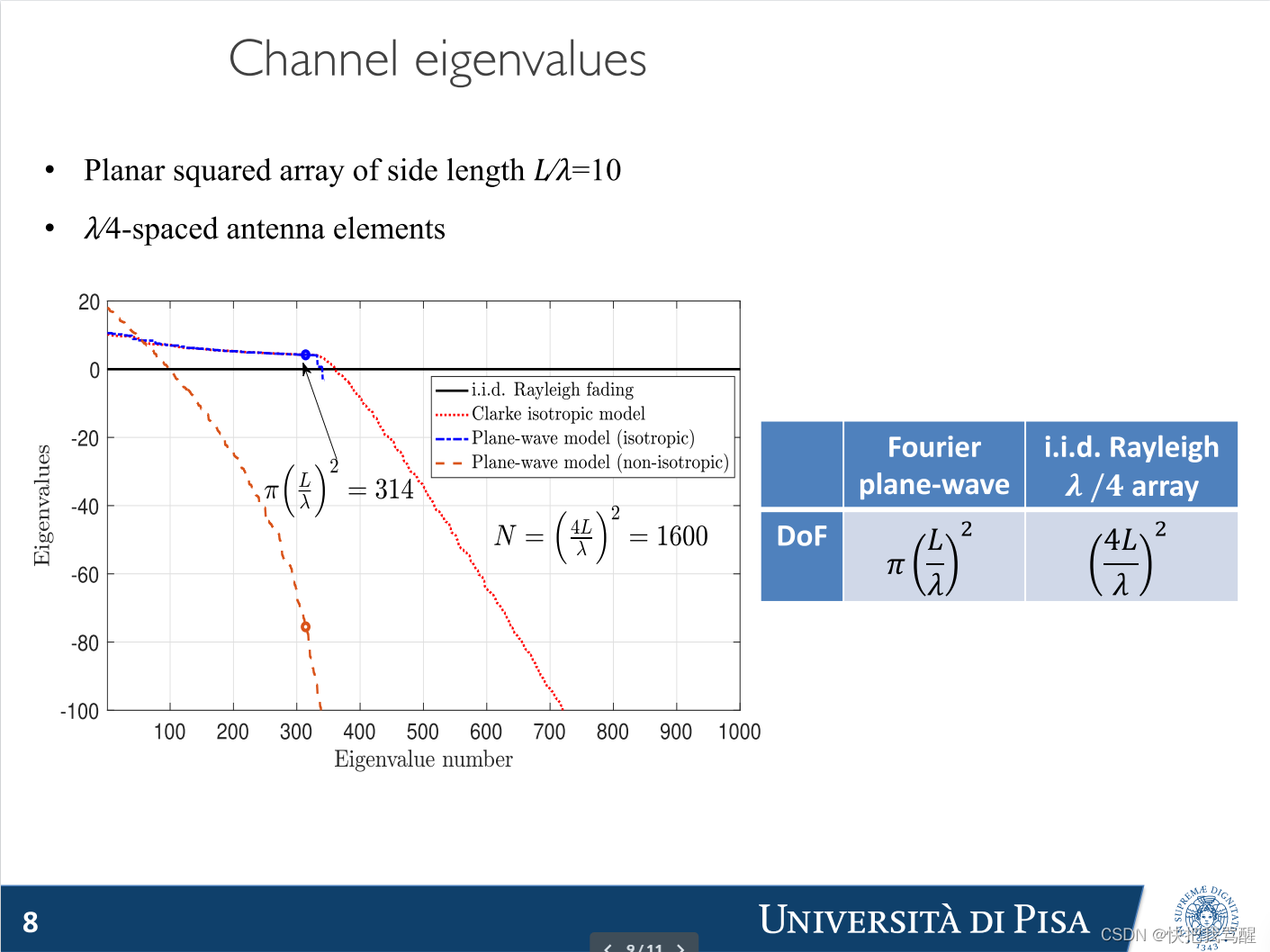
边长𝐿⁄𝜆=10 的平面方阵
𝜆/4-spaced antenna elements

---

问chatgpt如何计算信道的自由度？

信道的自由度是一个描述信道容量（通信信道传输信息的能力）的重要概念，通常用于衡量信道的带宽利用率和信息传输速率。信道的自由度与信号传输的特性有关，不同类型的信道具有不同数量的自由度。以下是一些常见信道的自由度计算方法的示例：

1. 添加白噪声高斯信道（AWGN）：
   对于一个单一的AWGN信道，其自由度通常与信道的带宽（B）和信噪比（SNR）有关。自由度（C）可以使用香农公式计算：

   C = B * log2(1 + SNR)

   其中，C表示信道的自由度，B表示信道的带宽，SNR表示信噪比。

2. 多天线信道（MIMO）：
   多输入多输出（MIMO）信道具有多个天线，其自由度的计算涉及到发射天线和接收天线的数量，以及信道特征矩阵的秩。对于一个MIMO信道，其自由度（C）可以计算为：

   C = min(M, N)

   其中，M表示发射天线数量，N表示接收天线数量。这个计算是一个简化的方法，通常用于理论分析。

3. 时分复用多路复用（TDMA）：
   对于时分复用多路复用（TDMA）系统，自由度的计算与时间槽的数量和分配给每个用户的时间槽数量有关。如果有N个时间槽，每个用户分配M个时间槽，那么信道的自由度可以计算为：

   C = N / M

   这表示每个用户在一段时间内可以传输的信息的数量。

4. 正交频分复用（OFDM）：
   正交频分复用（OFDM）系统的自由度与子载波数量和调制阶数有关。通常，OFDM信道的自由度可以计算为：

   C = N_subcarriers * log2(M)

   其中，N_subcarriers表示子载波的数量，M表示每个子载波的调制阶数。

请注意，以上计算方法是一些基本的示例，实际应用中可能会涉及更复杂的信道模型和调制方案。信道的自由度计算通常用于优化通信系统的设计，以实现更高的信息传输速率和更好的带宽利用率。

---

实际实施：

1. 信道响应的封闭形式、数学上可处理的 SVD
2. 在近场和远场以及任意散射下均有效
3. 可用自由度不随天线数量变化
4. 3D（体积）阵列不提供比两个平面阵列额外的自由度
5. 角度域统一等价于空间域但冗余较少
6. FFT 复杂性数据处理算法和信道估计

Reconfigurable Holographic Surface: Holographic Beamforming for Metasurface-Aided Wireless Communications

https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9431753

未来的第六代（6G）无线通信期望构建一个泛在的高数据速率智能信息网络。为了实现这种具有挑战性的愿景，可重构全息表面（RHS）因其具有低功耗和低硬件成本的精确多光束转向能力而被开发为一种有前途的解决方案。与传统的相控天线不同，RHS可以利用全息技术来控制在超表面上传播的参考波的辐射幅度。然后可以生成所需的目标波，无需复杂的相移电路，从而可以方便地实现收发器。这种幅度控制的全息波束形成引发了新的挑战，因为需要开发一种新的波束形成方案来处理受到非常规实域幅度约束的复杂域优化问题，这使得来自不同天线单元的辐射波的叠加变得困难。处理。在这封信中，我们考虑了一个 RHS 辅助的多用户通信系统，其基站配备了 RHS。我们提出了一个和速率最大化问题，并设计了一种新颖的幅度控制算法来解决该问题。仿真结果验证了所提方案的有效性。

简介

为了实现无处不在的智能信息网络，即将到来的第六代（6G）无线通信对天线技术如容量增强和低功耗硬件组件提出了严格的要求[1]。在现有的天线技术中，全息天线作为一种小尺寸、低功耗的平面天线，因其具有多波束控制能力、制造成本和硬件成本低而受到越来越多的关注。具体来说，全息天线利用元贴片在表面构建全息图案，（该全息图案）根据干涉原理记录参考波与期望目标波之间的干涉。然后可以通过全息图案改变参考波的辐射特性以生成期望的辐射图案。Specifically, the holographic antenna utilizes meta
patches to construct the holographic pattern on the surface, which
records the interference between the reference wave and the desired
object wave based on the interference principle. The radiation charac-
teristics of the reference wave can then be changed by the holographic
pattern to generate the desired radiation pattern.

然而，指数级增长的移动设备对传统的全息天线提出了巨大的挑战，因为一旦构建全息图案，其辐射图案就固定了。幸运的是，新兴的可重构全息表面（RHS）由于超材料的可控性而显示出巨大的潜力，可以弥补传统全息天线的缺陷[2]。 RHS是一款超薄、轻便的表面天线，镶嵌有众多超材料辐射元件。具体来说，馈源生成的参考波以表面波的形式激发超表面，1 实现了基于印刷电路板 (PCB) 技术的 RHS 紧凑设计。根据全息图案，每个元件可以电控制参考波的辐射幅度，以产生所需的辐射图案2。因此，RHS无需笨重的机械运动装置和复杂的移相电路即可实现动态波束形成。它可以安装在移动平台（如火车、飞机、汽车）上，提供高吞吐量的数据服务3。

在文献中，RHS 的现有工作可大致分为硬件组件设计 [2] 和辐射方向图控制 [3]。在[2]中，提出了一种能够生成多光束辐射方向图的基于PCB的平行板波导RHS。在[3]中，RHS的辐射方向图控制算法已被开发用于旁瓣抑制。然而，大多数工作仅证明了 RHS 实现动态多波束转向的可行性。他们都没有研究全息波束形成对系统性能的影响。

这封letter是第一篇考虑 RHS 辅助的多用户通信的信函。我们提出了一种混合波束成形方案来支持配备 RHS 的 BS 和多个移动用户之间的通信。具体而言，BS处的数字波束形成和RHS处的全息波束形成被联合优化以最大化总速率。由于以下两个原因，这是一项艰巨的任务。首先，传统的相控模拟波束形成方案不适用于幅控全息波束形成。需要开发一种新的波束形成方案来处理受非常规实域幅度约束以及来自不同辐射元件的辐射波叠加的复杂域优化问题。其次，所有辐射元件之间与传播表面波同时耦合使全息波束形成设计变得复杂。为了应对这些挑战，我们设计了一种新颖的幅度控制算法，其中还导出了封闭式最优全息波束形成方案。

RECONFIGURABLE HOLOGRAPHIC SURFACE

本节我们介绍RHS的物理结构和全息原理。

Physical Structure

RHS是一种特殊的漏波天线。它主要由$K$个馈源(feed)、平行板波导(waveguide,)、$M\times N$离散亚波长超材料辐射单元平面阵列和辐射幅度控制器四部分组成，如图1（a）所示。具体来说，馈源嵌入 RHS 的底层，以生成携带接收器预期信号的参考波。产生的参考波直接注入波导。与传统天线阵列相比，这种结构可实现超薄 RHS，传统天线阵列的馈源通常体积庞大且位于天线表面之外。平行板波导起到导波结构的作用，是参考波的传播介质。它限制并引导参考波以表面波的形式在其表面传播。超材料辐射元件由具有超常电磁特性或结构的人造复合材料制成，其电磁响应（如辐射幅度）可以通过磁或电偏置场智能控制[5]。在RHS中，波导表面有许多超材料辐射元件。每个辐射元件由在元件下方的波导上传播的参考波激励，并由辐射幅度控制器控制。
Fig1.(a) Schematic structure of RHS. (b) Geomet-
rical relation between the RHS and object beam.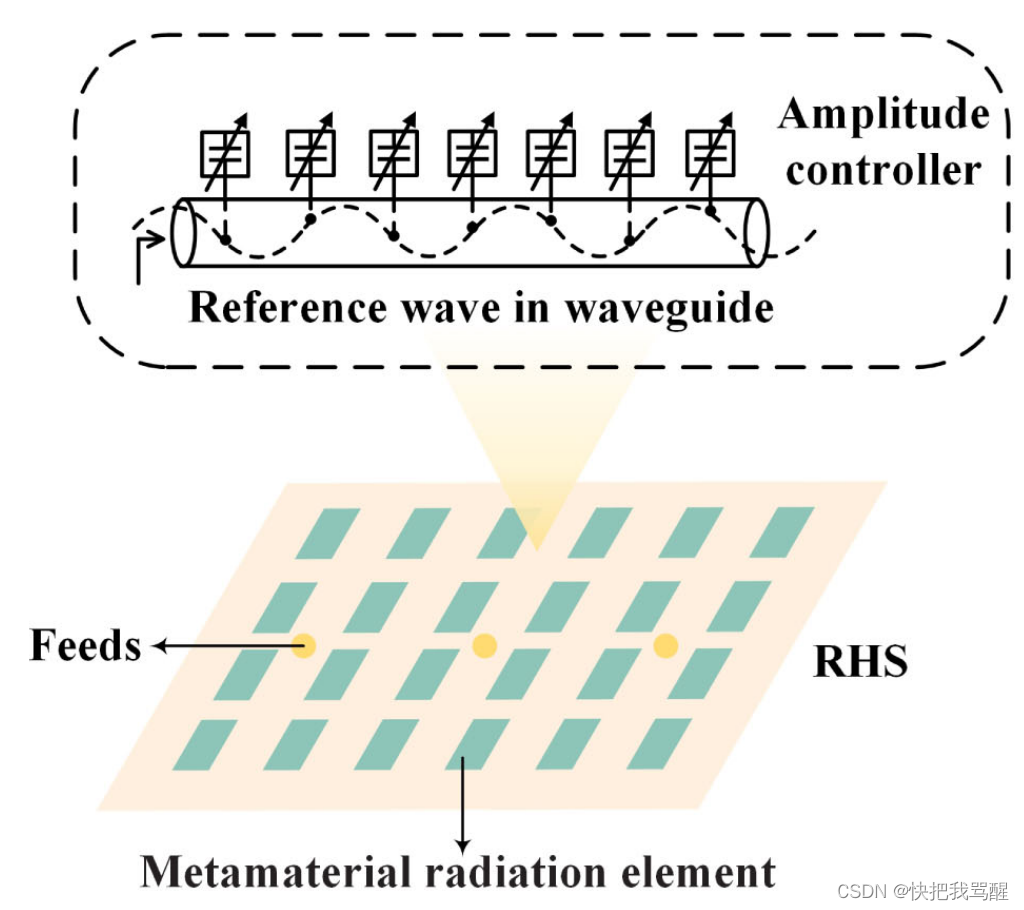

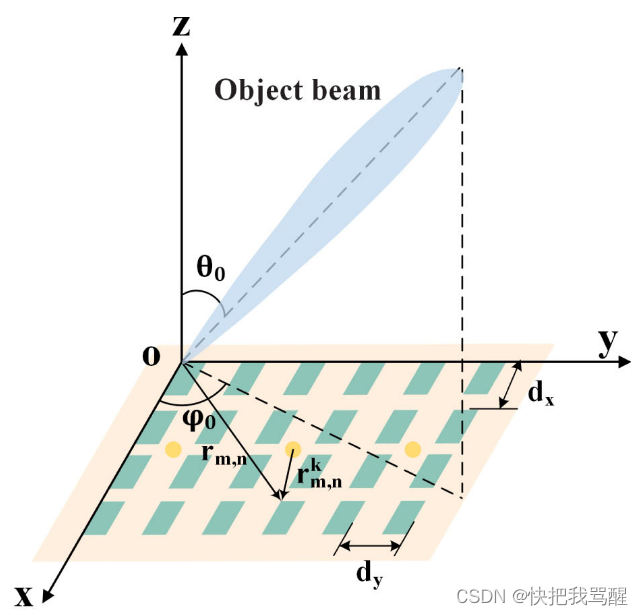
全息的原则

RHS的主要特点是构造全息图案，根据全息干涉原理记录参考波和物体波之间的干涉。利用全息图案，RHS可以有效控制参考波的泄漏以获得目标波。

We adopt the Cartesian coordinate where the $xoy$ plane coincides with the RHS, and the $z$ -axis is vertical to the RHS as shown in Fig. 1(b). At the $(m,n)$-th radiation element, the desired wave propagates in the direction $\left({\theta }_0,{\phi }_0\right)$ is ${\Psi }_{obj}\left({\mathbf{r}}_{m,n},{\theta }_0,{\phi }_0\right)=\exp (-j{\mathbf{k}}_f\left({\theta }_0,{\phi }_0\right).{\mathbf{r}}_{m,n})$ , and the reference wave generated by feed $k$ is ${\Psi }_{ref}\left({\mathbf{r}}_{m,n}^k\right)=\exp \left(-j{\mathbf{k}}_s\cdot {\mathbf{r}}_{m,n}^k\right)$ , where ${\mathbf{k}}_f\left({\theta }_0,{\phi }_0\right)$ is the desired directional propagation vector in free space, ${\mathbf{k}}_s$ is the propagation vector of the reference wave, ${\mathbf{r}}_{m,n}$ is the position vector of the $(m,n)$ -th radiation element, and ${\mathbf{r}}_{m,n}^k$ the distance vector from the feed $k$ to the $(m,n)$ -th radiation element. The interference between the reference wave and the desired objec t wave is defined as

$${\Psi }_{\text{intf }}\left({\mathbf{r}}_{m,n}^k,{\theta }_0,{\phi }_0\right)={\Psi }_{obj}\left({\mathbf{r}}_{m,n},{\theta }_0,{\phi }_0\right){\Psi }_{ref}^{\ast }\left({\mathbf{r}}_{m,n}^k\right)$$

因此，当全息图案受到参考波激励时，有${\Psi }_{intf}{\Psi }_{ref}\propto {\Psi }_{obj}{\left|{\Psi }_{ref}\right|}^2$，从而产生沿$\left({\theta }_0,{\phi }_0\right)$方向传播的波。

为了记录干涉图案，RHS采用幅度控制方法来构造全息图案，而不是传统的相移。请注意，${\Psi }_{\text{intf }}\left({\mathbf{r}}_{m,n}^k,{\theta }_0,{\phi }_0\right)$的实部，即 $\cos \left({\mathbf{k}}_f\left({\theta }_0,{\phi }_0\right)\cdot {\mathbf{r}}_{m,n}-{\mathbf{k}}_s\cdot {\mathbf{r}}_{m,n}^k\right)$ 包含物体波和参考波。第$(m,n)$个辐射单元产生辐射方向为$\left({\theta }_0,{\phi }_0\right)$的物波的归一化辐射幅度可以由下式给出:

$$\mathrm{M}\left({\mathbf{r}}_{m,n}^k,{\theta }_0,{\phi }_0\right)=\frac{\mathrm{Re}\left[{\Psi }_{intf}\left({\mathbf{r}}_{m,n}^k,{\theta }_0,{\phi }_0\right)\right]+1}{2}$$

根据(2)，**当辐射元件中参考波的相移与物波的相移显着不同时，要求该元件向自由空间辐射很少的能量。相反，如果参考波的相移接近物波的相移，则需要该元件将大量能量辐射到自由空间中以生成所需的辐射图。**因此，与传统的相控波束形成依靠控制沿阵列每个天线传播的电磁波的相位不同，全息波束形成是通过控制每个单元的辐射幅度来实现的，无需复杂的移相电路。

系统模型

符号化通信模型

the intended signal vector for $L$ mobile users: $\mathbf{s}\in {\mathcal{C}}^{L\times 1}$
信号到馈源$\mathbf{V}\in {\mathcal{C}}^{K\times L}$
馈源到$M\times N$的阵列$\mathbf{M}\in {\mathcal{C}}^{MN\times K}$
信道${\mathbf{H}}_l\in {\mathcal{C}}^{J\times MN}$
${\mathbf{W}}_l\in {\mathcal{C}}^{J\times 1}$用于接收端均衡（这里应该用小写w）
$J$ number of data streams($J$是接收端每个用户的ULA天线数)
$K$ number of feeds

It is required that the number of RF chains in the hybrid architecture should
be greater than or equal to the number of active data streams [25]. In other
words, the number of feeds should also be no less than the number of active
data streams, i.e., $K\ge L$.

Without loss
of generality, it is assumed that each user has a uniform linear
array configuration with $J$ receive antennas and the antenna
spacing is denoted by $d_u$,

原文
Denote the intended signal vector for $L$ mobile users as $\mathbf{s}\in {.}^{L\times 1}$ , and thus, the transmitted signals of the BS is $\mathbf{Vs}$. The final signals received by mobile user $l$ can be given by

$$y_l={\mathbf{W}}_l^H{\mathbf{H}}_l\mathbf{M}{\mathbf{V}}_l{\mathbf{s}}_l+{\mathbf{W}}_l^H{\mathbf{H}}_l\mathbf{M}\sum _{l^{\prime }\ne l}{\mathbf{V}}_{l^{\prime }}{\mathbf{s}}_{l^{\prime }}+{\mathbf{W}}_l^H{\mathbf{z}}_l\text{\hspace{1em}(3)}$$

where ${\mathbf{H}}_l\in {\cdot }^{J\times MN}$ is the matrix of complex channel gains from the RHS to the $l$ -th user’s antennas, $\mathbf{M}$ is an $MN\times K$ matrix composed of element $\left\{{\mathrm{M}}_{m,n}\cdot e^{-j{\mathbf{k}}_s\cdot {\mathbf{r}}_{m,n}^k}\right\}$, $e^{-j{\mathbf{k}}_s\cdot {\mathbf{r}}_{m,n}^k}$ is the phase of the reference wave, ${\mathbf{V}}_l$ is the $l$-th column of $\mathbf{V}$ , and ${\mathbf{z}}_l\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }^2{\mathbf{I}}_J\right)$ is the additive white Gaussian noise. ${\mathbf{W}}_l$ is a $J\times 1$ \mathrm{RF} combiner at each mobile user, implemented using phase shifters such that ${\left|{\mathbf{W}}_l(j)\right|}^2=1$ . For convenience, we consider the uniform linear phased array at each mobile user, where ${\mathbf{W}}_l={\left[1,e^{j{k}_f{d}_s\sin {\varphi }_l},\dots ,e^{j{k}_f(J-1)d_s\sin {\varphi }_l}\right]}^T$, $d_s$ is the distance between antennas of the mobile user, and ${\varphi }_l$ is the angle of arrival of the signals with respect to the antenna array at mobile user $l$ . Therefore, the achievable rate of mobile user $l$ can be given by

$$R_l={\log }_2\left(1+\frac{{\left|{\mathbf{W}}_l^H{\mathbf{H}}_l\mathbf{M}{\mathbf{V}}_l\right|}^2}{J{\sigma }^2+{\sum }_{l^{\prime }\ne l}{\left|{\mathbf{W}}_l^H{\mathbf{H}}_l\mathbf{M}{\mathbf{V}}_{l^{\prime }}\right|}^2}\right)\text{\hspace{1em}(4)}$$

问题构建与算法设计

在本节中，我们首先制定 RHS 辅助多用户通信系统中的和速率最大化问题。然后我们开发一种联合优化算法来解决它。

合速率最大化问题构建

我们的目标是通过优化数字波束形成器 $\mathbf{V}$ 和全息波束形成器 { M m , n } \{M_{m,n}\} {Mm,n​} (或许我觉得应该写成这样 { M m , n } \{\mathbf{M}_{m,n}\} {Mm,n​}) 来最大化所有移动用户可实现的速率，如下所示：

max ⁡ { V , M m , n } ∑ l = 1 L R l s.t.  Tr ⁡ ( V H V ) ≤ P T , 0 ≤ M m , n ≤ 1 \max _{\left\{\mathbf{V}, \mathrm{M}_{m, n}\right\}} \sum_{l=1}^{L} R_{l} \quad \text { s.t. } \operatorname{Tr}\left(\mathbf{V}^{H} \mathbf{V}\right) \leq P_{T}, 0 \leq \mathrm{M}_{m, n} \leq 1 {V,Mm,n​}max​l=1∑L​Rl​ s.t. Tr(VHV)≤PT​,0≤Mm,n​≤1

其中PT是BS的总发射功率。

问题(5)与多用户MIMO系统中传统的相控波束形成设计不同，它是一个受非常规实域幅度约束以及来自不同辐射单元的辐射波叠加的复杂域优化问题。现有算法效果不佳，因为传统的模拟波束形成器是具有复域相位约束的复值矩阵[8]。为了解决上述挑战，我们考虑利用线性函数的仿射特性来消除（4）中的非凸项。具体来说，实值矩阵与其他矩阵（例如，（4）中给出的项$\left|{\mathbf{W}}_l^H{\mathbf{H}}_l\mathbf{M}{\mathbf{V}}_l\right|$）的内积模可以通过其元素的线性函数很好地近似。然后，全息波束成形优化问题可以重新表述为一系列具有封闭形式最优解的凸优化子问题。

feed的数量也应该不少于活动数据流的数量，即$K\ge L$。

为了有效地解决问题（5），我们将其分解为两个子问题，即优化$V$的数字波束成形和优化 { M m , n } \{M_{m,n}\} {Mm,n​}的全息波束成形。在接下来的小节中，我们首先提出两种算法来分别解决这两个子问题。然后总结了整体的迭代优化算法。

Digital Beamforming Design

由于ZF数字波束形成器可以获得接近最优的解决方案，因此我们考虑将ZF波束形成与功率分配一起作为BS处的低维数字波束形成器，以减轻用户间干扰[8]。然后，BS处的数字波束形成器可以由下式给出：

Holographic Beamforming Design

---

---

---

Reconfigurable Holographic Surface-Enabled Multi-User Wireless Communications: Amplitude-Controlled Holographic Beamforming

这篇论文主体内容一样，但是说的比较详细：
将问题分解为三个子问题

---

这里分别讨论三个子问题的求解

---

子问题1 数字波束赋形设计：采用注水算法

总结如下

---

子问题2 全息波束赋形设计

将问题从非凸放缩成凸，然后采用拉格朗日对偶
总计如下：

---

子问题3 Receive Combining Design