本文主要是介绍格密码学习笔记(七):密码学中的q相关格、简介SIS问题和LWE问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- Q Q Q-相关格
- Ajtai提出的单向函数(SIS)
- Regev提出的容错学习问题(LWE)
- 详细规约证明讲解
- 致谢
Q Q Q-相关格
密码学中通常使用符合以下2个性质的(随机)格 Λ \Lambda Λ构造具体方案:
- Λ ⊆ Z d \Lambda \subseteq \mathbb{Z}^d Λ⊆Zd是一个整数格;
- q Z d ⊆ Λ q \mathbb{Z}^d \subseteq \Lambda qZd⊆Λ对小整数 q q q取模后呈现周期性。
定义( q q q-相关格, q q q-ary lattice) 如果格 Λ \Lambda Λ满足 q Z n ⊆ Λ ⊆ Z n q \mathbb{Z}^n \subseteq \Lambda \subseteq \mathbb{Z}^n qZn⊆Λ⊆Zn,则称 Λ \Lambda Λ是一个 q q q-相关格。
注:这里的“-ary”有“与…有关”的意思,如果翻译为“阶”感觉怪怪的,如果是 q q q-阶群,感觉群里得有 q q q个元素,但定义里又没有体现。
什么是 q q q-相关格?举2个例子,对于任意 A ∈ Z q n × d \bm{A} \in \mathbb{Z}_q^{n \times d} A∈Zqn×d,有
- Λ q ( A ) = { x ∣ x m o d q ∈ A ⊤ Z q n } ⊆ Z d \Lambda_q(\bm{A}) = \{ \bm{x} | \bm{x} ~ \mathrm{mod} ~q \in \bm{A}^\top \mathbb{Z}^n_q \} \subseteq \mathbb{Z}^d Λq(A)={x∣x mod q∈A⊤Zqn}⊆Zd
- Λ q ⊥ ( A ) = { x ∣ A x = 0 m o d q } ⊆ Z d \Lambda^\perp_q(\bm{A}) = \{ \bm{x} | \bm{Ax} = \bm{0} ~ \mathrm{mod} ~ q \} \subseteq \mathbb{Z}^d Λq⊥(A)={x∣Ax=0 mod q}⊆Zd
定理 对于任意格 Λ \Lambda Λ,以下3个 q q q-相关格判断条件是等价的:
- q Z d ⊆ Λ ⊆ Z d q \mathbb{Z}^d \subseteq \Lambda \subseteq \mathbb{Z}^d qZd⊆Λ⊆Zd;
- 存在某些 A \bm{A} A满足 Λ = Λ q ( A ) \Lambda = \Lambda_q(\bm{A}) Λ=Λq(A)
- 存在某些 A \bm{A} A满足 Λ = Λ q ⊥ ( A ) \Lambda = \Lambda^\perp_q(\bm{A}) Λ=Λq⊥(A)
注意: 对于同一个 A \bm{A} A,格 Λ q ( A ) \Lambda_q(\bm{A}) Λq(A)和格 Λ q ⊥ ( A ) \Lambda^\perp_q(\bm{A}) Λq⊥(A)是不同的。而对于一个 A ∈ Z q n × d \bm{A} \in \mathbb{Z}^{n \times d}_q A∈Zqn×d,存在 A ′ ∈ Z q k × d \bm{A}' \in \mathbb{Z}^{k \times d}_q A′∈Zqk×d,使得 Λ q ( A ) = Λ q ⊥ ( A ′ ) \Lambda_q(\bm{A}) = \Lambda^\perp_q(\bm{A}') Λq(A)=Λq⊥(A′)。反过来亦如此。
对于同一个 A \bm{A} A, Λ q \Lambda_q Λq和 Λ q ⊥ \Lambda_q^\perp Λq⊥存在放缩对偶关系,即
- Λ q ( A ) ∨ = 1 q Λ q ⊥ ( A ) \Lambda_q(\bm{A})^\vee = \frac{1}{q} \Lambda^\perp_q(\bm{A}) Λq(A)∨=q1Λq⊥(A)
- Λ q ⊥ ( A ) ∨ = 1 q Λ q ( A ) \Lambda^\perp_q(\bm{A})^\vee = \frac{1}{q} \Lambda_q(\bm{A}) Λq⊥(A)∨=q1Λq(A)
Ajtai提出的单向函数(SIS)
Ajtai在1996年提出了基于 q q q相关随机格的单向函数(One-Way Function,OWF),并给出了安全性证明。这里的SIS是Short Integer Solution的缩写。该OWF构造如下图。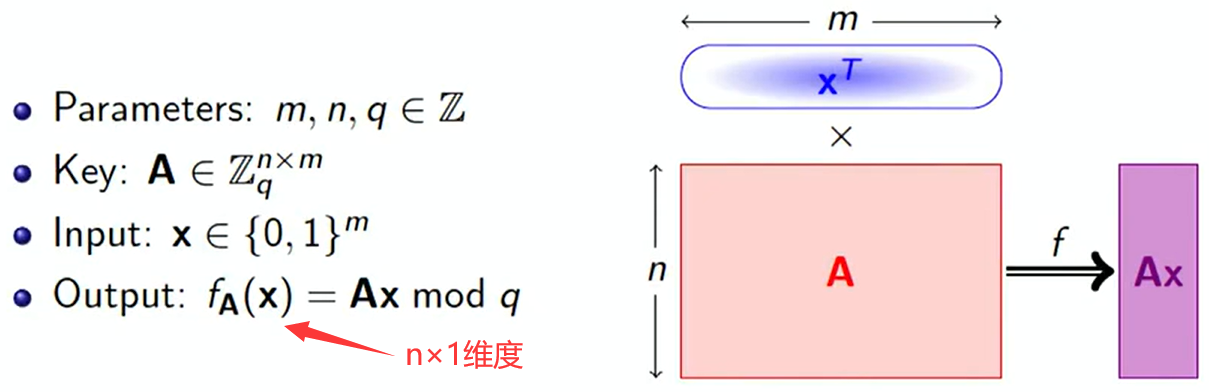
定理 对于 m > n l g q m > n ~ \mathrm{lg} ~ q m>n lg q,若SIVP问题在最差情况下依旧是困难的,那么 f A ( x ) = A x m o d q f_{\bm{A}}(\bm{x}) = \bm{Ax} ~ \mathrm{mod} ~ q fA(x)=Ax mod q是单向函数。
这里简要给出抗碰撞和单向的证明思路,后续公开课Daniele Micciancio教授有给出详细证明。
- f A ( x ) = A x m o d q f_{\bm{A}}(\bm{x}) = \bm{Ax} ~ \mathrm{mod} ~ q fA(x)=Ax mod q,这里的 x \bm{x} x是一个短向量,即一个二进制向量;
- f A f_{\bm{A}} fA的核是 q q q相关矩阵 Λ q ⊥ ( A ) \Lambda^\perp_q(\bm{A}) Λq⊥(A),注意: ∀ v ∈ Λ q ⊥ ( A ) \forall \bm{v} \in \Lambda^\perp_q(\bm{A}) ∀v∈Λq⊥(A),有 f A ( v ) = 0 m o d q f_{\bm{A}}(\bm{v}) = \bm{0} ~ \mathrm{mod} ~ q fA(v)=0 mod q;
- 寻找碰撞 ( ( x , y ) s.t. f A ( x ) = f A ( y ) ) \big( (\bm{x}, \bm{y}) ~ \text{s.t.} ~ f_{\bm{A}}(\bm{x}) = f_{\bm{A}}(\bm{y}) \big) ((x,y) s.t. fA(x)=fA(y))等价于寻找一个短向量 ( v = x − y ) ∈ Λ q ⊥ ( A ) ( \bm{v} = \bm{x} - \bm{y} ) \in \Lambda^\perp_q(\bm{A}) (v=x−y)∈Λq⊥(A),这里相当于求解了 Λ q ⊥ ( A ) \Lambda^\perp_q(\bm{A}) Λq⊥(A)的SVP / SIVP问题;
- 对 f A ( x ) f_{\bm{A}}(\bm{x}) fA(x)求逆相当于求解伴随译码格式下的CVP问题,CVP问题的输入为 Λ q ⊥ ( A ) \Lambda^\perp_q(\bm{A}) Λq⊥(A)和 t ∈ x + Λ q ⊥ ( A ) \bm{t} \in \bm{x} + \Lambda^\perp_q(\bm{A}) t∈x+Λq⊥(A),伴随译码的定义可以翻阅《格密码学习笔记(六):格中模运算》。即已知 f A ( x ) f_{\bm{A}}(\bm{x}) fA(x),对其求逆得到一个长向量 t \bm{t} t, t \bm{t} t与 x \bm{x} x在 Λ q ⊥ ( A ) \Lambda^\perp_q(\bm{A}) Λq⊥(A)中对应同一个陪集,找到 x \bm{x} x,则 t − x \bm{t} - \bm{x} t−x即CVP问题的格点解;
- 若 f A f_{\bm{A}} fA是一个压缩函数,那么 x \bm{x} x的长度需要大于 1 2 λ 1 ( Λ q ⊥ ( A ) ) \frac{1}{2}\lambda_1(\Lambda^\perp_q(\bm{A})) 21λ1(Λq⊥(A))(这块个人不怎么理解)。
注意, S I S ≡ Approximate A D D \mathsf{SIS} \equiv \text{Approximate} ~ \mathsf{ADD} SIS≡Approximate ADD(绝对距离解码)。
Regev提出的容错学习问题(LWE)
Regev在2005年提出Learning With Errors(LWE)。Learning(学习) 这个词常见于机器学习中,一个完整的机器学习方法包括模型和学习算法两部分,这里的“学习”可以理解成“figure out”,即求解出问题的解(从中学到某种知识)。LWE问题定义如下图。
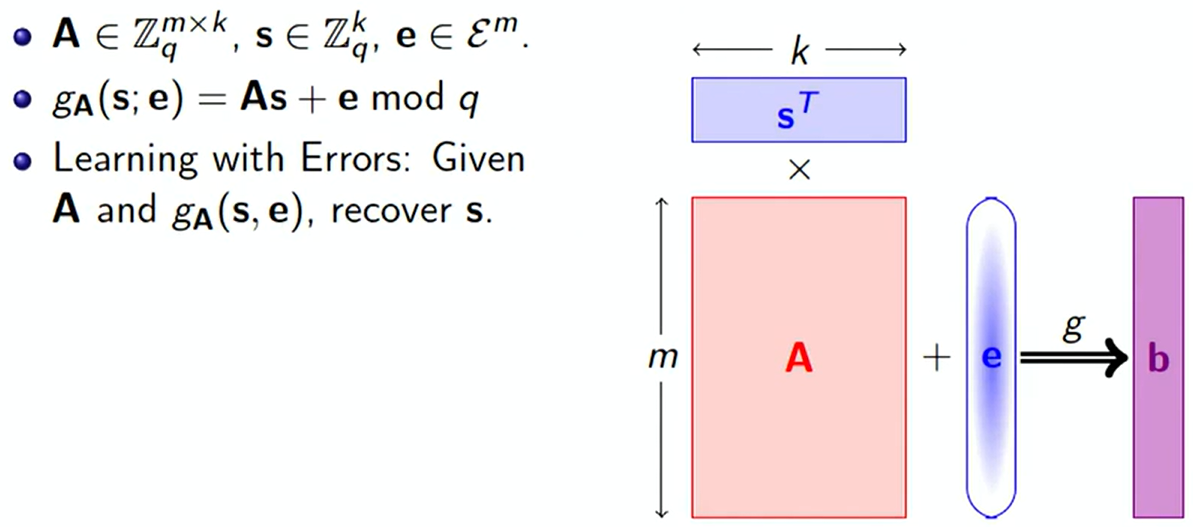
LWE与SIS看起来有点不一样,但某种程度上这两者之间是对偶关系。在LWE问题中,输入和错误向量 e \bm{e} e比SIS的向量短得多,得到的函数是单射的,安全性证明难度更大。
定理 若SIVP问题在最坏情况下是困难的,则函数 g A ( s , e ) g_{\bm{A}}(\bm{s}, \bm{e}) gA(s,e)在多数情况下难以求逆。
- 如果 e = 0 \bm{e} = \bm{0} e=0,那么 A s + e = A s ∈ Λ ( A ⊤ ) \bm{As} + \bm{e} = \bm{As} \in \Lambda(\bm{A}^\top) As+e=As∈Λ(A⊤),这里的转置请往上回翻 Λ q ( A ) \Lambda_q(\bm{A}) Λq(A)的定义;
- 若 e ≠ 0 \bm{e} \neq \bm{0} e=0,则相当于求解 q q q相关随机格 Λ ( A ⊤ ) \Lambda(\bm{A}^\top) Λ(A⊤)和随机向量 t = A s + e \bm{t} = \bm{As} + \bm{e} t=As+e的CVP问题(注意这里没有SIS中的伴随译码形式,所以某种程度上与SIS之间存在对偶关系);
- 一般情况下, e \bm{e} e的长度小于 1 2 λ 1 ( Λ ( A ⊤ ) ) \frac{1}{2}\lambda_1\big(\Lambda(\bm{A}^\top)\big) 21λ1(Λ(A⊤)),且 e \bm{e} e是唯一确定的。
注意, L W E ≡ Approximate B D D \mathsf{LWE} \equiv \text{Approximate} ~ \mathsf{BDD} LWE≡Approximate BDD(有界距离解码)。
详细规约证明讲解
推荐看Steven Yue大佬写的知乎文章(收录于稀有气体专栏)。
致谢
- Simons格密码公开课官网
Mathematics of Lattices - Simons Institute for the Theory of Computing - 哔哩哔哩中英双语视频(字幕组:重庆大学大数据与软件学院 后量子密码研究小组)
【中英字幕】Simons格密码讲座第1讲:格的数学定义_哔哩哔哩_bilibili - 其它格密码讲解课程和博文
Lattice学习笔记04:SIS与LWE问题
公开学习资料的无私奉献者
这篇关于格密码学习笔记(七):密码学中的q相关格、简介SIS问题和LWE问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






