本文主要是介绍格密码基础(3)-SIS,LWE,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
格密码基础(3)-SIS,LWE
这篇博文的主要内容是关于两个在现代格密码系统构造最基础的平均情况问题(SIS,LWE)以及他们的环变体(R-SIS,R-LWE)。
1.小整数解问题(SIS)
给定 m m m个 a 1 , … , a m a_1,\dots,a_m a1,…,am随机向量, a i ∈ Z q n a_i\in\mathbb Z^n_q ai∈Zqn。寻找一组非平凡解(简单理解:非零 ) z 1 , … , z m ∈ { − 1 , 0 , 1 } z_1,\dots ,z_m \in\{-1,0,1\} z1,…,zm∈{−1,0,1},使得 ∑ i = 0 m z i a i = 0 ∈ Z q n \sum \limits_{i=0}^mz_ia_i=0\in \mathbb Z^n_q i=0∑mziai=0∈Zqn。
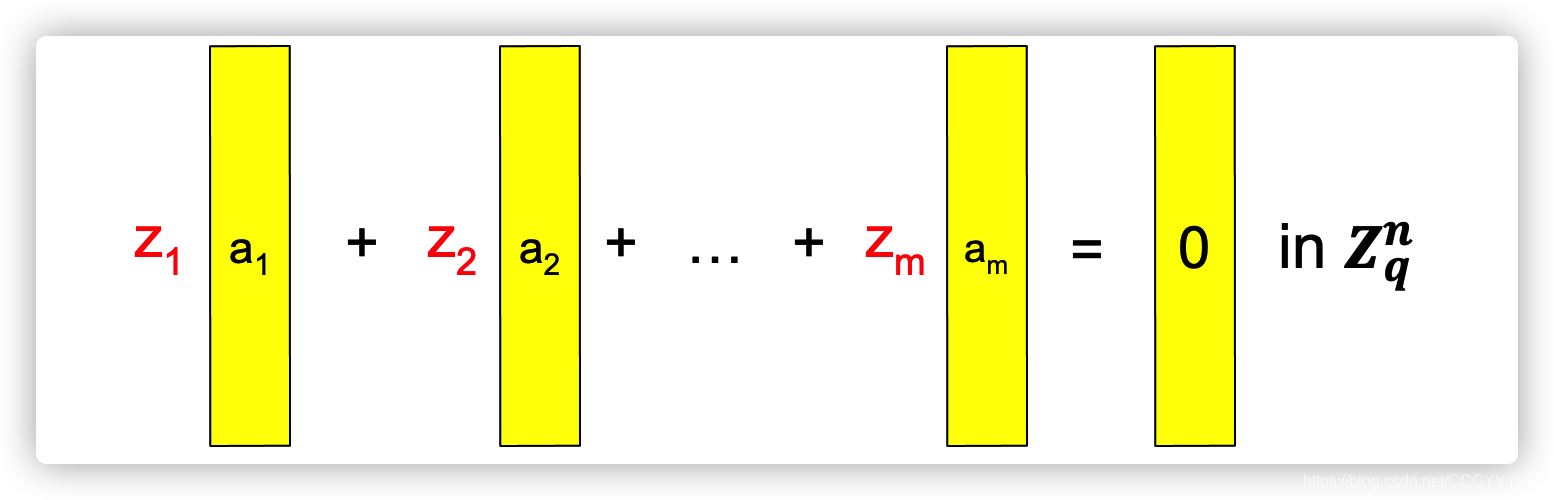
假设我们不对 z i z_i zi的大小进行限制,那么问题就不是困难的。
SIS问题可以被看作是平均情况下在 q q q阶 m m m维格上的SVP问题,这个 q q q阶 m m m维格:
L ⊥ ( A ) : = { z ∈ Z m : A z = 0 ∈ Z q n } ⊇ q Z m L^\perp(A):=\{z\in \mathbb Z^m:Az=0 \in \mathbb Z^n_q \} \supseteq q\mathbb Z^m L⊥(A):={z∈Zm:Az=0∈Zqn}⊇qZm
SIS问题就相当于是从格 L ⊥ ( A ) L^\perp(A) L⊥(A)中找到一个足够短的非零向量,且A为均匀随机选择的。
还有一个非齐次版本的SIS问题, ∑ i = 0 m z i a i = u ∈ Z q n \sum \limits_{i=0}^mz_ia_i=u\in \mathbb Z^n_q i=0∑mziai=u∈Zqn。这种情况下的解空间 L u ⊥ ( A ) L^\perp_u(A) Lu⊥(A)可以用 c + L ⊥ ( A ) c+L^\perp(A) c+L⊥(A)
来表示( c ∈ Z m c\in \mathbb Z^m c∈Zm, c c c并不要求短),这个版本和齐次版本的问题基本等价。
2.容错学习问题(LWE)
2.1简单理解
给出下列几个多项式:
$$
14⋅𝑠_1+15⋅𝑠_2+5⋅𝑠_3+2⋅𝑠_4≈8𝑚𝑜𝑑17\
13⋅𝑠_1+14⋅𝑠_2+14⋅𝑠_3+6⋅𝑠_4≈16𝑚𝑜𝑑17\
6⋅𝑠_1+10⋅𝑠_2+13⋅𝑠_3+1⋅𝑠_4≈3𝑚𝑜𝑑17\
\dots
$$
要求从中求出 s 1 , s 2 , s 3 , s 4 s_1,s_2,s_3,s_4 s1,s2,s3,s4。
假如所有的“≈”都换成“=”,那么这个问题将变得十分容易,只需要简单的高斯消元就可以解决。但是因为误差的引入,所以使得高斯消元无法解决现在的问题,(即从 A x = d Ax=d Ax=d求解 x x x,变成了 A x + e = d Ax+e=d Ax+e=d求解 x x x)。
2.2 LWE
关于LWE问题主要有两个版本的定义:搜索版本和判断版本。顾名思义,搜索版本就是从给出的问题中找到答案,而判断问题则主要是考察是否有能力区分。
在给出问题定义之前,先定义一个分布:
定义2.2.1 LWE分布
对于一组秘密向量 s ∈ Z q n s\in\mathbb Z^n_q s∈Zqn,LWE分布为 A s , χ ∈ Z q n × Z q A_{s,\chi}\in \mathbb Z^n_q\times\mathbb Z_q As,χ∈Zqn×Zq。从中随机选择一个 a ∈ Z q n a\in\mathbb Z^n_q a∈Zqn,选择一个向量 e ← χ e\leftarrow \chi e←χ,输出 ( a , b = < s , a > + e m o d q ) (a,b=<s,a>+e\mod q) (a,b=<s,a>+emodq)。
定义2.2.2 Search-LWE n , q , χ , m _{n,q,\chi,m} n,q,χ,m
给定 m m m个独立抽样$(a_i,b_i)\in\mathbb Z^n_q\times \mathbb Z_q 选 自 选自 选自A_{s,\chi} , 找 出 随 机 均 匀 变 量 ,找出随机均匀变量 ,找出随机均匀变量s$。
定义2.2.3 Decision-LWE n , q , χ , m _{n,q,\chi,m} n,q,χ,m
给定 m m m个独立抽样$(a_i,b_i)\in\mathbb Z^n_q\times \mathbb Z_q , 能 否 以 不 可 忽 略 优 势 来 分 辨 出 每 个 抽 样 是 来 自 : ( 1 ) ,能否以不可忽略优势来分辨出每个抽样是来自:(1) ,能否以不可忽略优势来分辨出每个抽样是来自:(1)A_{s,\chi} , s 是 随 机 均 匀 选 自 ,s是随机均匀选自 ,s是随机均匀选自\mathbb Z^n_q$,或者(2)均匀分布。
3.R-SIS
3.1 定义
环上的SIS变体的提出者是受到了NTRU密码方案的启发,主要增加的元素就是环R,这里的环就是NTRU中的所用的n维多项式环 R = Z [ X ] / ( f ( X ) ) , e . g . , f ( X ) = X n − 1 R=\mathbb Z[X]/(f(X)),e.g.,f(X)=X^n-1 R=Z[X]/(f(X)),e.g.,f(X)=Xn−1。
定义3.1 R-SIS q , β , m _{q,\beta,m} q,β,m
给定 m m m个 a 1 , … , a m a_1,\dots,a_m a1,…,am随机多项式, a i ∈ R q a_i\in R_q ai∈Rq,定义 a → ∈ R q m \stackrel{\rightarrow}{a}\in R^m_q a→∈Rqm。寻找非零向量 z → ∈ R m \stackrel{\rightarrow}{z} \in R^m z→∈Rm,**且满足 ∥ z → ∥ ≤ β \|\stackrel{\rightarrow}{z}\|\leq\beta ∥z→∥≤β**使得 ∑ i z i ⋅ a i = 0 ∈ R q \sum \limits_{i}z_i \cdot a_i=0\in R_q i∑zi⋅ai=0∈Rq,且 0 < max ∥ ( x i ) ∥ ≤ β 0<\max\|(x_i)\|\leq \beta 0<max∥(xi)∥≤β。
4.R-LWE
待续 … \dots …
这篇关于格密码基础(3)-SIS,LWE的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




