本文主要是介绍2、电路综合原理与实践---正实函数与策动电阻抗函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
2、电路综合原理与实践—正实函数与策动电阻抗函数
1、什么是策动点阻抗函数
需要先了解有一个拉普拉斯变换。其公式如下所示:
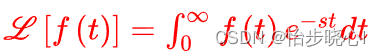
拉普拉斯变换公式能够将时域信号变换到频域,自然而然,它可以将电压、电流的时域波形变换到频域。即:
v(t) -> V(s)
i(t) -> I(s)
然后就可以得到策动点阻抗的表达式(p和s代表的是一个东西,简单来说就是电压除以电流):
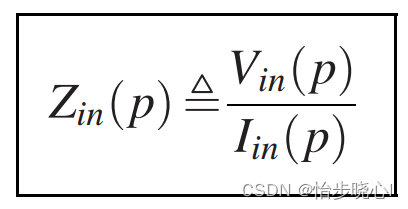
2、策动点阻抗函数性质
策动点阻抗都是针对端口而言的,譬如下面的电路图的输入端口的策动电阻抗:
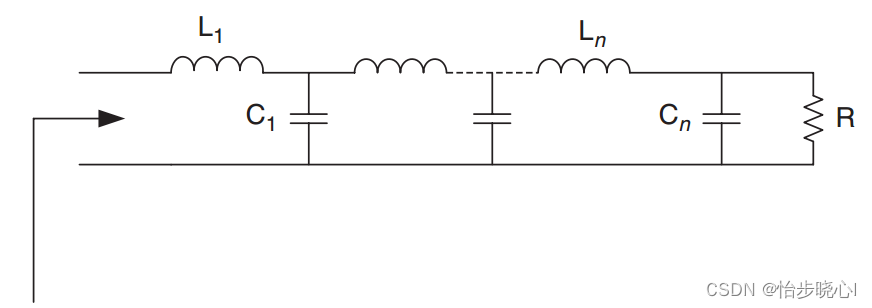
每个可实现的策动点阻抗都对应着实际的RLC电路实现,其策动点阻抗函数也必须遵循一定的数学规律。这个规律是什么呢?在吴宁老师的“电网络分析与综合”一书的7-3章“正实函数和无源性”中给出了答案,即:
由线性无源RLC元件构成的一端口网络的策动点阻抗函数必定是正实函数。
3、正实函数的判定

第一条判断非常简单,只要N和D中没有虚数项即可。
第二条判断比较麻烦,手撕需要使用罗斯-霍尔维茨数组(电网络分析与综合的7-3章“正实函数和无源性”),如果手里有Matlab可以使用roots函数结合定义进行判断。
比如我们需要判断下面这个函数是否是霍尔维茨多项式:
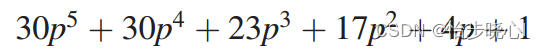
我们可以使用下面的代码:
N=[30 30 23 17 4 1];% Input
roots(N)
得到结果如下所示:

由此可见其所有零点都在左半平面,满足霍尔维茨多项式的定义。
第三条中的F(s)的虚轴的极点是单阶的,这等效于下面的分析。
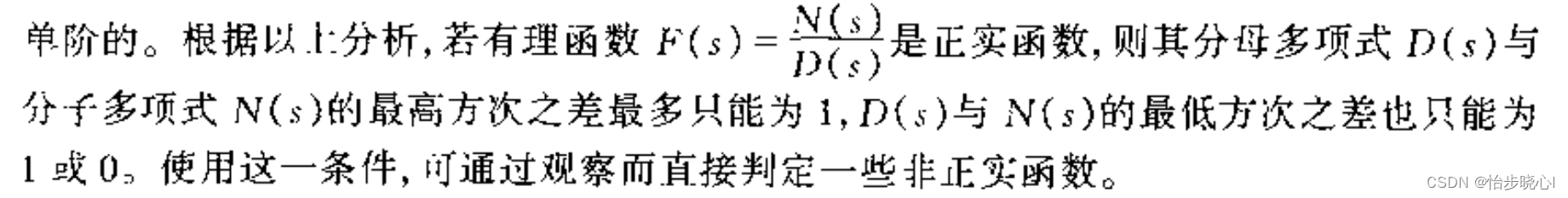
其余的判断都是需要进行计算,下面给出一个例子:
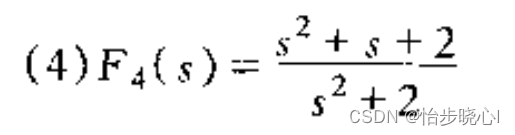

这篇关于2、电路综合原理与实践---正实函数与策动电阻抗函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






