BZOJ 1001 [BeiJing2006]狼抓兔子 （UVA 1376 Animal Run）

1001: [BeiJing2006]狼抓兔子

Time Limit: 15 Sec  Memory Limit: 162 MB
Submit: 24727  Solved: 6276
[Submit][Status][Discuss]

Description

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，

而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

 

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 

1:(x,y)<==>(x+1,y) 

2:(x,y)<==>(x,y+1) 

3:(x,y)<==>(x+1,y+1) 

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，

开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击

这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，

才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的

狼的数量要最小。因为狼还要去找喜羊羊麻烦.

Input

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值. 

第二部分共N-1行，每行M个数，表示纵向道路的权值. 

第三部分共N-1行，每行M-1个数，表示斜向道路的权值. 

输入文件保证不超过10M

Output

输出一个整数，表示参与伏击的狼的最小数量.

Sample Input

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

Sample Output

14

Source

[ Submit][ Status][ Discuss]

题目大意：在一个n×m的网格图中，要求从（1,1）到（n，m）不连通，那么最少断掉的边权之和。
题解：

　　直接看是网络流的最小割问题了。但是n×m个点=1000000，边更是3000000条，那么最小割显然不太好。因为是网格图，又是从（1,1）到（n，m）不连通，那么一定是从左边或下边，到上边或右边，那么我们就找一条从左下角到右上角的路径就可以断开连接了。把每一个三角形看成一个点，相邻三角形之间连接一条公共边边权的边，就可以跑最短路了，SPFA和Dij都可以。注意数组不要开小了。

具体见下图：

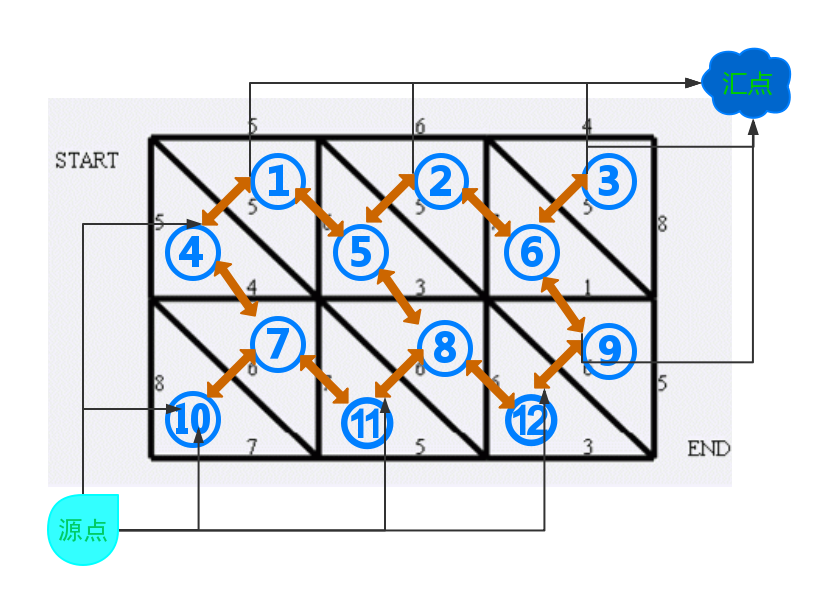
将每一个三角形编一个号，两个三角形之间连边，再将边界上的三角形连入源点和汇点即可了。

 

#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
#define fre(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout);
using namespace std;
const int MAXN=2500000,INF=0x3f3f3f3f;
int n,m,S,T,x,num,CASE;
int dis[MAXN];
int head[MAXN],to[MAXN*3],Next[MAXN*3],len[MAXN*3];
bool vis[MAXN];
struct ed
{
   int id,dis;
   bool operator <(const ed a)const{
      return dis>a.dis;
   }
};
void inti();
void add(int f,int t)
{
   Next[++num]=head[f];
   to[num]=t;
   len[num]=x;
   head[f]=num;
}
void Dij()
{
   priority_queue<ed>Q;
   memset(dis,0x3f3f3f3f,sizeof dis);
   memset(vis,0,sizeof vis);
   Q.push((ed){S,0}); dis[S]=0;
   while(!Q.empty())
      {
         ed u=Q.top(); Q.pop();
         if(u.id==T)break;
         vis[u.id]=1;
         for(int i=head[u.id];i;i=Next[i])
            {
               int v=to[i];
               if(vis[v])continue;
               if(dis[v]>dis[u.id]+len[i])
                  {
                     dis[v]=dis[u.id]+len[i];
                     Q.push((ed){v,dis[v]});
                  }
            }
      }
}
int main()
{
   while(scanf("%d%d",&n,&m)!=EOF)
      {
         if(n==m&&n==0)break;
         num=0;
         memset(head,0,sizeof head);
         inti();
         Dij();
         printf("Case %d: Minimum = %d\n",++CASE,dis[T]);
         //printf("%d\n",dis[T]);
      }
   return 0;
}
void inti()//连边，比较容易搞错。
{
   S=(n-1)*(m-1)*2+1; T=S+1;
   for(int i=1;i<=n;i++)
      for(int j=1;j<m;j++)
         {
            scanf("%d",&x);
            if(i==1) add(j,T),add(T,j);
            else if(i==n) add(S,(n-1)*(m-1)*2-(m-1)+j),add((n-1)*(m-1)*2-(m-1)+j,S);
            else
               {
                  int a=(i-1)*(m-1)*2-(m-1)+j;
                  int b=a+(m-1);
                  add(a,b); add(b,a);
               }
         }
   for(int i=1;i<n;i++)
      for(int j=1;j<=m;j++)
         {
            scanf("%d",&x);
            if(j==1) add(S,(i-1)*(m-1)*2+(m-1)+1),add((i-1)*(m-1)*2+(m-1)+1,S);
            else if(j==m) add((i-1)*(m-1)*2+(m-1),T),add(T,(i-1)*(m-1)*2+(m-1));
            else
               {
                  int a=(i-1)*(m-1)*2+(j-1);
                  int b=a+1+(m-1);
                  add(a,b); add(b,a);
               }
         }
   for(int i=1;i<n;i++)
      for(int j=1;j<m;j++)
         {
            scanf("%d",&x);
            int a=(i-1)*(m-1)*2+j;
            int b=a+(m-1);
            add(a,b); add(b,a);
         }
}