本文主要是介绍MATLAB中如何实现mesh三维图,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
当有两个自变量和一个因变量需要进行可视化时,可以使用mesh命令绘制双变量的三维图。
绘制三维图
以下是MATLAB官网中对于mesh命令的解读:
-
mesh(X,Y,Z)
mesh(X,Y,Z) 使用 Z 确定的颜色绘制线框网格,因此其颜色与曲面高度成比例,其中Z一定是矩阵,X,Y可以是矢量。如果 X 和 Y 为向量,length(X) = n 且 length(Y) = m,其中 [m,n] = size(Z)。在本示例中,(X(j), Y(i), Z(i,j)) 是线框网格线的交点;X 和 Y 分别对应于 Z 的列和行。如果 X 和 Y 为矩阵,则 (X(i,j), Y(i,j), Z(i,j)) 是线框网格线的交点。X、Y 或 Z 中的值可以是数值、日期时间值、持续时间值或分类值。 -
mesh(Z)
mesh(Z) 使用 X = 1:n 和 Y = 1:m 绘制线框网格,其中 [m,n] = size(Z)。高度 Z 是在矩形网格上定义的单值函数。颜色与曲面高度成正比。Z 的值可以是数值、日期时间、持续时间或类别值。 -
mesh(…,C)
mesh(…,C) 使用矩阵 C 确定的颜色绘制线框网格。MATLAB® 对 C 中的数据执行线性转换,以便从当前颜色图获取颜色。如果 X、Y 和 Z 为矩阵,它们的大小必须与 C 相同。
举例:数据来自百度
x=[16 17.5 19 21 22 23.7];
y=[3 6 9 10 12];
z=[ 0.08 0.09 0.09 0.1 0.11 0.11;
0.04 0.05 0.06 0.08 0.1 0.15;
0.02 0.05 0.12 0.19 0.27 0.44;
0.03 0.06 0.2 0.35 0.46 0.62;
0.32 0.45 0.84 0.88 0.94 1.17];
figure;
mesh(x,y,z); %两个自变量,一个因变量
xlabel(‘自变量1’);
ylabel(‘自变量2’);
zlabel(‘因变量Z’);
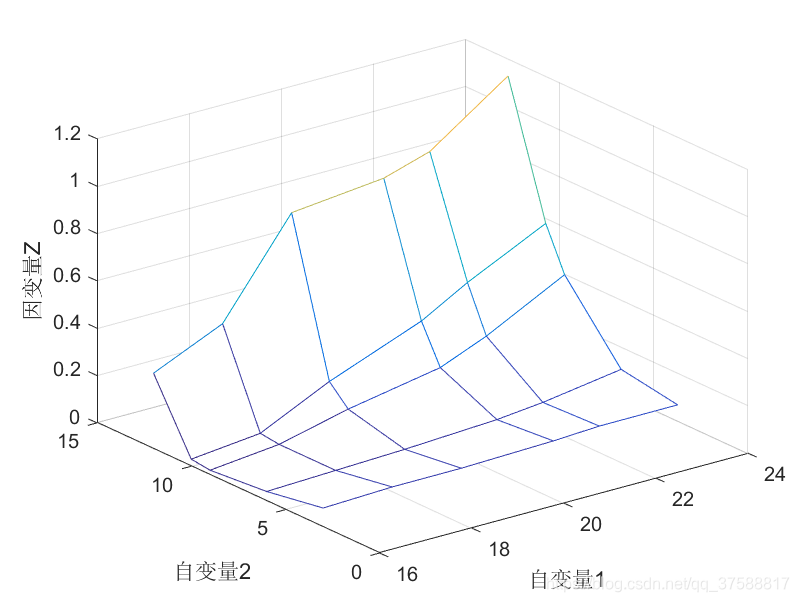
由于数据不够多,画出的图不是光滑,如果想让画出的曲面光滑一些,可以尝试使用griddata命令进行插值。
xx=linspace(16,23.7,100);%x是16到23.7的数列,长度为100,长度是可以随意调整的,越大越光滑
yy=linspace(3,12,100);%y是3到12的数列,长度为100
%数列长度可以根据改变,点数越多,数据点越密
zz=griddata(x,y,z,xx,yy’,‘cubic’);%三次多项式插值计算
figure;
mesh(xx,yy,zz);
xlabel(‘自变量1’);
ylabel(‘自变量2’);
zlabel(‘因变量Z’);
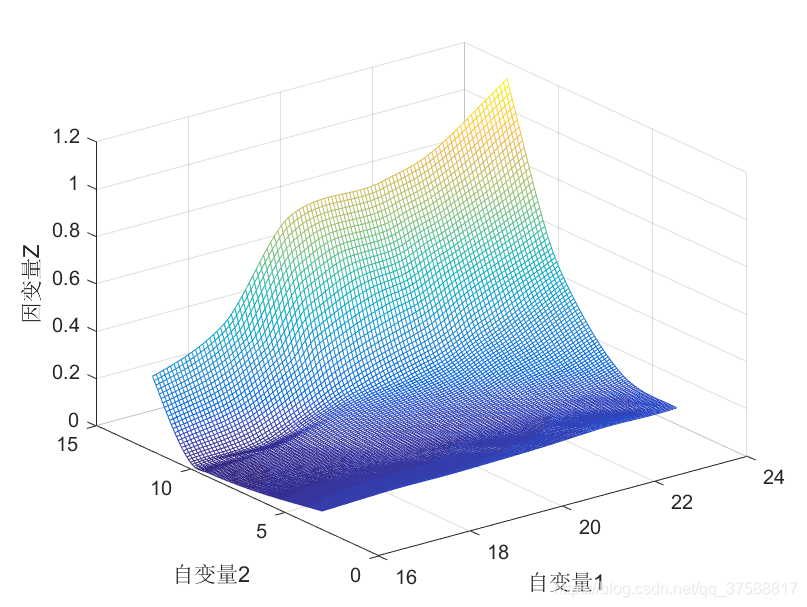
设置figure图的背景为白色
set(0,‘defaultfigurecolor’,‘w’)
调整视角
使用view命令来更改三维图的视角
调用格式 含义
view(az,el) 给三维空间图形设置观察点的方位角az与仰角el
view([az,el]) 同上
view([x,y,z]) 将点(x,y,z)设置为视点
view(2) 设置默认的二维形式视点,其中az = 0,el = 90,即从z轴上方观看
view(3) 设置默认的三维形式视点,其中az = -37.5, ell = 30
[az,el]=view 返回当前的方位角az与仰角el
方位角是 x-y 平面中的极坐标角,正值表示按逆时针方向旋转视点。仰角是位于 x-y 平面上方的角度(正角度)或下方的角度(负角度)。
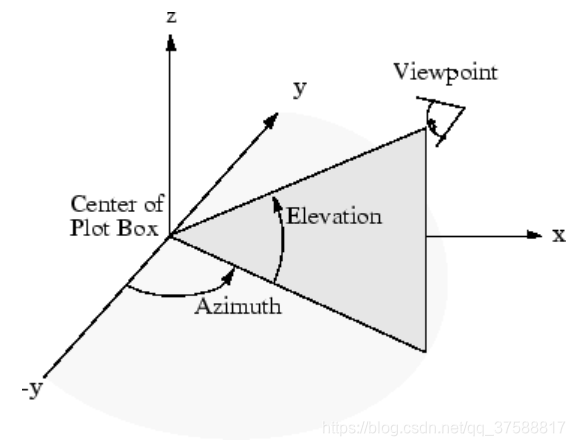
这篇关于MATLAB中如何实现mesh三维图的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





