【调制解调】PM 调相

说明

学习数字信号处理算法时整理的学习笔记。同系列文章目录可见 《DSP 学习之路》目录，代码已上传到 Github - ModulationAndDemodulation。本篇介绍 PM 调相信号的调制与解调，内附全套 MATLAB 代码。

1. PM 调制算法

1.1 PM 信号描述

用调制信号去控制载波的瞬时相位，使其按照调制信号的规律变化，当调制信号是模拟信号时，这个过程就被称为调相（PM）。在 FM 调频与 PM 调相的过程中，载波的幅度都保持恒定不变，而频率和相位的变化都表现为载波瞬时相位的变化，故把调频和调相统称为角度调制，与幅度调制技术相比，角度调制最突出的优势是其较高的抗噪声性能，然而获得这种优势的代价是角度调制占用比幅度调制信号更宽的带宽。PM 信号的时域表达式为：
$$s_{PM}(t)=Acos\left[{\omega }_{c}t+K_{p}m(t)\right]\text{\hspace{1em}(1)}$$

式中：$A$ 为载波恒定振幅，$K_p$ 为调相灵敏度（单位 $rad/V$），$m(t)$ 是调制信号（携带要发出去的信息），$cos{\omega }_{c}t$ 是载波，${\omega }_c$ 是载波角频率，与载波频率 $f_c$ 之间的关系为 ${\omega }_c=2\pi f_c$。由式 $(1)$ 可得 PM 信号相对于载波相位 ${\omega }_{c}t$ 的瞬时相位偏移为：
$$\phi (t)=K_{p}m(t)\text{\hspace{1em}(2)}$$
由 $(1)$ 式可知 PM 信号相对于载波相位 ${\omega }_{c}t$ 的瞬时相位偏移随 $m(t)$ 呈线性变化，比例系数为 $K_p$。PM 信号与 FM 信号有很多相同之处，如果预先不知道调制信号 $m(t)$ 的具体形式，则无法判断已调信号是 PM 信号还是 FM 信号。PM 信号的调相指数（调制指数）$\beta$ 被定义为最大的相位偏移：
$$\beta =K_p|m(t){|}_{max}\text{\hspace{1em}(3)}$$
若 $m(t)$ 为单一频率的正弦波（即 $m(t)=A_{m}cos(2\pi f_{m}t)$），则调制指数的表达式如下。
$$\beta =K_p|m(t){|}_{max}=K_p{A}_m\text{\hspace{1em}(4)}$$

1.2 PM 信号调制示例

与 FM 信号一样，PM 信号的调制方法也可分为 3 种，一种是直接调相法，一种是间接调相法，第三种是正交调制法。

（1）直接调相法

直接调相法是用调制信号 $m(t)$ 直接改变谐振回路的参数，使载波信号通过谐振回路时产生相移而形成调相波，最常用的直接调相电路是变容二极管调相器。

（2）间接调相法

间接调相电路比直接调相电路复杂，由于频率与相位之间存在微分与积分的关系，所以 FM 与 PM 之间是可以相互转换的。先对调制信号进行微分，然后对微分结果进行调频，就得到了调相信号，这种方式叫间接调相。先对调制信号进行积分，然后对积分结果进行调相，就得到了调频信号，这种方式叫间接调频。

（3）正交调制法

将 $(1)$ 式进行三角展开，可以得到：
$$\begin{array}{rl}{s}_{PM}(t)& =Acos\left[{\omega }_{c}t+K_{p}m(t)\right]\\ & =Acos({\omega }_{c}t)cos\left[K_{p}m(t)\right]-Asin({\omega }_{c}t)sin\left[K_{p}m(t)\right]\end{array}\text{\hspace{1em}(5)}$$
正交调制流程如下，其中第 2 步也可以先将 $I(t)$ 和 $Q(t)$ 组成一个复信号 $Z(t)=I(t)+iQ(t)$，然后乘以复载波 $exp(i{\omega }_{c}t)$，最后取实部，即 $s_{PM}(t)=Real\left[Z(t)exp(i{\omega }_{c}t)\right]$，两种方法是等价的。：

1. 对调制信号 $m(t)$ 分别取余弦和正弦，得到 $I$ 路数据 $I(t)=cos\left[K_{p}m(t)\right]$ 与 $Q$ 路数据 $Q(t)=sin\left[K_{p}m(t)\right]$。
2. 分别乘以载波 $Acos({\omega }_{c}t)$ 与 $-Asin({\omega }_{c}t)$ 后相加，得到 PM 信号 $s_{PM}(t)=I(t)Acos({\omega }_{c}t)-Q(t)Asin({\omega }_{c}t)$。

调制信号 $m(t)$ 可以是确知信号，也可以是随机信号。当 $m(t)$ 是确知信号时，不妨假设 $m(t)$ 的时域表达式如下：
$$m(t)=sin(2\pi f_{m}t)+cos(\pi f_{m}t)\text{\hspace{1em}(6)}$$
各调制参数取值：$A=1$，$f_m=2500Hz$，$\beta =4$，$f_c=20000Hz$。信号采样率 $f_s=8f_c$，仿真总时长为 $2s$。PM 调制效果如下图所示（为了美观，时域只显示前 500 个点），调制信号 $m(t)$ 双边幅度谱有四根离散谱线（$\pm 2500Hz$、$\pm 1250Hz$），载波 $c(t)$ 的双边幅度谱有两根离散谱线（$\pm 20000Hz$），代码详见附录 main_modPM_example.m 与 mod_pm.m，设置 beta = 4 即可。

2. PM 解调算法

解调是调制的逆过程，其作用是从接收的已调信号中恢复原基带信号（即调制信号）。PM 解调时，可以先使用 FM 解调器，然后对解调结果进行积分。另一种思路是直接提取 PM 信号的相位信息，有希尔伯特变换法以及数字正交解调法。下面分别用几种不同方法对 1.2 节中确知信号的 PM 调制结果进行解调。

2.1 FM 解调积分法

FM 信号的解调详见本人同系列博客 【调制解调】FM 调频，内有 FM 解调器相关代码。这种方法的流程如下：

1. 第一步：进行 FM 解调。
2. 第二步：对 FM 解调结果进行积分。
3. 第三步：去除直流分量（减去自身均值）。

对 1.2 节中的 PM 信号，设定信噪比 $SNR=50dB$，解调效果如下，解调后幅度放大系数 $k=\overline{|m(t)|}/\overline{|\hat{m}(t)|}\approx 70439.28$，使用这个系数放大解调信号幅值，然后计算误差，有：$\sqrt{\sum |m(t_i)-k\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0388$。

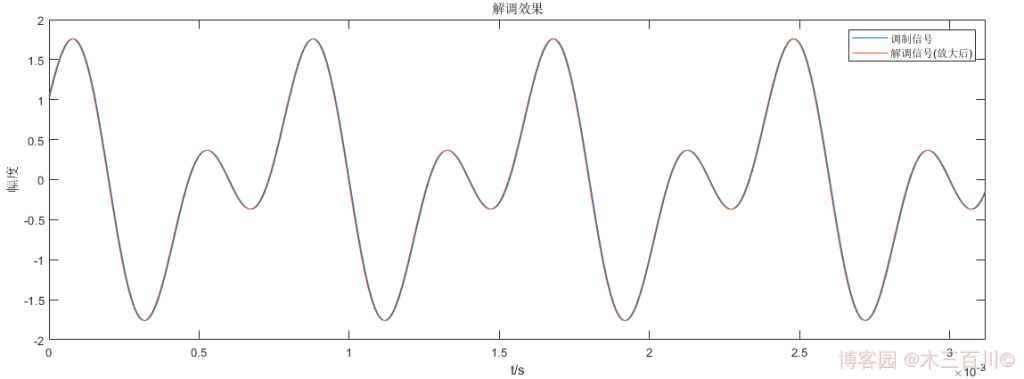
代码详见 demod_pm_method1.m 和 main_demodPM_example1.m，调频解调器的代码详见本人同系列博客 【调制解调】FM 调频。

2.2 希尔伯特求瞬时相位法

可以通过希尔伯特变换的方法求得 PM 信号的瞬时相位，然后减去由载波导致的线性分量 ${\omega }_{c}t$，获得非线性瞬时相位，也就是相对于载波相位 ${\omega }_{c}t$ 的瞬时相位偏移。这种方法的流程如下：

1. 第一步：计算 $s(t)$ 的希尔伯特变换，得到一个复信号（实部为 $s(t)$，虚部为其希尔伯特变换结果），对所得复信号求相位角并去卷叠，得到 PM 信号的瞬时相位 $\varphi (t)$。
2. 第二步：减去由载波导致的线性分量 ${\omega }_{c}t$ 以及载波初相 ${\phi }_0$，得到解调结果 $m_o(t)=\varphi (t)-{\omega }_{c}t-{\phi }_0$。

对 1.2 节中的 PM 信号，设定信噪比 $SNR=50dB$，解调效果如下，解调后幅度放大系数 $k=\overline{|m(t)|}/\overline{|\hat{m}(t)|}\approx 0.44$，使用这个系数放大解调信号幅值，然后计算误差，有：$\sqrt{\sum |m(t_i)-k\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0010$。

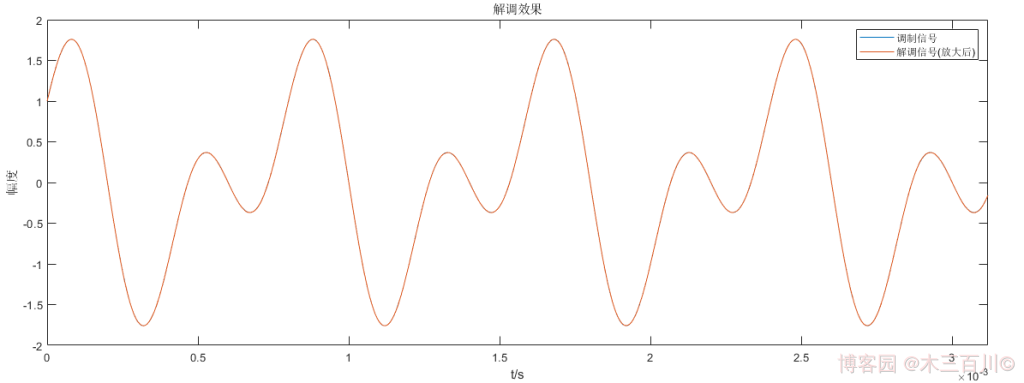
代码详见 demod_pm_method2.m 和 main_demodPM_example2.m。

2.3 数字正交解调

数字正交解调属于相干解调的一种，但这种方法具有较强的抗载频失配能力，不要求相干载波严格的同相。PM 数字正交解调一般有以下四个步骤：

1. 第一步：乘以正交相干载波得到 $s_I(t)$ 与 $s_Q(t)$，即 $s_I(t)=s(t)cos({\omega }_{c}t+{\varphi }_0)$，$s_Q(t)=-s(t)sin({\omega }_{c}t+{\varphi }_0)$。
2. 第二步：低通滤波器滤除 $s_I(t)$ 与 $s_Q(t)$ 中的高频分量。
3. 第三步：通过反正切函数计算相位，得到解调结果 $m_o(t)=atan\left[\frac{s_Q(t)}{s_I(t)}\right]=km(t)+\Delta \varphi$。
4. 第四步：去除直流分量（减去自身均值）。

对 1.2 节中的 PM 信号，设定信噪比 $SNR=50dB$，解调效果如下，解调后幅度放大系数 $k=\overline{|m(t)|}/\overline{|\hat{m}(t)|}\approx 0.44$，使用这个系数放大解调信号幅值，然后计算误差，有：$\sqrt{\sum |m(t_i)-k\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0007$。

代码详见 demod_pm_method3.m 和 main_demodPM_example3.m。更改相干载波的初始相位为 ${\varphi }_0=\pi /4,\pi /2$ 后，解调效果依然很好；但更改相干载波的中心频率为 $0.8f_c,1.2f_c$ 后，解调效果变得很差，说明这种方法具有较好的抗载频相位失配能力。

3. PM 仿真（MATLAB Communications Toolbox）

MATLAB 的 Communications Toolbox 中提供了 PM 调制函数 pmmod，高斯白噪声函数 awgn，以及 PM 解调函数 pmdemod，可以很方便地完成 PM 信号仿真。使用这三个函数实现上面 1.2 节中确知信号 $m(t)$ 的 PM 调制解调（将调相指数 $\beta$ 改为 $1$），调制后加噪声的效果如下：

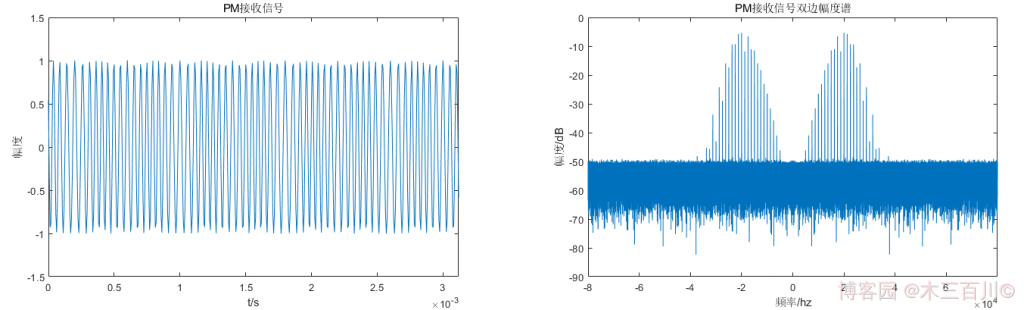
解调效果如下：

解调信号与调制信号波形基本重回，计算误差，有：$\sqrt{\sum |m(t_i)-\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0022$。代码详见附录 main_CommPM_example.m。

参考资料

[1] 楼才义,徐建良,杨小牛.软件无线电原理与应用[M].电子工业出版社,2014.

[2] 樊昌信,曹丽娜.通信原理.第7版[M].国防工业出版社,2012.

[3] 刘学勇.详解MATLAB/Simulink通信系统建模与仿真[M].电子工业出版社,2011.

[4] 王丽娜,王兵.卫星通信系统.第2版[M].国防工业出版社,2014.

附录代码

附.1 文件 mod_pm.m

function [ sig_pm ] = mod_pm(fc, beta, fs, mt, t, A)
% MOD_PM        PM 调相
% 输入参数：
%       fc      载波中心频率
%       beta    调频指数/调制指数
%       fs      信号采样率
%       mt      调制信号
%       t       采样时间
%       A       载波恒定振幅
% 输出参数：
%       sig_pm  调相(PM)实信号
% @author 木三百川% 计算调相灵敏度
Kp = beta/max(abs(mt));% 生成信号
ct = A*cos(2*pi*fc*t);           % 载波 
sig_pm = A*cos(2*pi*fc*t+Kp*mt); % PM调相信号% 绘图
nfft = length(sig_pm);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm));
subplot(3,2,1);
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('调制信号m(t)');
subplot(3,2,2);
plot(freq, 10*log10(fftshift(abs(fft(mt,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('调制信号m(t)双边幅度谱');subplot(3,2,3);
plot(t(1:plot_length), ct(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('载波c(t)');
subplot(3,2,4);
plot(freq, 10*log10(fftshift(abs(fft(ct,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('载波c(t)双边幅度谱');subplot(3,2,5);
plot(t(1:plot_length), sig_pm(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM调相信号s(t)');
subplot(3,2,6);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('PM调相信号s(t)双边幅度谱');end

附.2 文件 main_modPM_example.m

clc;
clear;
close all;
% PM 调制仿真(调制信号为确知信号)
% @author 木三百川% 调制参数
A = 1;                  % 载波恒定振幅
fm = 2500;              % 调制信号参数
beta = 4;               % 调相指数/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒% 采样时间
t = 0:1/fs:total_time-1/fs;% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);% PM 调制
[ sig_pm ] = mod_pm(fc, beta, fs, mt, t, A);

附.3 文件 lpf_filter.m

function sig_lpf = lpf_filter(sig_data, cutfre)
% LPF_FILTER    自定义理想低通滤波器
% 输入参数：
%       sig_data        待滤波数据
%       cutfre          截止频率，范围 (0,1)
% 输出参数：
%       sig_lpf         低通滤波结果
% @author 木三百川nfft = length(sig_data);
lidx = round(nfft/2-cutfre*nfft/2);
ridx = nfft - lidx;
sig_fft_lpf = fftshift(fft(sig_data));
sig_fft_lpf([1:lidx,ridx:nfft]) = 0;
sig_lpf = real(ifft(fftshift(sig_fft_lpf)));end

附.4 文件 demod_pm_method1.m

function [ sig_pm_demod ] = demod_pm_method1(sig_pm_receive, fc, fs, t, phi0)
% DEMOD_PM_METHOD1        PM 解调(FM 解调积分法)
% 输入参数：
%       sig_pm_receive      PM 接收信号，行向量
%       fc                  载波中心频率
%       fs                  信号采样率
%       t                   采样时间
%       phi0                相干载波初始相位
% 输出参数：
%       sig_pm_demod        解调结果，与 sig_pm_receive 等长
% @author 木三百川% 第一步：进行 FM 解调
[ sig_pm_demod ] = demod_fm_method4(sig_pm_receive, fc, fs, t, phi0);% 第二步：对 FM 解调结果进行积分
sig_pm_demod = cumtrapz(t, sig_pm_demod);% 第三步：去直流
sig_pm_demod = sig_pm_demod - mean(sig_pm_demod);end

附.5 文件 main_demodPM_example1.m

clc;
clear;
close all;
% PM 解调仿真(调制信号为确知信号，FM 解调积分法)
% @author 木三百川% 调制参数
A = 1;                  % 载波恒定振幅
fm = 2500;              % 调制信号参数
beta = 4;               % 调相指数/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒% 采样时间
t = 0:1/fs:total_time-1/fs;% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);% PM 调制
[ sig_pm_send ] = mod_pm(fc, beta, fs, mt, t, A);% 加噪声
snr = 50;               % 信噪比
sig_pm_receive = awgn(sig_pm_send, snr, 'measured');% FM 解调积分法
ini_phase = 0;
[ sig_pm_demod ] = demod_pm_method1(sig_pm_receive, fc, fs, t, ini_phase);% 绘图
nfft = length(sig_pm_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_pm_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('PM接收信号双边幅度谱');coef = mean(abs(mt))/mean(abs(sig_pm_demod));
fprintf('norm(调制信号 - %.2f * 解调信号)/norm(调制信号) = %.4f.\n', coef, norm(mt-coef*sig_pm_demod)/norm(mt));figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), coef*sig_pm_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号(放大后)');

附.6 文件 demod_pm_method2.m

function [ sig_pm_demod ] = demod_pm_method2(sig_pm_receive, fc, fs, t, phi0)
% DEMOD_PM_METHOD2        PM 解调(希尔伯特求瞬时相位法)
% 输入参数：
%       sig_pm_receive      PM 接收信号，行向量
%       fc                  载波中心频率
%       fs                  信号采样率
%       t                   采样时间
%       phi0                相干载波初始相位
% 输出参数：
%       sig_pm_demod        解调结果，与 sig_pm_receive 等长
% @author 木三百川% 第一步：使用希尔伯特变换计算瞬时相位
inst_phase = unwrap(angle(hilbert(sig_pm_receive)));% 第二步：去除载波分量
sig_pm_demod = inst_phase - 2*pi*fc*t - phi0;end

附.7 文件 main_demodPM_example2.m

clc;
clear;
close all;
% PM 解调仿真(调制信号为确知信号，希尔伯特求瞬时相位法)
% @author 木三百川% 调制参数
A = 1;                  % 载波恒定振幅
fm = 2500;              % 调制信号参数
beta = 4;               % 调相指数/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒% 采样时间
t = 0:1/fs:total_time-1/fs;% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);% PM 调制
[ sig_pm_send ] = mod_pm(fc, beta, fs, mt, t, A);% 加噪声
snr = 50;               % 信噪比
sig_pm_receive = awgn(sig_pm_send, snr, 'measured');% 希尔伯特求瞬时相位法
ini_phase = 0;
[ sig_pm_demod ] = demod_pm_method2(sig_pm_receive, fc, fs, t, ini_phase);% 绘图
nfft = length(sig_pm_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_pm_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('PM接收信号双边幅度谱');coef = mean(abs(mt))/mean(abs(sig_pm_demod));
fprintf('norm(调制信号 - %.2f * 解调信号)/norm(调制信号) = %.4f.\n', coef, norm(mt-coef*sig_pm_demod)/norm(mt));figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), coef*sig_pm_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号(放大后)');

附.8 文件 demod_pm_method3.m

function [ sig_pm_demod ] = demod_pm_method3(sig_pm_receive, fc, fs, t, phi0)
% DEMOD_PM_METHOD4        PM 数字正交解调/相干解调
% 输入参数：
%       sig_pm_receive      PM 接收信号，行向量
%       fc                  载波中心频率
%       fs                  信号采样率
%       t                   采样时间
%       phi0                相干载波初始相位
% 输出参数：
%       sig_pm_demod        解调结果，与 sig_pm_receive 等长
% @author 木三百川% 第一步：乘以正交相干载波
sig_pm_i = sig_pm_receive.*cos(2*pi*fc*t+phi0);
sig_pm_q = -sig_pm_receive.*sin(2*pi*fc*t+phi0);% 第二步：低通滤波
sig_pm_i_lpf = lpf_filter(sig_pm_i, fc/(fs/2));
sig_pm_q_lpf = lpf_filter(sig_pm_q, fc/(fs/2));% 第三步：计算相位
sig_pm_demod = unwrap(atan2(sig_pm_q_lpf, sig_pm_i_lpf));% 第四步：去直流
sig_pm_demod = sig_pm_demod - mean(sig_pm_demod);end

附.9 文件 main_demodPM_example3.m

clc;
clear;
close all;
% PM 解调仿真(调制信号为确知信号，数字正交解调)
% @author 木三百川% 调制参数
A = 1;                  % 载波恒定振幅
fm = 2500;              % 调制信号参数
beta = 4;               % 调相指数/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒% 采样时间
t = 0:1/fs:total_time-1/fs;% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);% PM 调制
[ sig_pm_send ] = mod_pm(fc, beta, fs, mt, t, A);% 加噪声
snr = 50;               % 信噪比
sig_pm_receive = awgn(sig_pm_send, snr, 'measured');% 数字正交解调
ini_phase = 0;
[ sig_pm_demod ] = demod_pm_method3(sig_pm_receive, fc, fs, t, ini_phase);% 绘图
nfft = length(sig_pm_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_pm_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('PM接收信号双边幅度谱');coef = mean(abs(mt))/mean(abs(sig_pm_demod));
fprintf('norm(调制信号 - %.2f * 解调信号)/norm(调制信号) = %.4f.\n', coef, norm(mt-coef*sig_pm_demod)/norm(mt));figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), coef*sig_pm_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号(放大后)');

附.10 文件 main_CommPM_example.m

clc;
clear;
close all;
% PM 调制解调仿真(使用Communications Toolbox工具箱)
% @author 木三百川% 调制参数
A = 1;                  % 载波恒定振幅
fm = 2500;              % 调制信号参数
beta = 1;               % 调相指数/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒% 采样时间
t = 0:1/fs:total_time-1/fs;% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);% FM 调制
ini_phase = 0;
sig_pm_send = A*pmmod(mt,fc,fs,beta,ini_phase);% 加噪声
snr = 50;               % 信噪比
sig_pm_receive = awgn(sig_pm_send, snr, 'measured');% PM 解调
[ sig_pm_demod ] = pmdemod(sig_pm_receive,fc,fs,beta,ini_phase);% 绘图
nfft = length(sig_pm_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_pm_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('PM接收信号双边幅度谱');figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_pm_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号');fprintf('norm(调制信号 - 解调信号)/norm(调制信号) = %.4f.\n', norm(mt-sig_pm_demod)/norm(mt));