本文主要是介绍3个5相乘列乘法算式_暑期小课堂:苏教版六年级数学《分数乘法》《分数除法》预习资料...,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
暑期课堂:苏教版六年级数学《分数乘法》《分数除法》预习资料,在家轻松学数学。大家好我是小梁老师,苏教版六年级数学之前我已经给讲了一单元的内容,一单元没有预习到的,前面的文章里有,大家可以自己翻看。这节课我们来预习苏教版六年级数学第二第三单元《分数乘法》和《分数除法》。再强调一次,这节课是苏教版六年级的预习课。

※第二单元《分数乘法》
第二单元《分乘法》数需要掌握的内容:
1、回忆乘法的意义。
2、会计算分数乘整数。会求一个数的几分之几是多少。
3、会计算分数乘分数。
4、会用分数乘法解决简单的实际问题。会确定题中的单位“1”。
5、知道什么是倒数。掌握求一个数倒数的方法。
6、会计算分数的连乘。
第二单元《分数乘法》知识点:
1、乘法的意义:几个相同加数的和可以用乘法表示。比如a+a+a=3×a
2、分数与整数相乘:
①同样对于分数乘以整数也可以用加法来计算。比如:3/10×3=3/10+3/10+3/10=9/10
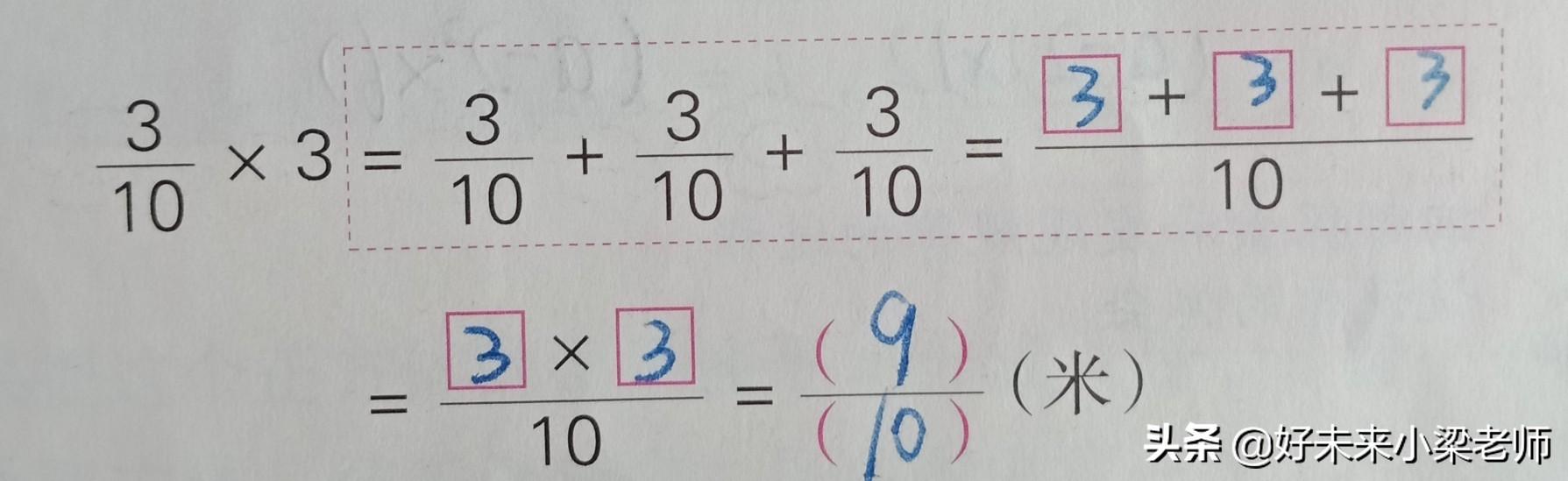
②整数可以看成分母是1的分数,分数乘整数的乘法一般按以下方法做:
①分子与分子相乘,然后约分。
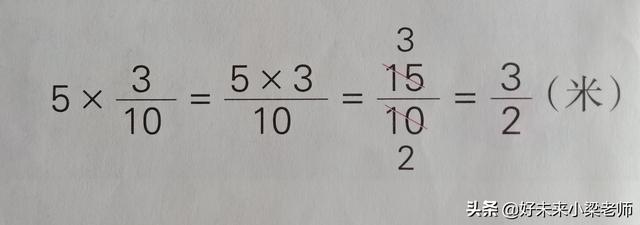
②先约分,然后再计算。
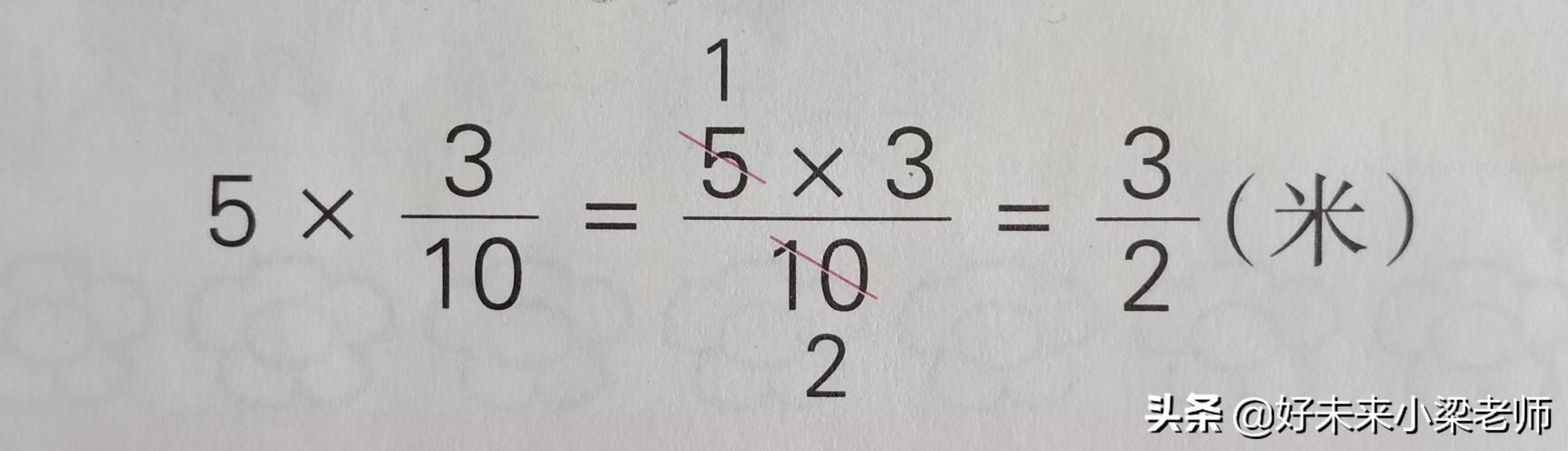
第②种方法计算更快。
3、分数与分数相乘:
分数和分数相乘,用分子相乘的积做分子,分母相乘的积做分母。
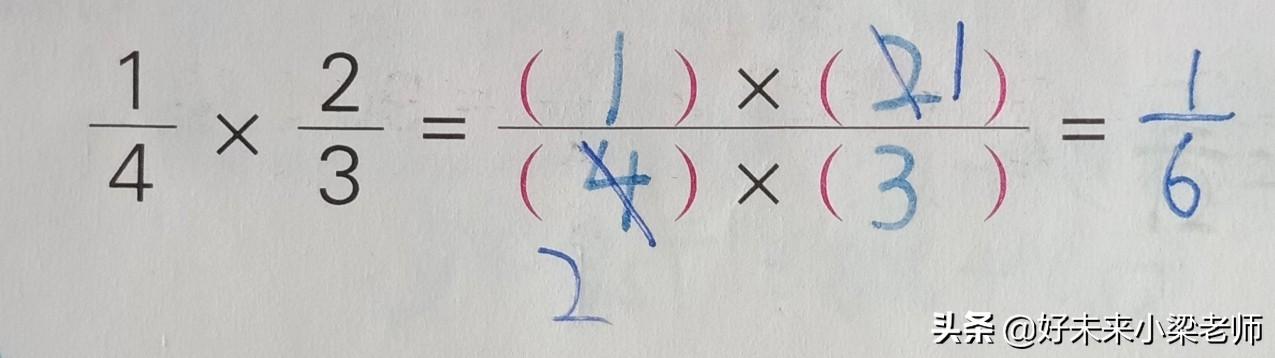
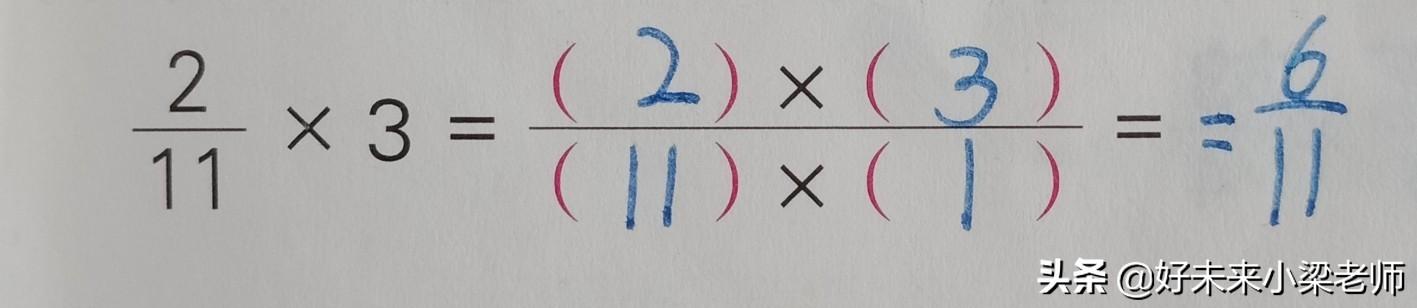
4、倒数:乘积是1的两个数互为倒数。
例如:3/8的倒数是8/3,8/3的倒数是3/8,3/8和8/3互为倒数。
8的倒数是1/8,1/6的倒数是6,1的倒数是1,0没有倒数。
《分数乘法相关题目》
1、一堆煤,每天烧1/40吨,5天一共烧多少吨?
2、一堆煤,每天烧1/40,5天一共烧这堆煤的几分之几?
3、25个4/5的和是多少?
4、小明有12本故事书,科技书的本数是故事书的7/4,文艺书的本数是科技书的2/3,小明有科技书和文艺书各多少本?
5、学校分给五年级360本图书,四年级分到的图书比五年级少1/12,六年级分到的图书比五年级多1/9。四年级比五年级少分多少本?六年级比五年级多分多少本?
6、根据条件,把数量关系式补充完整。
(1)小明家三月份比二月份多用电3/7。
_______的度数×3/7=_______的度数
(2)白兔的只数比灰兔少1/4。
_______的只数×1/4=_______的只数
7、

※第三单元《分数除法》
第三单元《分数除法》需要掌握内容:
1、分数除以整数的计算方法。
2、整数除以分数的计算方法。并且能计算分数连除和乘除混合运算的题目。
3、能列方程解答已知一个数的几分之几是多少,求这个数的简单实际问题。
4、掌握什么是“比”?会读会写比。知道比的各部分名称以及比与分数、除法的关系。
5、会应用比的基本性质求比值和化简比。
6、会用“比”的知识解决按比例分配的实际问题。
第三单元知识点:
1、分数除以整数的计算方法:
分数除以整数,可以转化成乘法计算。分数除以整数,等于分数乘这个整数的倒数。
例如:2/3÷3=2/3×1/3=2/9
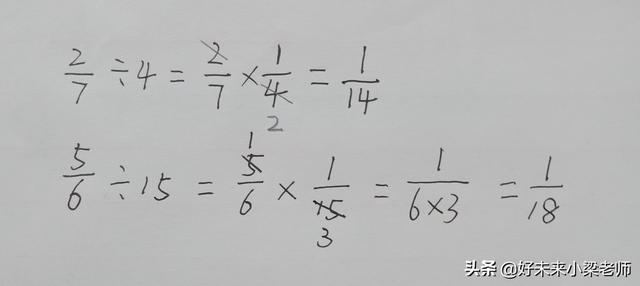
2、整数除以分数的计算方法:
整数除以分数也可以转化成乘法计算,整数除以分数,等于整数乘以这个分数的倒数。
例如:看书中的这个例题
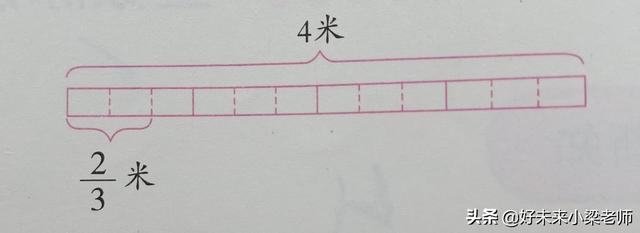
4米长的彩带,每2/3米剪一段,可以剪成多少段?
分析:这个题目中就是求4米中,有几个2/3,很显然应该用除法。
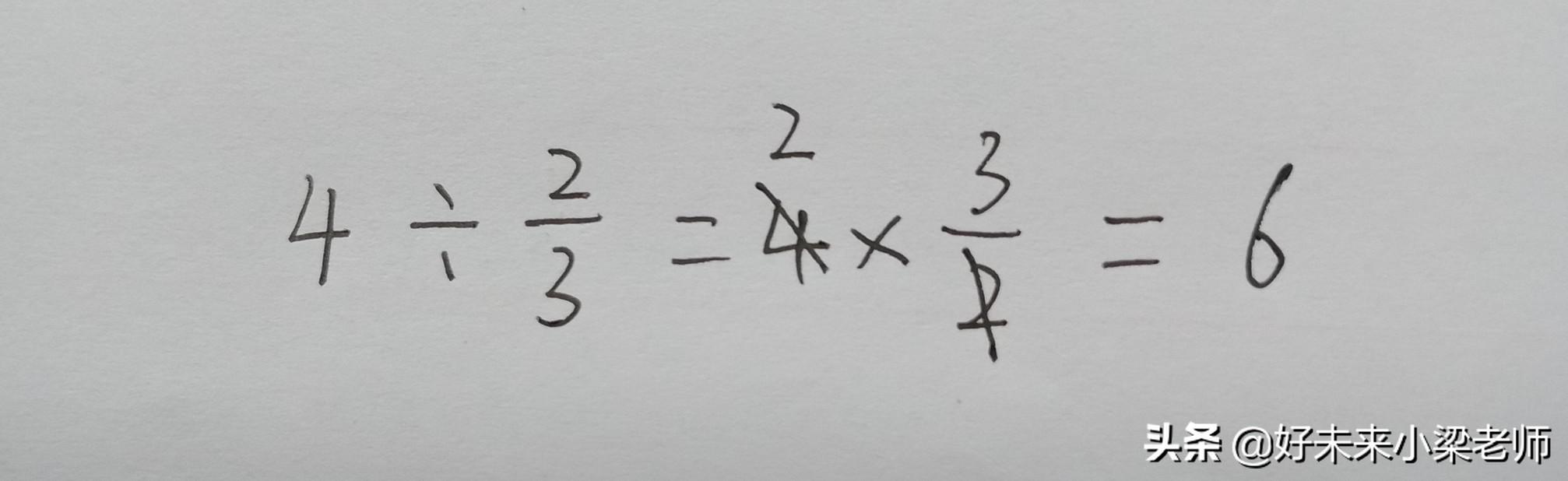
3、分数除以分数的计算方法:
分数除以分数同样可以转化成分数乘法来计算。甲数除以乙数(0除外),等于甲数乘乙数的倒数。也可以说:除以一个不为0的数,等于乘以这个数的倒数。
分数除法法则适用于一切除法。
比如举个简单的例子:
3÷2=1.5,
还可以这样计算:3÷2=3×1/2=3/2=1.5
4、比的意义。
两个数相除又可以叫做两个数的比。
⑴两个数相除可以用分数表示。
⑵两个数相除也可以用两个数的比表示。
例如:2÷3=2/3=2:3
其中“:”叫做比号,比号前面的数叫作比的前项,比号后面的数叫作比的后项。比前项除以后项所得的商叫做比值。
5、比和比值的联系和区别:
⑴比和比值的联系:比和比值都可以用分数形式表示,如3/5既可以表示3:5,又可以表示3:5的比值。
(2)比和比值的区别:
①比表示两个数的一种关系,比值是一个数值。
②比只能写成a:b或a/b的形式,比值可以是分数,也可以是小数、整数。
6、比的前项、后项和比值分列相当于除法算式或分数中的什么?比的后项可以是0吗?
比的前项相当于被除数,后项相当于除数,比号相当于除号。
比的前项相当于分子,比的后项相当于分母,比号相当于分数线。
所以比的后项不可以是0。
7、比的基本性质。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这是比的基本性质。
应用比的基本性质可以把一些比化成最简单的整数比。
(最简整数比指的是,比的前项和后项都是整数,并且互质)
将一个比化简成最简整数比的方法如下:
⑴将整数比化简成最简整数比:
如果前项和后项都是整数,前项和后项都除以他们的最大公因数,就可以化成最简整数比。
⑵将分数比化简成最简整数比:
如果前项和后项都是分数,则前项和后项都乘以分母的最小公倍数,把它转化成整数比,然后根据⑴化成最简整数比。
⑶将小数比化简成最简整数比:
如果前项和后项都是小数,那么前项和后项都要同时扩大相同的倍数,先转化成整数比,然后按照⑴化简成最简整数比。
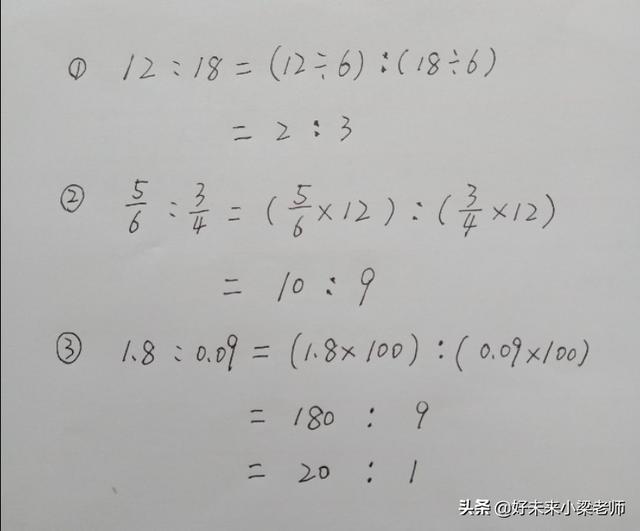
8、按比例分配问题。
也就是用比的知识解决实际问题。
看课本中的例题来领会一下如何利用比来解决实际问题。
例:把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?
解题分析:“红色与黄色方格数的比是3:2”,是说在30个方格里红色的方格占3份,黄色的方格占2份,一共是5份,即红色方格占总格数的3/5,黄色方格占总格数的2/5。
解题方法有两种:
思路一:把30个方格平均分成5份,3份涂红色,2份涂黄色。
3+2=5
30÷5×3=18(格)
30÷5×2=12(格)
思路二:红色方格占总格数的3/5,黄色方格占总格数的2/5。
30×3/5=18格
30×2/5=12格
练习:后面单独设一节课说除法的题目
这节课我们就说这么多,有关分数除法相关的题目下一节苏教版六年级数学课单独说,这节课的内容已经很多了,希望大家预习的时候课本内容和本节课所讲内容配合起来使用,预习效果更好。我是小梁老师,下节课见!

这篇关于3个5相乘列乘法算式_暑期小课堂:苏教版六年级数学《分数乘法》《分数除法》预习资料...的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!