本文主要是介绍模糊控制学习,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.模糊集合的定义
论域:所讨论的全体对象,用U等表示。
元素:论域中的每个对象,常用a,b,c,x,y,z表示。
集合:论域中具有某种相同属性的确定的,可以彼此区别的元素的全体,常用A,B表示。
经典集合:集合里面的元素非真即假。
模糊集合:模糊逻辑给集合中每一个元素赋予一个介于0-1之间的实数,描述其属于一个集合的强度,该实数称为元素属于一个集合的隶属度。集合中所有元素的隶属度全体够成集合的隶属度函数。
2.模糊集合表示方法
当论域中元素数目有限时,模糊集合的数学描述为:A={(x,μA(x)),x∈X}
μA(x):元素x属于模糊集A的隶属度,X是元素X的论域。
1.Zadeh表示法
论域是离散且元素数目有限
A=μA(x1)/x1+μA(x2)/x2+…+μA(xn)/(xn)=Σ(i=1 n)μA(xi)/xi
或
A={μA(x1)/x1,μA(x2)/x2,…,μA(xn)/xn
2.序偶表示法
3.向量表示法(隶属度为零也要写)
3.隶属函数
常见的隶属函数有正态分布、三角分布、梯形分布等
隶属函数确定方法
模糊统计法
专家经验法
二元对比排序法
基本概念扩充发
4.模糊关系及其合成
从论域X到论域Y的一个模糊关系R,用模糊矩阵表示R。
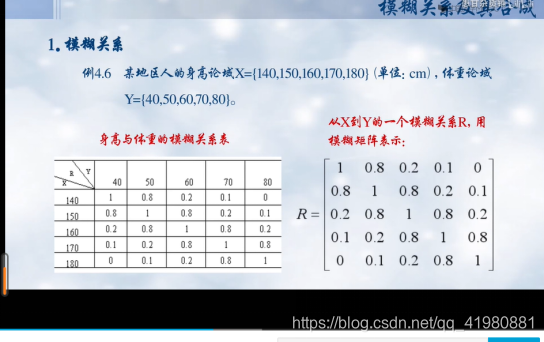
5.模糊知识表示
模糊规则:从条件论域到结论论域的模糊关系矩阵R。通过条件模糊向量与模糊关系R的合成进行模糊推理,得到结论的模糊向量,然后采用“清晰化”方法将结论转换为精确量。
“模糊决策”(“模糊判决”、“解模糊”或“清晰化”):由模糊推理得到的结论或者操作是一个模糊向量,转化为确定值的过程。
1)最大隶属度法

简单;但是忽略了其他元素隶属度也很大的情况。
2)加权平均判决法

3)中位数法

5.模糊推理的应用:

这篇关于模糊控制学习的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







