（论文解读）Unsupervised Salience Learning for Person Re-identification

论文解读之：

Unsupervised Salience Learning for Person Re-identification

这篇论文是关于行人重识别（ReID）方向的一篇论文，文中使用经典方法，通过匹配进行重识别。该论文发表在了2013CVPR上：

写在前面

在ReID领域，现有的很多算法都是有监督的，包括传统方法以及基于神经网络的方法。但是有监督的方法显然存在很多问题，从任何领域的发展趋势来看，都是无监督逐步代替有监督的过程，这不仅是因为无监督不需要打标签，还因为无监督更类似于大多数情况下人类的学习方式，更具有适应性与鲁棒性。在ReID领域，这个需求尤为重要。 因为当使用有监督的方法时，如果有一台相机的任何设置发生变化，就需要重新打标记，这是非常不美丽的，所以领域需要无监督的算法。
另外，ReID中还存在着一个重要的问题，即错对准（misalignment）。就是指在不同视角下看到的人处于不同的状态，如下图中，左图的人手机位于图片的中心，而右图中的人手机位于图片的边缘。这就意味着匹配时不能在两张图的同样位置进行匹配。
我们可以很轻松的想到一些导致错对准的因素：相机视角、行人姿势变化、人识别算法的bounding box不完美等。

基于这些，作者提出了一个无监督的算法进行ReID，按照论文的说法，本文的贡献如下：

贡献

• 提出了一种无监督框架，用于提取行人重识别的特征。
• 块匹配与邻接约束一起用于处理错对准问题。具有很高的准确性与灵活性。
• 通过无监督的方法得到显著性图，它对视点变化，姿势变化很敏感，并且是行人匹配的很有用的描述。比如仅具有显著上半身的人和仅具有显著下半身的人肯定不是同一个人。

作者所提到的显著性直观上来看其实就是指区分性，这两个图片好不好区分，这是一个感性的问题，作者将其量化为了显著性。比如，如果大多数人都穿着黑色裤子，那么腿部显然不是一个很好区分的位置，但如果有一个人穿了黄色裤子，那么这个人的腿部区分性就很高，即具有显著特征。

方法

总的来说，作者提出的方法流程如下：
首先对每个行人图像分块进行特征提取。
然后使用邻接约束搜索进行块匹配，同时得到显著性图像，这里作者提出可以两种方法实现这个步骤：KNN与OCSVM。
最后通过显著性图像进行重识别，使用了一种双向加权的方法。
接下来我们按照步骤一一分析。

行人特征提取

首先对一个行人的图像分块，对于每个块分别提取特征。分块的方法为取10×10的块，步长为4。提取到的特征包括两部分：颜色直方图与SIFT。
颜色直方图即对每个块提取其LAB颜色空间的颜色直方图，设置bin值为32，并且为了兼顾全局与局部特征，在三个下采样图像上进行提取，缩放因子为0.5、0.75、1。故得到的特征向量维度为32×3×3=288维。
SIFT特征是为了处理视点和光照变化，用作颜色直方图的补充特征。将每个块分为4×4个单元，将局部梯度量化为8个区间。与颜色直方图特征一样，SIFT特征也在三个下采样图像上进行提取，这样获得的SIFT特征总的维度为4×4×8×3=384维。
所有特征均使用L2正则化，最终得到的特征维度为288+384=672维，记为dColorSIFT。
在下文衡量相似度的时候，作者提出使用另一篇论文得到的结论：最小化距离不如最大化相似度。所以使用一个高斯函数将距离转化为相似度：
$$s(x,y)=exp(-\frac{d(x,y{)}^2}{2{\sigma }^2})$$
其中$s(x,y)$为相似度得分，$d(x,y)$为欧氏距离。

邻接约束搜索

获得了每个人的分块特征，接下来就需要进行匹配。匹配时采用邻接约束搜索，这是为了处理错对准问题的。
首先，我们定义$x_{m,n}^{A,p}$为相机A的第p个人图像中第m行n列的那个块。那么$x_{m,n}^{A,p}$在相机B的第q张人图像中的搜索集应该为第m行的所有块。又考虑到人识别算法的bounding box可能没有很好的框选人，所以要在竖直方向上增加一定的搜索空间，所以最终搜索集表示为：
S ^ ( x m , n A , p , x B , q ) = { T B , q ( b ) ∣ b ∈ N ( m ) } , \hat S(x^{A,p}_{m,n},x^{B,q})=\{\mathcal T^{B,q}(b) | b\in \mathcal N(m)\}, S^(xm,nA,p​,xB,q)={TB,q(b)∣b∈N(m)},
$$\forall x_{m,n}^{A,p}\in {\mathcal{T}}^{A,p}(m)$$
其中$\hat{S}(x_{m,n}^{A,p},x^{B,q})$表示$x_{m,n}^{A,p}$这个块在B相机的第q张人图像中的搜索集；${\mathcal{T}}^{B,q}(b)$表示$B$相机的第$q$张人图像中第$b$行的所有块； N ( m ) = { m − l , . . . , m , . . . , m + l } , m − l ≥ 0 , m + l ≤ M \mathcal N(m)=\{ m-l,...,m,...,m+l\},m-l\ge0,m+l\le M N(m)={m−l,...,m,...,m+l},m−l≥0,m+l≤M，式中$l$即为在竖直方向上放宽的范围。
这个公式通俗的讲就是：A相机的第p张人图像中第m行任意一个块在B相机的第q张人图像中的搜索集都是该图像中从$m-l$行到$m+l$行中的所有块。
这里$l$不能取太小也不能取太大，太小可能会导致没有搜索到正确的匹配，太大可能会导致错误匹配，如上半身匹配到下半身。通过实验，作者得出$l$取2最好。

显著性

通过上述的匹配，作者得出了每个图每个块的显著性得分，进而可以绘制出显著性图像。作者给出了两种显著性得分的计算方法：KNN与OCSVM。

KNN显著性得分

仍然讨论上述的问题：A相机中第p张人图像在B相机中进行重识别，若B相机中有$N_r$个人图像，则参考集大小即为$N_r$。
当$q$取1到$N_r$时，每个人图像都可以找到一个与$x_{m,n}^{A,p}$最相似的块，最终可以得到$N_r$个最相似的块，这个集合记为$X_{nn}(x_{m,n}^{A,p})$。但是在这些人中，肯定只有一个人与这个人对应，所以应该只有一个块是正确的块，其他都是错误的。那么如果这个块是一个区分性很大的块，则这$N_r$个块之间的距离应该很大，即错误的那些和那个正确的距离应该很大，所以作者提出使用第K个近邻表示显著性，这就是文章中的那个公式：
$$scor{e}_{knn}(x_{m,n}^{A,p})=D_k(X_{nn}(x_{m,n}^{A,p}))$$
那么重要的就是$k$的选取，作者提出$k=\alpha N_r$，其中$0<\alpha <1$。这样$k$的大小将会根据$N_r$的大小动态调整。根据实验，作者选取$\alpha =0.5$。
实际结果如下图，图a是使用偏最小二乘得到的显著性图，图b是使用作者的方法得到的显著性图。
绘图时，每个块中心位置的值为显著性值，然后进行上采样，得到如图b所示的显著性图。
可以看到作者提出的方法更能感应到对于重识别来说的重要特征。

OCSVM显著性得分

OCSVM是SVM的一类学习方法，论文中使用的OCSVM为SVDD，这是一种寻找超球面的方法，让这个超球面包括这一类数据，训练目标是最小化这个球的体积。
根据OCSVM的公式，可列得以下优化问题。

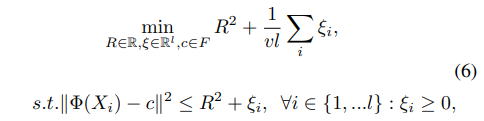
其中$R$和$c$为超球的半径和球心，$v$是用来调整学习偏向的，若$v$比较小，算法会尽量往球里塞更多的数据，如果$v$比较大，算法会尽量缩小球的体积。
通过QP优化的方法解该优化问题，即可得到决策函数：

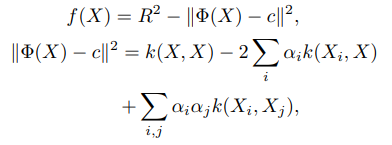
使用RBF核： K ( X , Y ) = e x p { − ∣ ∣ X − Y ∣ ∣ 2 / 2 σ 2 } K(X,Y)=exp\{-||X-Y||^2/2\sigma^2\} K(X,Y)=exp{−∣∣X−Y∣∣2/2σ2}，
按照论文《One-class svm for learning in image retrieval》中的说法，这个决策函数可以很好地获取特征分布的密度和形态。
可以想到，在提取出的$N_r$个最相似的块中，有很多是普通的难以区分的块，而一类SVM学习到的那个类就是这些难以区分的块，即那些离群点是区分性强的块，如下图所示。如果$x_{m,n}^{A,p}$是很好区分的，那么应该与学习到的类之间的距离较大。

所以作者将使这个函数值最高的块与$x_{m,n}^{A,p}$之间的距离定义为显著性得分。
$$scor{e}_{ocsvm}(x_{m,n}^{A,p})=d(x_{m,n}^{A,p},x^{\ast })$$
$$x^{\ast }=\underset{x\in X_{nn}(x_{m,n}^{A,p})}{\mathrm{argmax}}f(x)$$
OCSVM的显著性得分克服了超参数需要调整的问题。

重识别

最终到了重识别的步骤。
对于A相机中每个块$x_{m,n}^{A,p}$，在B相机的所有人图像（即所有q）中按照前面所说的邻接约束搜索找到最近邻的那个块$x_{i,j}^{B,q}$，用公式描述为：
$$x_{i,j}^{B,q}=\underset{\hat{x}\in \hat{S}(x_{m,n}^{A,p},x^{B,q})}{\mathrm{argmax}}s(x_{m,n}^{A,p},\hat{x})$$
然后相机B的所有q中，我们要找出哪个人是对应相机A中p人。作者采用最大化相似度函数的方法，即定义一个相似度函数$Sim$，使用两个人图像中所有的对应块计算相似度：
$$q^{\ast }=\underset{q}{\mathrm{argmax}}Sim(x^{A,p},x^{B,q})$$
其中$x^{A,p}$是相机A第p个人图像的块集合，$x^{B,q}$同理，即： x A , p = { x m , n A , p } m ∈ M , n ∈ N , x B , q = { x i , j B , q } i ∈ M , j ∈ N x^{A,p}=\{x^{A,p}_{m,n}\}_{m\in \mathcal M,n\in \mathcal N},x^{B,q}=\{x^{B,q}_{i,j}\}_{i\in \mathcal M,j\in \mathcal N} xA,p={xm,nA,p​}m∈M,n∈N​,xB,q={xi,jB,q​}i∈M,j∈N​
那么接下来的问题就是如何设计$Sim$函数，作者采用了双向加权的方法设计了一个比较复杂的$Sim$函数，如下：

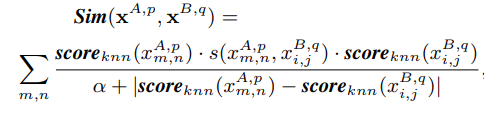
虽然复杂，但是设计的是有道理的。首先，由于显著性越高的块越容易进行正确的匹配，那么就要给这些快高一点的权重，所以分子上乘了两个块的$scor{e}_{knn}$。其次，相互匹配的两个块显著性得分应该是相近的，一个不显著的块和一个显著的块不可能是正确的匹配，所以分母上设计了两个块的显著性得分之差。

测试

作者在两个数据集上都进行了测试：VIPeR Dataset和ETHZ Dataset，在两个数据集上均取得了SOTA的效果。同时，OCSVM的显著性测量方法效果好于KNN的显著性测量方法。

总结思考

这篇论文创新性地使用了KNN距离与OCSVM衡量显著性得分，设计更加合理，且能够很好的解释。在重识别阶段没有直接采用相似度进行评判，而是设计$Sim$函数，通过双向加权的方法设计了一个新的相似度函数。可以想象到，这个$Sim$函数有效地解决了部分错误匹配的问题，即在某些情况下，两者显著性相差很远但是仍具有较高的相似度，这样的情况是匹配错误的情况，但如果不计算这个$Sim$函数，就会把这个情况认为是匹配正确，影响结果。
最重要的，这个方法属于无监督的方法，并不需要标记，极大地提高了适用性与实用性。