本文主要是介绍vivado 添加多循环路径,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
添加多循环路径
接下来,您将使用约束编辑器添加一个多循环路径。
1.双击树的“异常”类别下的“设置多周期路径”。
2.在“设置多周期路径”对话框中,将路径乘数设置为2。
3.在“通过”输入框中,键入以下字符串(或者,您可以复制和粘贴它
从这里):
[get_pins cpuEngine/or1200_cpu/or1200_alu/*]
请注意,Tcl命令显示在command字段中。
4.单击“确定”。
在<saved_constraints>的约束编辑器中添加了一个新的多循环路径
如下图所示。
4.单击“确定”。
在<saved_constraints>的约束编辑器中添加了一个新的多循环路径
如下图所示。
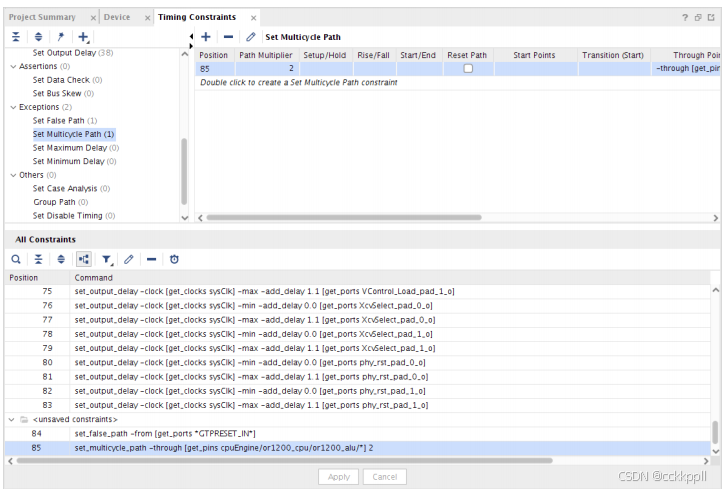
默认情况下,添加多周期路径会将设置时间推到指定数量
周期(N),但它也将保持时间推到N-1个周期。这通常不是预期的
这可能会导致Vivado工具花费大量时间修复大型持有违规行为。在这种情况下
您需要设置路径时钟。为了实现这一点,您需要在上定义另一个多循环路径
保持边为1,使得N-1为零。有关此情况的更多信息,请参阅
Vivado设计套件用户指南:使用约束(UG903)中的链接。
5.双击树的“例外”类别下的“设置多循环路径”一秒钟
时间。
注意:确保您之前输入的所有字段都已填写。
6.在“设置多循环路径”对话框中,将“路径倍数”更改为1。
7.选择选项选项卡。
8.在“设置/保持”下,选中“使用路径乘数”复选框。
9.使用下拉菜单选择保持(最小延迟)
周期(N),但它也将保持时间推到N-1个周期。这通常不是预期的
这可能会导致Vivado工具花费大量时间修复大型持有违规行为。在这种情况下
您需要设置路径时钟。为了实现这一点,您需要在上定义另一个多循环路径
保持边为1,使得N-1为零。有关此情况的更多信息,请参阅
Vivado设计套件用户指南:使用约束(UG903)中的链接。
5.双击树的“例外”类别下的“设置多循环路径”一秒钟
时间。
注意:确保您之前输入的所有字段都已填写。
6.在“设置多循环路径”对话框中,将“路径倍数”更改为1。
7.选择选项选项卡。
8.在“设置/保持”下,选中“使用路径乘数”复选框。
9.使用下拉菜单选择保持(最小延迟)
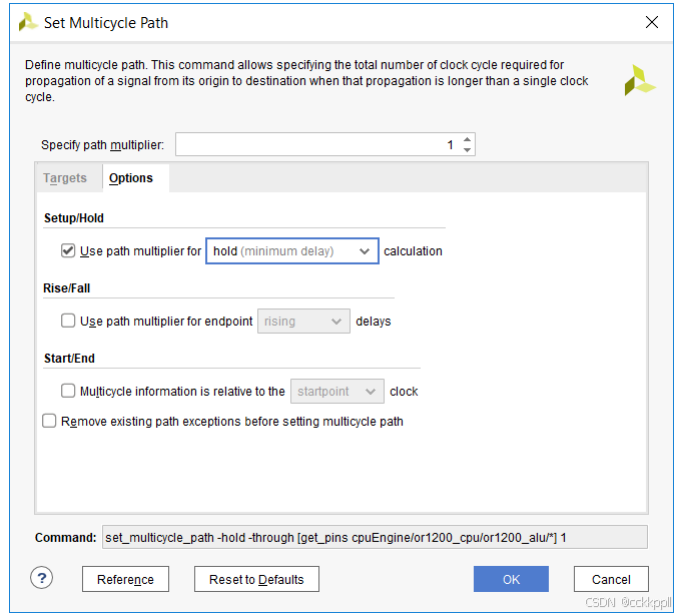
10.单击“确定”。
现在,您在内存中有一个完全受约束的设计。要将约束保存到磁盘,请继续
到步骤5:保存约束。
注意:有关添加多周期约束的原因的更多信息,请单击此处。了解更多信息
在检查工具是否应用了写入的异常时,请单击此处。
现在,您在内存中有一个完全受约束的设计。要将约束保存到磁盘,请继续
到步骤5:保存约束。
注意:有关添加多周期约束的原因的更多信息,请单击此处。了解更多信息
在检查工具是否应用了写入的异常时,请单击此处。
这篇关于vivado 添加多循环路径的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


