本文主要是介绍代码随想录算法训练营第五十天 | 98. 所有可达路径,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
98. 所有可达路径
思路
图的存储
邻接矩阵
邻接表
深度优先搜索
1.确认递归函数,参数
2.确认终止条件
3.处理目前搜索节点出发的路径
方法一: 邻接矩阵写法
方法二:邻接表写法
98. 所有可达路径
- 题目链接:卡码网题目链接(ACM模式)
文章讲解:代码随想录
【题目描述】
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
【输入描述】
第一行包含两个整数 N,M,表示图中拥有 N 个节点,M 条边
后续 M 行,每行包含两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径
【输出描述】
输出所有的可达路径,路径中所有节点的后面跟一个空格,每条路径独占一行,存在多条路径,路径输出的顺序可任意。
如果不存在任何一条路径,则输出 -1。
注意输出的序列中,最后一个节点后面没有空格! 例如正确的答案是
1 3 5,而不是1 3 5, 5后面没有空格!【输入示例】
5 5 1 3 3 5 1 2 2 4 4 5【输出示例】
1 3 5 1 2 4 5提示信息
用例解释:
有五个节点,其中的从 1 到达 5 的路径有两个,分别是 1 -> 3 -> 5 和 1 -> 2 -> 4 -> 5。
因为拥有多条路径,所以输出结果为:
1 3 5 1 2 4 5或
1 2 4 5 1 3 5都算正确。
数据范围:
- 图中不存在自环
- 图中不存在平行边
- 1 <= N <= 100
- 1 <= M <= 500
思路
图的存储
在图论理论基础篇 中我们讲到了 两种 图的存储方式:邻接表 和 邻接矩阵。
本题我们将带大家分别实现这两个图的存储方式。
邻接矩阵
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
本题我们会有n 个节点,因为节点标号是从1开始的,为了节点标号和下标对齐,我们申请 n + 1 * n + 1 这么大的二维数组。
邻接表
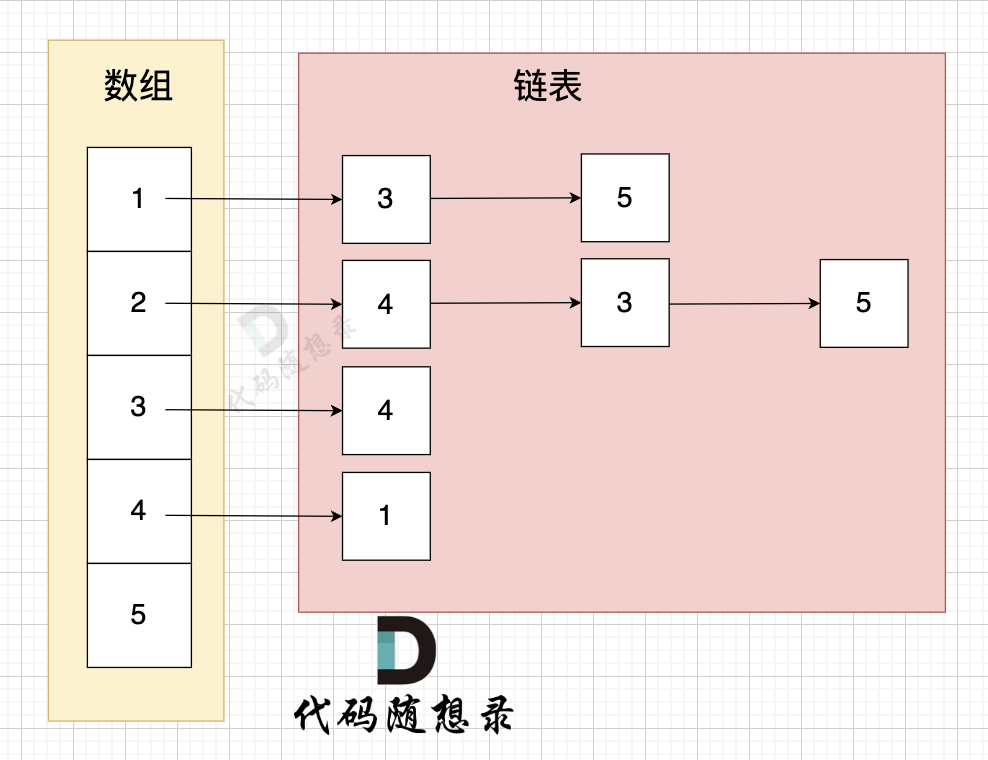
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
邻接表的构造相对邻接矩阵难理解一些。
我在 图论理论基础篇 举了一个例子:
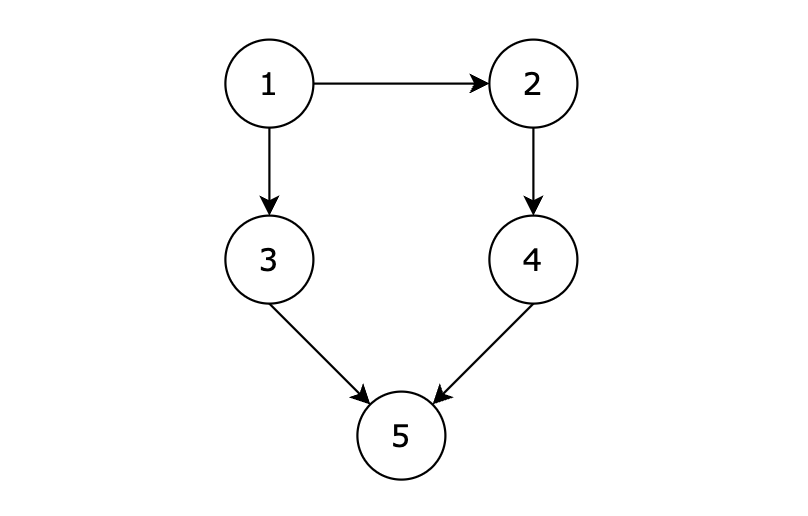
这里表达的图是:
- 节点1 指向 节点3 和 节点5
- 节点2 指向 节点4、节点3、节点5
- 节点3 指向 节点4
- 节点4指向节点1
我们需要构造一个数组,数组里的元素是一个链表。
深度优先搜索
本题是深度优先搜索的基础题目,关于深搜我在图论深搜理论基础 已经有详细的讲解,图文并茂。
关于本题我会直接使用深搜三部曲来分析,如果对深搜不够了解,建议先看 图论深搜理论基础。
深搜三部曲来分析题目:
1.确认递归函数,参数
首先我们dfs函数一定要存一个图,用来遍历的,需要存一个目前我们遍历的节点,定义为x。
还需要存一个n,表示终点,我们遍历的时候,用来判断当 x==n 时候 标明找到了终点。
(其实在递归函数的参数 不容易一开始就确定了,一般是在写函数体的时候发现缺什么,参加就补什么)至于 单一路径 和 路径集合 可以放在全局变量。
2.确认终止条件
什么时候我们就找到一条路径了?
当目前遍历的节点 为 最后一个节点 n 的时候 就找到了一条 从出发点到终止点的路径。
3.处理目前搜索节点出发的路径
接下来是走 当前遍历节点x的下一个节点。
首先是要找到 x节点指向了哪些节点呢? 遍历方式是这样的:
for i in range(1,n+1): # 遍历节点x链接的所有节点if graph[x][i] == 1: # 找到 x指向的节点,就是节点i接下来就是将 选中的x所指向的节点,加入到 单一路径来。
path.append(i) # 遍历到的节点加入到路径中来进入下一层递归
def dfs(graph, i, n) : # 进入下一层递归
最后就是回溯的过程,撤销本次添加节点的操作。
为什么要有回溯,我在图论深搜理论基础 也有详细的讲解。
方法一: 邻接矩阵写法
def dfs(graph,x,n,path,result):if x == n:result.append(path[:])returnfor i in range(1,n+1):if graph[x][i] == 1:path.append(i)dfs(graph,i,n,path,result)path.pop()def main():n,m = map(int,input().split())graph = [[0]* (n+1) for _ in range(n+1)]for i in range(m):s,t = map(int,input().split())graph[s][t] = 1result = []dfs(graph,1,n,[1],result)if not result:print(-1)else:for path in result:print(' '.join(map(str,path)))if __name__ == "__main__":main()方法二:邻接表写法
from collections import defaultdictresult = [] # 收集符合条件的路径
path = [] # 1节点到终点的路径def dfs(graph, x, n):if x == n: # 找到符合条件的一条路径result.append(path.copy())returnfor i in graph[x]: # 找到 x指向的节点path.append(i) # 遍历到的节点加入到路径中来dfs(graph, i, n) # 进入下一层递归path.pop() # 回溯,撤销本节点def main():n, m = map(int, input().split())graph = defaultdict(list) # 邻接表for _ in range(m):s, t = map(int, input().split())graph[s].append(t)path.append(1) # 无论什么路径已经是从1节点出发dfs(graph, 1, n) # 开始遍历# 输出结果if not result:print(-1)for path in result:print(' '.join(map(str, path)))if __name__ == "__main__":main()这篇关于代码随想录算法训练营第五十天 | 98. 所有可达路径的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!