iOS CoreAudio学习笔记（二）—— The Story of Sound

本文主要是介绍iOS CoreAudio学习笔记（二）—— The Story of Sound，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在上一章，我们初次尝试了CoreAudio API：它提供了什么以及怎样调用它的函数。现在是时候往回一步来看看一张更大的图：一开始CoreAudio访问的问题。

这一章将介绍基础的声音科学，它是什么，它怎样工作。事实证明，计算机的数字化天性使它们并不那么适合处理连续的模拟信号。这引导了对信号采样的思想，或者将平滑的声波斩为频率足够大的离散值，而人耳无法注意到差别。这一章覆盖了这些采样在数字化形态中是怎样被表示和整理分类的。

Making Waves

如果你在人行道上猛推一个人，那个人就会动一下而已。但是如果你在一个拥挤的地方猛推一个人，比如在音乐会上，他会碰到他前面的人然后弹回他原来的位置。由于你推的力在人群中传递，这将会触发一个连锁反应，最终穿过房间打到你的朋友。你刚刚通过一群生气的代理推了你的朋友。

在科学术语里面，一群足够近的相互反弹的物体被叫做介质，能量可以通过它们传递。你推的那个人的运动（一开始向前，然后向后）称为一个循环。完成一个循环的时间叫做周期。如果你反复地推一个人，人们相互反弹的这种模式就是一个压缩的波。

这个波有两个属性。你推这个波的力形成了波的振幅。你推这个波的速度形成了波的频率。你越频繁地推，这个波的频率就会越高。如果你改变你推的振幅和频率，你的朋友将会感受到这样的变化。你不再只是生产波，而是在通过介质传递数据。

当你对某人说话，你的声带来回移动或者振动，推动空气中的原子。这些原子相互反弹就像音乐会里面的人一样，直到它们击中你朋友的鼓膜。扬声器和麦克风就是这样做的。声音就是通过介质传递的能量而已。

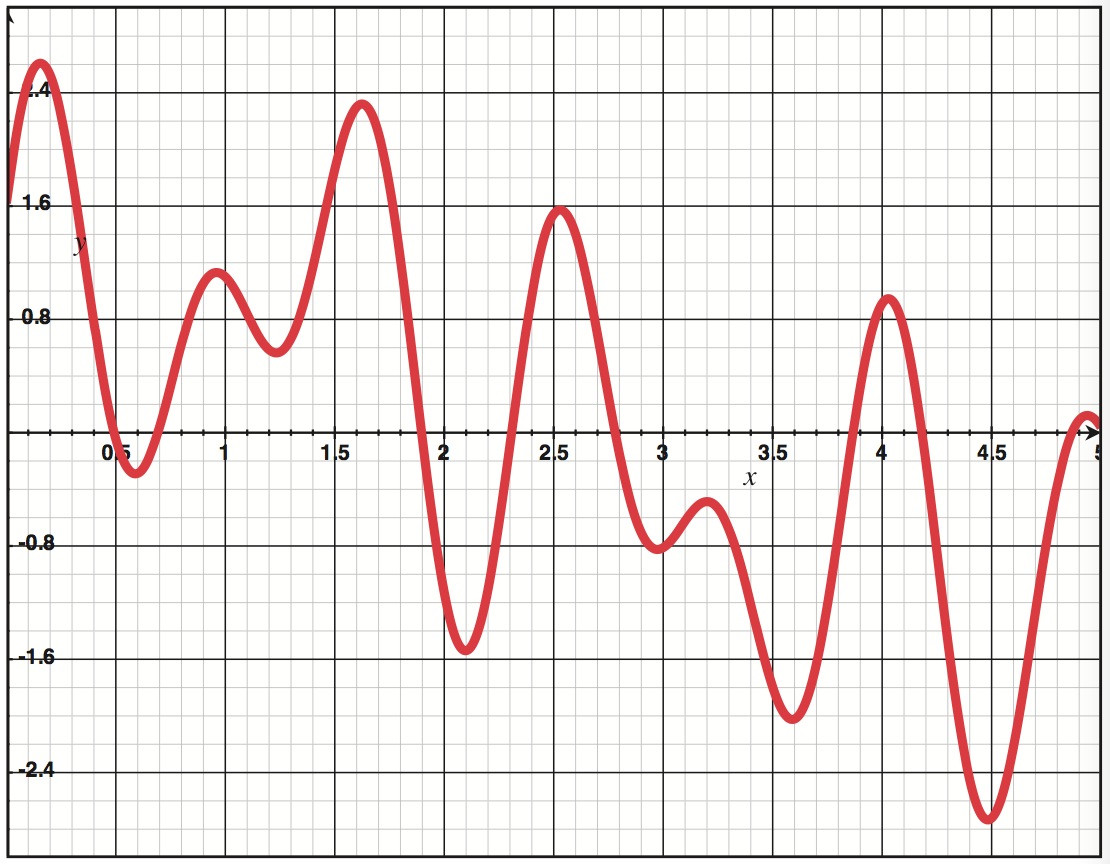
要录音的话，你所需做的就是描述声音使膜振动的方式。要播放声音的话，你需要像提供的描述那样让一个膜振动。一种描述声音的方式是基于时间画出膜的位置，如图所示。

Figure 2.1

图中央的横线代表膜静止时的状态。顶部和底部代表膜位移的最大值。随着时间从左到右移动，膜的位置一上一下。y轴代表振幅最大值的百分比，正值和负值来回变化的频率代表声音的频率。

一种表示这段声波的方法是把它的图像雕刻成一些物理对象。这种技术叫做模拟记录法，它的好处在于它将产生一个非常精确的复制品。而它的缺点在于录音会像它描述的声波那样不精确。这样的不精确来源自复制的同时播放。它同样不兼容计算机，因为计算机需要的东西要有精确的数值计算来描述。

Digital Audio

对于计算机，你需要把波通过数字来表示。你可以沿着波的路径绘制一系列（x，y）坐标点来近似这段波。如果你提供了足够多的点，你将会得到一个不错的展现。一个标准叫做脉冲编码调制(pulse code modulation, PCM) ，它每隔一段规律的时间记录一次y值，意思是x值（时间）是隐式的。其最常见的形式是线性脉冲编码调制，你指定一个代表y值最大值百分比的值。举个栗子，如果一个图表示的值从0到1，给出的一个点的y值是最大值的一半，那么你指定的值就是0.5。这种在规律的时间间隔的时候指定一个值的处理叫做采样。每个值是它本身的一个采样。

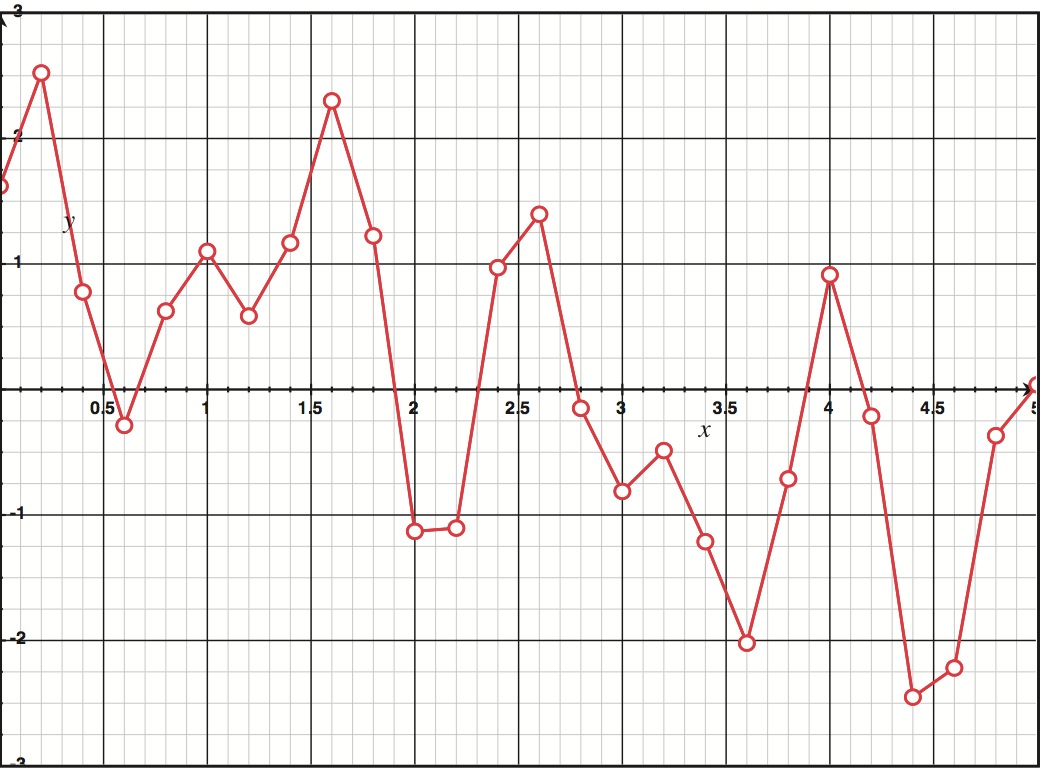
CD音质的音频采样率为44.1 kHz，也就是每秒44100个采样。一种看清这个的方法是认识到CD音质的音频每秒有44100个少于23微秒的间隙。没有任何数据存在于这些间隙中，在这段时间发生在声波上的任何东西都消失了。下图阐述了采样率是如何影响数据精确地模拟声波曲线的能力的。三张图都代表了Figure2.1的波，但是削减了采样率。如你所见，使用更少的采样会使得声波表示得更不精确。事实上，t=2.5的峰值和t=2.1的谷值以及t=4.4的数据在最后一张图中完全遗失了。

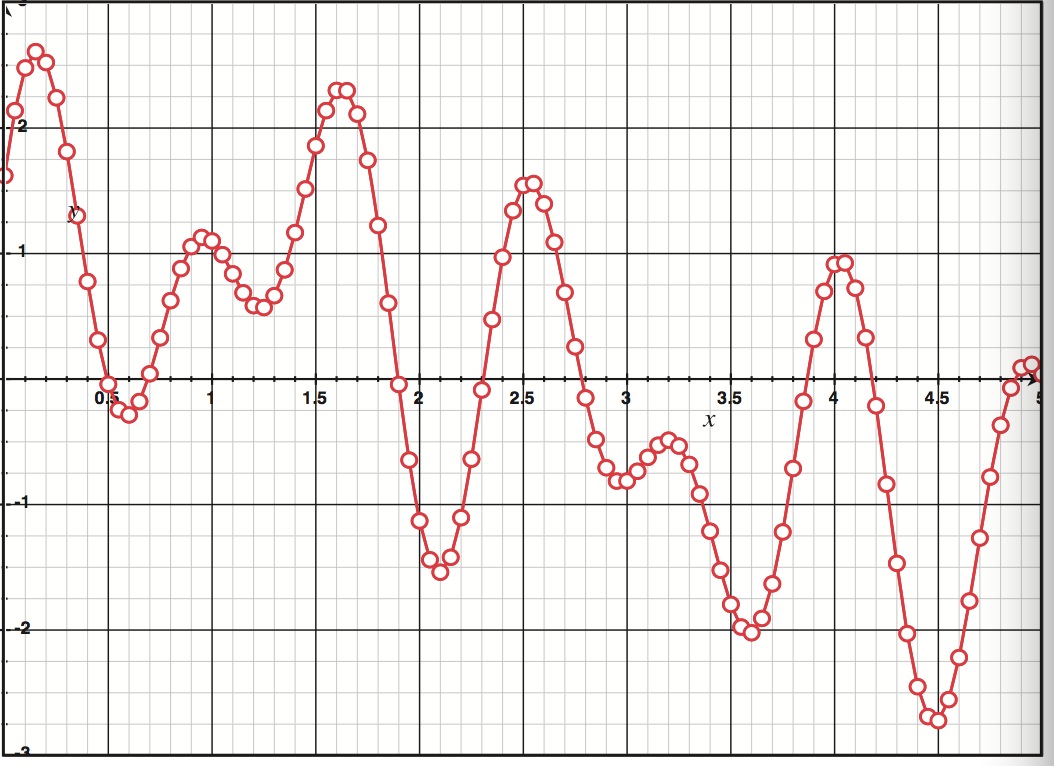
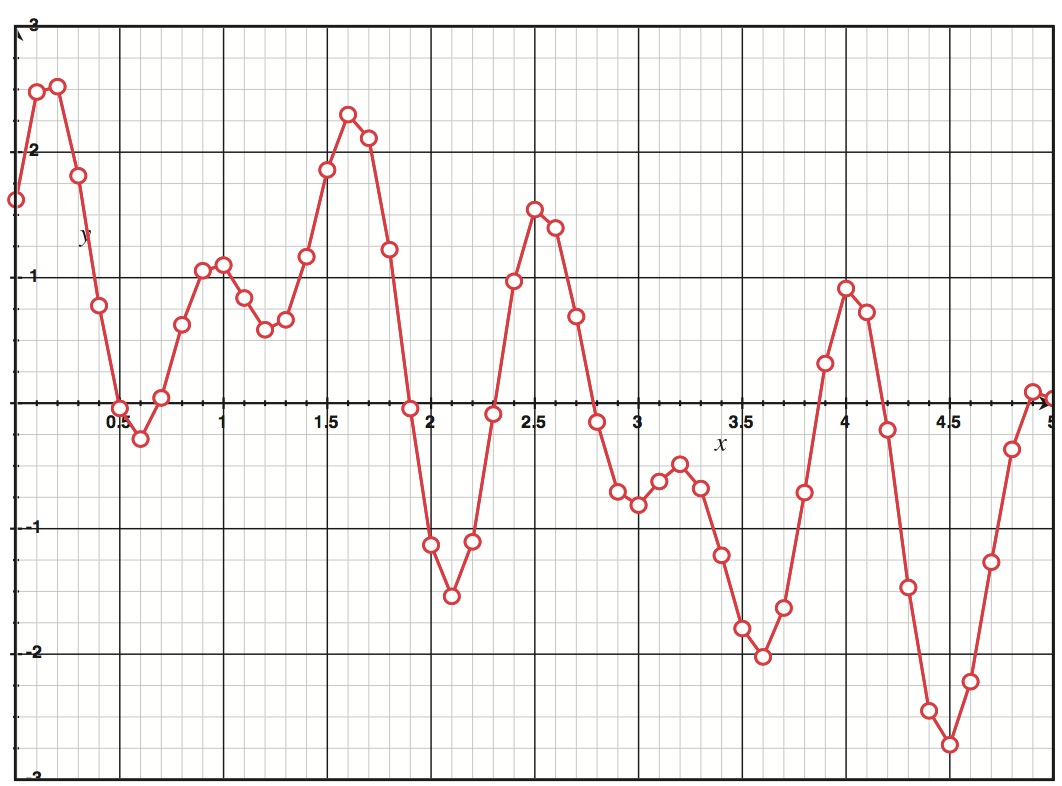
Figure 2.2 某采样率下的声波模拟

你可以通过增加更多的采样模拟的更加精确，但是知道存在一些“足够好”的粒度是很有帮助的。找到一个足够好的模拟的关键在于你听到的不是个别的采样，而是通过空气推出的声波。你听到的是频率，振动的重复形式，无论是从吉他和弦还是喉咙发出来的。你需要弄明白需要多快的采样来再现这些振动频率。

事实上你可以从奈奎斯特-香农采样定律（Nyquist-Shannon Sampling Theorem）中找到这个数字，这个定律说，如果你有一个一个函数表示没有频率能高过B Hz，那么你可以用间隔1/(2B)秒分开的点精确地呈现它。对于音频，这就意味着要再现任何频率，你需要用两倍或更高频率采样信号。

这就解释了为什么CD音质的音频的采样率为44.1 kHz。它的一半是22.05Hz，超出了绝大部分人类可以听到的频率。感知到高频率声音的能力随着年龄的增长而恶化。年轻人差不多能听到20kHz，而一个中年人可能只听得到14或者15kHz。所以通过44.1kHz的采样，你可能会丢失一些信息，但是不用担心，真正重要的其实是听众在音频信号中感知到振动频率的能力。

每一个采样代表了波的振幅，或者膜的位移，作为最大可能值的百分比。使用百分比的好处在于硬件独立性。一半就是一半，直接忽视什么被折半了。

不像整数那样越大的数需要更多的数字来表达，分数需要更多的数字来表达更小的数。写100比写10需要更多的数字，但是写1/100要比写1/10需要更多的数字。一个采样拥有多少数字叫做它的位深（像素深度）。如果两个声音的差距（最大可能位移的百分比）比采样拥有的数字还小，那么这个差距就将会丢失。

位深（每个采样拥有的bit量）乘以采样率（每秒采样的量）得到比特率（每秒bit量）。这就描述了音频1秒钟需要多少个bit。更高的比特率会提供更高质量的录音，但是那也意味着硬件需要存储和处理更多的bit。

数字高保真的根本问题在于通过给定限制的硬件找到最好的近似值。每一个不同的格式都是一系列不同的妥协解决这个问题的方法。不仅在数字音频中，更广泛地，举个栗子，在数码相片中同样有这么多问题，对于相同的格式字母汤，每种格式提供自己的解决方案。

在数字图像中，采样率被转换成了像素值，而位深则转换成了每像素的颜色值。增加一个bit将会得到两倍的收益。在图2.3中两个相邻图像的差距为1bit。

Figure 2.3

一个琐碎的实现细节是，这个比喻只适用于灰度图像。计算机不能像人类看见的那样确切地显示颜色像素。每一个颜色像素点由红、绿和蓝组成。每一点又需要它们自己的数据集，叫做通道。大多数图像格式将每一个通道的采样结合成一坨表示单个像素。

数字音频也存在这些问题。一段单声道声波就像一张灰度图一样，但是许多声音系统都有多道发声器。就像像素需要红色、蓝色和绿色作为通道一样，立体声需要左声道和右声道。环绕声增加了额外的通道。一个典型的5.1环绕声信号有6个通道：左右声道来处理前和后；一个中心通道；一个无方向通道来处理低频效果，比如贝斯。

和它们的图形同胞一样，音频格式把每个通道的一个采样结合成一坨，称为帧。鉴于一个像素代表在空间中一个区域里面所有的颜色通道，一帧代表在时间中一个时刻所有的音频通道。所以对于单声道而言，一帧只有一个采样；而对于立体声则有两个采样。如果你把多通道的声音放入一个流，则它们被称为交错模式 。对于播放这是很常见的：因为你想要同时读取所有的通道，有理的做法就是安排数据简单地这样做。然而，当处理音频（比如添加效果或者做一些其他的信号处理的时候）时，你可能想要非交错模式的音频，那么你就可以分离地关注每一个通道了。

一些音频格式将许多帧结合成分组。这一概念完全是

这篇关于iOS CoreAudio学习笔记（二）—— The Story of Sound的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---