本文主要是介绍可重入VI,VI模板和动态VI之间的差异 转,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
可重入VI
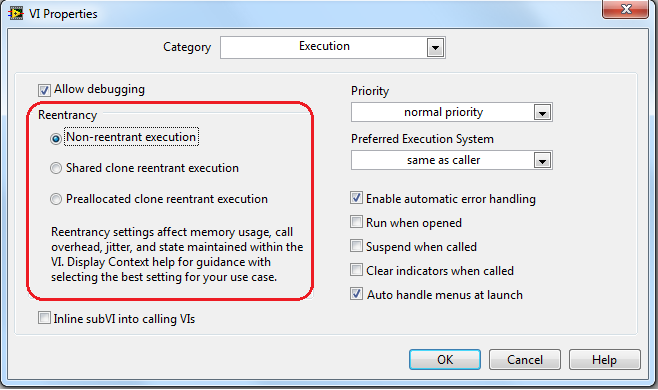
当您想要同时运行同一VI的多个实例时,将使用可重入VI。当VI不可重入时,VI只有一个数据空间。因此,一次只能有一个调用者运行VI,因此调用者可能必须“等待轮到它”时才能使用VI。这是VI的默认选项,但您可以将VI设置为可重入。其中有两种类型的重入:共享 和 预分配。
共享的可重入VI
如果选择了共享克隆可重入执行选项,则VI会具有一个数据空间池(与克隆池相同)。最初在调用VI开始时只创建两个克隆。调用者将使用其中一个数据空间,但它并不知道使用的时哪个数据空间,并且它可能是后续调用中的不同实例。当池中没有足够的数据空间(克隆)用于一定数量调用者同时调用时,将创建新的数据空间(克隆)并将其添加到池中。这里“实例之间共享克隆”中的“共享”一词意味着数据空间可以由多个调用者随时间使用。如果有20个针对SubVI的调用,但是这些调用发生的时间最多中只有两个调用同时进行,则池中只有两个数据空间,它们将在20个调用中“共享”。由于根据当前需要仅创建必要数量的克隆,因此优化了存储器使用。为了实现最快的执行速率和最佳的内存优化,建议使用此选项。
预先分配的可重入VI
如果选择了预分配克隆可重入执行选项,则每个调用者都有自己的私有数据空间(和克隆)。如果有20次调用VI,则在调用VI开始时将创建20个克隆并将其添加到池中。如果调用模式与上述调用模式类似,则可能只有两个同时忙碌。如果要对SubVI的给定实例的每次调用都使用相同的克隆(例如,如果SubVI需要将数据从这次调用保持到下次调用)的话,则使用这种类型的重入VI。共享克隆在这种情况下不起作用,因为您永远不会知道SubVI的哪个实例上次使用了您将要使用的克隆,并且存储的信息将在SubVI之间无法预测地“串扰”。 “预分配”意味着对于每次调用,都会创建该次调用的数据空间和克隆。预分配发生在VI运行之前。如果要打开同一VI的多个前面板,可重入的SubVI选项将不起作用。
如果要多次打开的VI是顶层VI,则可以将磁盘上的顶层VI复制到具有唯一名称的临时目录并打开新文件实例,没有必要复制任何SubVI。只需复制顶层VI,然后,您可以使用VI Server打开并运行副本。
模板VI
您可以将多实例面板制作成模板VI,然后每次从模板打开文件。 VI模板是具有 .vit 扩展名的VI。您可以在 文件»新建»从模板开始 下从模板创建新VI。这将创建一个具有自己内存空间的VI的新实例。它们在创建时具有不同的存储位置,且仅用作制作另一个VI的起点。然后,您需要配置新创建的VI是否可重入。
动态VI
您可以使用VI Server打开VI和VI模板。 VI Server 用于动态加载和运行VI。使用SubVI时,加载顶层VI时会加载SubVI的代码和数据空间。当您动态加载VI时,在VI服务器调用SubVI之前,不会加载其代码,而不是将其用作SubVI并在调用主程序时加载代码。这样可以在启动时节省内存。
这篇关于可重入VI,VI模板和动态VI之间的差异 转的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







