本文主要是介绍笔记:《利用Python进行数据分析》之apply的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这一节较难,十分灵活,可多花点时间
apply的简单应用
最通用的GroupBy方法是apply。
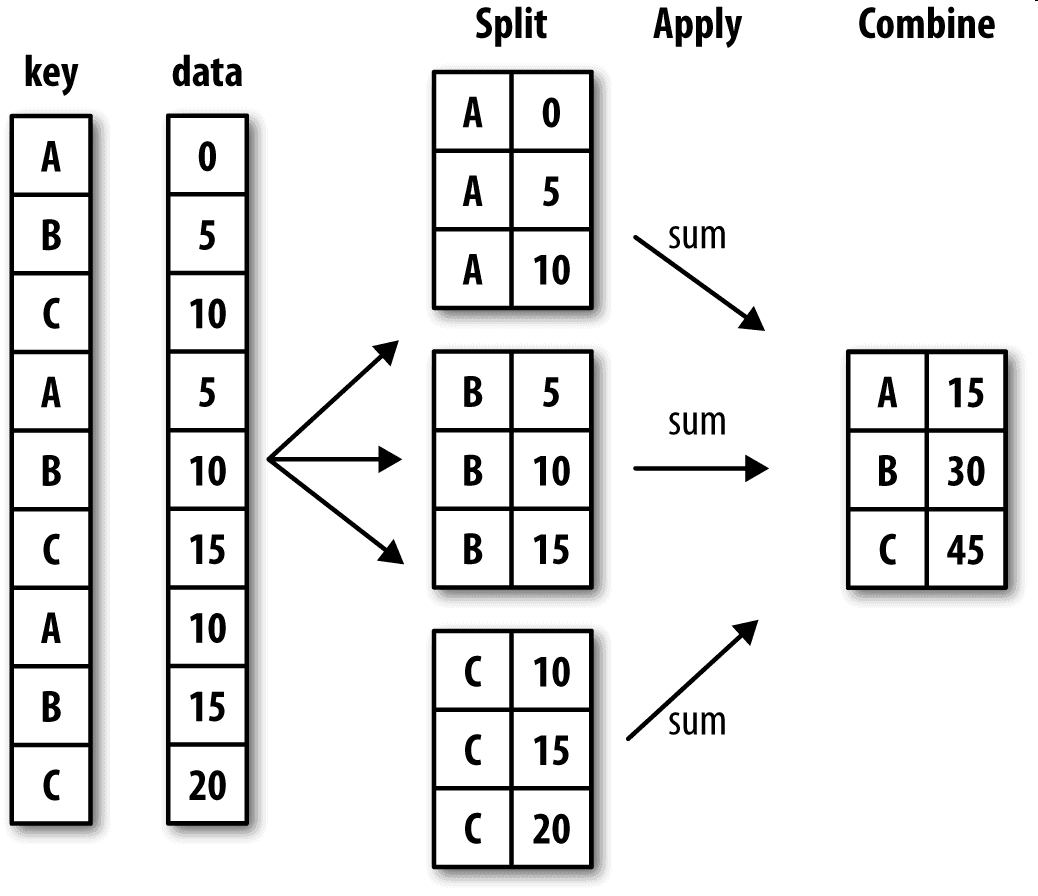
apply会将待处理的对象拆分成多个片段,然后对各片段调用传入的函数,最后尝试将各片段组合到一起。
回到之前那个小费数据集,假设你想要根据分组选出最高的5个tip_pct值。首先,编写一个选取指定列具有最大值的行的函数:
In [74]: def top(df, n=5, column='tip_pct'):....: return df.sort_values(by=column)[-n:]
In [75]: top(tips, n=6)
Out[75]: total_bill tip smoker day time size tip_pct
109 14.31 4.00 Yes Sat Dinner 2 0.279525
183 23.17 6.50 Yes Sun Dinner 4 0.280535
232 11.61 3.39 No Sat Dinner 2 0.291990
67 3.07 1.00 Yes Sat Dinner 1 0.325733
178 9.60 4.00 Yes Sun Dinner 2 0.416667
172 7.25 5.15 Yes Sun Dinner 2 0.710345现在,如果对smoker分组并用该函数调用apply,就会得到:
In [76]: tips.groupby('smoker').apply(top)
Out[76]: total_bill tip smoker day time size tip_pct
smoker
No 88 24.71 5.85 No Thur Lunch 2 0.236746185 20.69 5.00 No Sun Dinner 5 0.24166351 10.29 2.60 No Sun Dinner 2 0.252672149 7.51 2.00 No Thur Lunch 2 0.266312232 11.61 3.39 No Sat Dinner 2 0.291990
Yes 109 14.31 4.00 Yes Sat Dinner 2 0.279525183 23.17 6.50 Yes Sun Dinner 4 0.28053567 3.07 1.00 Yes Sat Dinner 1 0.325733178 9.60 4.00 Yes Sun Dinner 2 0.416667172 7.25 5.15 Yes Sun Dinner 2 0.710345这里发生了什么?top函数在DataFrame的各个片段上调用,然后结果由pandas.concat组装到一起,并以分组名称进行了标记。于是,最终结果就有了一个层次化索引,其内层索引值来自原DataFrame。
如果传给apply的函数能够接受其他参数或关键字,则可以将这些内容放在函数名后面一并传入:
In [77]: tips.groupby(['smoker', 'day']).apply(top, n=1, column='total_bill')
Out[77]: total_bill tip smoker day time size tip_pct
smoker day
No Fri 94 22.75 3.25 No Fri Dinner 2 0.142857Sat 212 48.33 9.00 No Sat Dinner 4 0.186220Sun 156 48.17 5.00 No Sun Dinner 6 0.103799Thur 142 41.19 5.00 No Thur Lunch 5 0.121389
Yes Fri 95 40.17 4.73 Yes Fri Dinner 4 0.117750Sat 170 50.81 10.00 Yes Sat Dinner 3 0.196812Sun 182 45.35 3.50 Yes Sun Dinner 3 0.077178Thur 197 43.11 5.00 Yes Thur Lunch 4 0.115982除这些基本用法之外,能否充分发挥apply的威力很大程度上取决于你的创造力。传入的那个函数能做什么全由你说了算,它只需返回一个pandas对象或标量值即可。
在GroupBy对象上调用describe:
In [78]: result = tips.groupby('smoker')['tip_pct'].describe()
In [79]: result
Out[79]: count mean std min 25% 50% 75% \
smoker
No 151.0 0.159328 0.039910 0.056797 0.136906 0.155625 0.185014
Yes 93.0 0.163196 0.085119 0.035638 0.106771 0.153846 0.195059 max
smoker
No 0.291990
Yes 0.710345
In [80]: result.unstack('smoker')
Out[80]: smoker
count No 151.000000Yes 93.000000
mean No 0.159328Yes 0.163196
std No 0.039910Yes 0.085119
min No 0.056797Yes 0.035638
25% No 0.136906Yes 0.106771
50% No 0.155625Yes 0.153846
75% No 0.185014Yes 0.195059
max No 0.291990Yes 0.710345
dtype: float64在GroupBy中,当你调用诸如describe之类的方法时,实际上只是应用了下面两条代码的快捷方式而已:
f = lambda x: x.describe()
grouped.apply(f)禁止分组键
从上面的例子中可以看出,分组键会跟原始对象的索引共同构成结果对象中的层次化索引。将group_keys=False传入groupby即可禁止该效果:
In [81]: tips.groupby('smoker', group_keys=False).apply(top)
Out[81]: total_bill tip smoker day time size tip_pct
88 24.71 5.85 No Thur Lunch 2 0.236746
185 20.69 5.00 No Sun Dinner 5 0.241663
51 10.29 2.60 No Sun Dinner 2 0.252672
149 7.51 2.00 No Thur Lunch 2 0.266312
232 11.61 3.39 No Sat Dinner 2 0.291990
109 14.31 4.00 Yes Sat Dinner 2 0.279525
183 23.17 6.50 Yes Sun Dinner 4 0.280535
67 3.07 1.00 Yes Sat Dinner 1 0.325733
178 9.60 4.00 Yes Sun Dinner 2 0.416667
172 7.25 5.15 Yes Sun Dinner 2 0.710345分位数和桶分析
pandas有一些能根据指定面元或样本分位数将数据拆分成多块的工具(比如cut和qcut)。将这些函数跟groupby结合起来,就能非常轻松地实现对数据集的桶(bucket)或分位数(quantile)分析了。以下面这个简单的随机数据集为例,我们利用cut将其装入长度相等的桶中:
In [82]: frame = pd.DataFrame({'data1': np.random.randn(1000),....: 'data2': np.random.randn(1000)})
In [83]: quartiles = pd.cut(frame.data1, 4)
In [84]: quartiles[:10]
Out[84]:
0 (-1.23, 0.489]
1 (-2.956, -1.23]
2 (-1.23, 0.489]
3 (0.489, 2.208]
4 (-1.23, 0.489]
5 (0.489, 2.208]
6 (-1.23, 0.489]
7 (-1.23, 0.489]
8 (0.489, 2.208]
9 (0.489, 2.208]
Name: data1, dtype: category
Categories (4, interval[float64]): [(-2.956, -1.23] < (-1.23, 0.489] < (0.489, 2.
208] < (2.208, 3.928]]由cut返回的Categorical对象可直接传递到groupby。因此,我们可以像下面这样对data2列做一些统计计算:
In [85]: def get_stats(group):....: return {'min': group.min(), 'max': group.max(),....: 'count': group.count(), 'mean': group.mean()}
In [86]: grouped = frame.data2.groupby(quartiles)
In [87]: grouped.apply(get_stats).unstack()
Out[87]: count max mean min
data1
(-2.956, -1.23] 95.0 1.670835 -0.039521 -3.399312
(-1.23, 0.489] 598.0 3.260383 -0.002051 -2.989741
(0.489, 2.208] 297.0 2.954439 0.081822 -3.745356
(2.208, 3.928] 10.0 1.765640 0.024750 -1.929776这些都是长度相等的桶。要根据样本分位数得到大小相等的桶,使用qcut即可。传入labels=False即可只获取分位数的编号:
# Return quantile numbers
In [88]: grouping = pd.qcut(frame.data1, 10, labels=False)
In [89]: grouped = frame.data2.groupby(grouping)
In [90]: grouped.apply(get_stats).unstack()
Out[90]: count max mean min
data1
0 100.0 1.670835 -0.049902 -3.399312
1 100.0 2.628441 0.030989 -1.950098
2 100.0 2.527939 -0.067179 -2.925113
3 100.0 3.260383 0.065713 -2.315555
4 100.0 2.074345 -0.111653 -2.047939
5 100.0 2.184810 0.052130 -2.989741
6 100.0 2.458842 -0.021489 -2.223506
7 100.0 2.954439 -0.026459 -3.056990
8 100.0 2.735527 0.103406 -3.745356
9 100.0 2.377020 0.220122 -2.064111示例:用特定于分组的值填充缺失值(重难点)
对于缺失数据的清理工作,有时你会用dropna将其替换掉,而有时则可能会希望用一个固定值或由数据集本身所衍生出来的值去填充NA值。这时就得使用fillna这个工具了。
对所有缺失值填充相同的值
在下面这个例子中,我用平均值去填充NA值:
In [91]: s = pd.Series(np.random.randn(6))
In [92]: s[::2] = np.nan
In [93]: s
Out[93]:
0 NaN
1 -0.125921
2 NaN
3 -0.884475
4 NaN
5 0.227290
dtype: float64
In [94]: s.fillna(s.mean())
Out[94]:
0 -0.261035
1 -0.125921
2 -0.261035
3 -0.884475
4 -0.261035
5 0.227290
dtype: float64对不同的分组填充不同的值
假设你需要对不同的分组填充不同的值。一种方法是将数据分组,并使用apply和一个能够对各数据块调用fillna的函数即可。下面是一些有关美国几个州的示例数据,这些州又被分为东部和西部:
In [95]: states = ['Ohio', 'New York', 'Vermont', 'Florida',....: 'Oregon', 'Nevada', 'California', 'Idaho']
In [96]: group_key = ['East'] * 4 + ['West'] * 4
In [97]: data = pd.Series(np.random.randn(8), index=states)
In [98]: data
Out[98]:
Ohio 0.922264
New York -2.153545
Vermont -0.365757
Florida -0.375842
Oregon 0.329939
Nevada 0.981994
California 1.105913
Idaho -1.613716
dtype: float64# 将一些值设为缺失:In [99]: data[['Vermont', 'Nevada', 'Idaho']] = np.nan
In [100]: data
Out[100]:
Ohio 0.922264
New York -2.153545
Vermont NaN
Florida -0.375842
Oregon 0.329939
Nevada NaN
California 1.105913
Idaho NaN
dtype: float64
In [101]: data.groupby(group_key).mean()
Out[101]:
East -0.535707
West 0.717926
dtype: float64我们可以用分组平均值去填充NA值:
In [102]: fill_mean = lambda g: g.fillna(g.mean())
In [103]: data.groupby(group_key).apply(fill_mean)
Out[103]:
Ohio 0.922264
New York -2.153545
Vermont -0.535707
Florida -0.375842
Oregon 0.329939
Nevada 0.717926
California 1.105913
Idaho 0.717926
dtype: float64另外,也可以在代码中预定义各组的填充值。由于分组具有一个name属性,所以我们可以拿来用一下:
In [104]: fill_values = {'East': 0.5, 'West': -1}
In [105]: fill_func = lambda g: g.fillna(fill_values[g.name])
In [106]: data.groupby(group_key).apply(fill_func)
Out[106]:
Ohio 0.922264
New York -2.153545
Vermont 0.500000
Florida -0.375842
Oregon 0.329939
Nevada -1.000000
California 1.105913
Idaho -1.000000
dtype: float64示例:分组加权平均数和相关系数
根据groupby的“拆分-应用-合并”范式,可以进行DataFrame的列与列之间或两个Series之间的运算(比如分组加权平均)。以下面这个数据集为例,它含有分组键、值以及一些权重值:
In [114]: df = pd.DataFrame({'category': ['a', 'a', 'a', 'a',.....: 'b', 'b', 'b', 'b'],.....: 'data': np.random.randn(8),.....: 'weights': np.random.rand(8)})
In [115]: df
Out[115]: category data weights
0 a 1.561587 0.957515
1 a 1.219984 0.347267
2 a -0.482239 0.581362
3 a 0.315667 0.217091
4 b -0.047852 0.894406
5 b -0.454145 0.918564
6 b -0.556774 0.277825
7 b 0.253321 0.955905然后可以利用category计算分组加权平均数:
In [116]: grouped = df.groupby('category')
In [117]: get_wavg = lambda g: np.average(g['data'], weights=g['weights'])
In [118]: grouped.apply(get_wavg)
Out[118]:
category
a 0.811643
b -0.122262
dtype: float64另一个例子,考虑一个来自Yahoo!Finance的数据集,其中含有几只股票和标准普尔500指数(符号SPX)的收盘价:
In [119]: close_px = pd.read_csv('examples/stock_px_2.csv', parse_dates=True,.....: index_col=0)
In [120]: close_px.info()
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 2214 entries, 2003-01-02 to 2011-10-14
Data columns (total 4 columns):
AAPL 2214 non-null float64
MSFT 2214 non-null float64
XOM 2214 non-null float64
SPX 2214 non-null float64
dtypes: float64(4)
memory usage: 86.5 KB
In [121]: close_px[-4:]
Out[121]: AAPL MSFT XOM SPX
2011-10-11 400.29 27.00 76.27 1195.54
2011-10-12 402.19 26.96 77.16 1207.25
2011-10-13 408.43 27.18 76.37 1203.66
2011-10-14 422.00 27.27 78.11 1224.58来做一个比较有趣的任务:计算一个由日收益率(通过百分数变化计算)与SPX之间的年度相关系数组成的DataFrame。下面是一个实现办法,我们先创建一个函数,用它计算每列和SPX列的成对相关系数:
In [122]: spx_corr = lambda x: x.corrwith(x['SPX'])接下来,我们使用pct_change计算close_px的百分比变化:
In [123]: rets = close_px.pct_change().dropna()最后,我们用年对百分比变化进行分组,可以用一个一行的函数,从每行的标签返回每个datetime标签的year属性:
In [124]: get_year = lambda x: x.year
In [125]: by_year = rets.groupby(get_year)
In [126]: by_year.apply(spx_corr)
Out[126]: AAPL MSFT XOM SPX
2003 0.541124 0.745174 0.661265 1.0
2004 0.374283 0.588531 0.557742 1.0
2005 0.467540 0.562374 0.631010 1.0
2006 0.428267 0.406126 0.518514 1.0
2007 0.508118 0.658770 0.786264 1.0
2008 0.681434 0.804626 0.828303 1.0
2009 0.707103 0.654902 0.797921 1.0
2010 0.710105 0.730118 0.839057 1.0
2011 0.691931 0.800996 0.859975 1.0当然,你还可以计算列与列之间的相关系数。这里,我们计算Apple和Microsoft的年相关系数:
In [127]: by_year.apply(lambda g: g['AAPL'].corr(g['MSFT']))
Out[127]:
2003 0.480868
2004 0.259024
2005 0.300093
2006 0.161735
2007 0.417738
2008 0.611901
2009 0.432738
2010 0.571946
2011 0.581987
dtype: float64示例:组级别的线性回归
顺着上一个例子继续,你可以用groupby执行更为复杂的分组统计分析,只要函数返回的是pandas对象或标量值即可。例如,我可以定义下面这个regress函数(利用statsmodels计量经济学库)对各数据块执行普通最小二乘法(Ordinary Least Squares,OLS)回归:
import statsmodels.api as sm
def regress(data, yvar, xvars):Y = data[yvar]X = data[xvars]X['intercept'] = 1.result = sm.OLS(Y, X).fit()return result.params现在,为了按年计算AAPL对SPX收益率的线性回归,执行:
In [129]: by_year.apply(regress, 'AAPL', ['SPX'])
Out[129]: SPX intercept
2003 1.195406 0.000710
2004 1.363463 0.004201
2005 1.766415 0.003246
2006 1.645496 0.000080
2007 1.198761 0.003438
2008 0.968016 -0.001110
2009 0.879103 0.002954
2010 1.052608 0.001261
2011 0.806605 0.001514这篇关于笔记:《利用Python进行数据分析》之apply的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




