本文主要是介绍Markdown语法与Latex公式汇总,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 基本语法
1.1 标题
语法如下:

效果如下:

1.2 字体样式
| 语法 | 效果 |
|---|---|
普通正文字体 | 普通正文字体 |
*倾斜字体* | 倾斜字体 |
**加粗字体** | 加粗字体 |
***倾斜加粗字体*** | 倾斜字体 |
~~划线字体~~ |
1.3 分割线
语法如下:

效果如下:

1.4 引用
语法如下:

效果如下:

1.5 列表
有序列表
语法如下:

效果如下:

无序列表
语法如下:

效果如下:

1.6 表格
新建表格
语法如下:

效果如下:

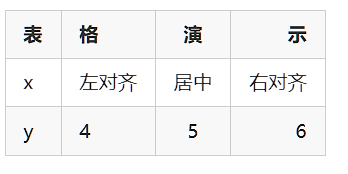
调整表格对齐样式
我们可以指定表格单元格的对齐方式,冒号在左边表示左对齐,右边表示有对齐,两边都有表示居中
语法如下:

效果如下:
1.7 代码块
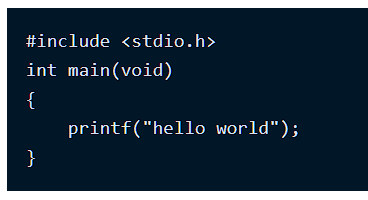
使用Tab缩进
语法如下:

效果如下:
行内式代码块
语法如下:

效果如下:

多行代码块及语法高亮显示
语法如下:

效果如下:

2 进阶语法
2.1 特殊符号
| 语法 | 效果 |
|---|---|
❤ | ❤ |
✓ | ✓ |
☀ | ☀ |
★ | ★ |
2.2 字体样式和字体颜色
| 语法 | 效果 |
|---|---|
<font face="黑体">黑体字体</font> | 黑体字体 |
<font face="微软雅黑">微软雅黑字体</font> | 微软雅黑字体 |
<font face="STCAIYUN">华文彩云字体</font> | 华文彩云字体 |
<font color=#ff0000 face="STCAIYUN">红色华文彩云字体</font> | 红色华文彩云字体 |
3 Latex公式
3.1 Latex基础语法
上下标
| 语法 | 效果 |
|---|---|
$数学符号^{上标}$ | 数学符 号 上标 数学符号^{上标} 数学符号上标 |
$数学符号_{下标}$ | 数学符 号 下标 数学符号_{下标} 数学符号下标 |
$数学符号^{上标}_{下标}$ | 数学符 号 下标 上标 数学符号^{上标}_{下标} 数学符号下标上标 |
正负号
| 语法 | 效果 |
|---|---|
$\pm$ | ± \pm ± |
乘、除、分式、开方
| 语法 | 效果 |
|---|---|
$\times$ | × \times × |
$\cdot$ | ⋅ \cdot ⋅ |
$\div$ | ÷ \div ÷ |
$\frac{分子}{分母}$ | 分子 分母 \frac{分子}{分母} 分母分子 |
$\cfrac{分子}{分母}$ | 分子 分母 \cfrac{分子}{分母} 分母分子 |
$\sqrt[根指数]{被开方数}$ | 被开方数 根指数 \sqrt[根指数]{被开方数} 根指数被开方数 |
小于大于不等于约等于
| 语法 | 效果 |
|---|---|
$\leqslant$ | ⩽ \leqslant ⩽ |
$\geqslant$ | ⩾ \geqslant ⩾ |
$\ne$ | ≠ \ne = |
$\approx$ | ≈ \approx ≈ |
逻辑推导
| 语法 | 效果 |
|---|---|
$\because$ | ∵ \because ∵ |
$\therefore$ | ∴ \therefore ∴ |
$\to$ | → \to → |
$\implies$ | ⟹ \implies ⟹ |
$\iff$ | ⟺ \iff ⟺ |
三角形、相似、全等、垂直
| 语法 | 效果 |
|---|---|
$\triangle$ | △ \triangle △ |
$\sim$ | ∼ \sim ∼ |
$\cong$ | ≅ \cong ≅ |
$\perp$ | ⊥ \perp ⊥ |
向量
| 语法 | 效果 |
|---|---|
$\vec{a}$ | a ⃗ \vec{a} a |
$\overrightarrow{ab}$ | a b → \overrightarrow{ab} ab |
$\overleftarrow{ab}$ | a b ← \overleftarrow{ab} ab |
无穷
| 语法 | 效果 |
|---|---|
$\infty$ | ∞ \infty ∞ |
数学关系
| 语法 | 效果 |
|---|---|
$\propto$ | ∝ \propto ∝ |
$\in$ | ∈ \in ∈ |
$\notin$ | ∉ \notin ∈/ |
$\forall$ | ∀ \forall ∀ |
$\exists$ | ∃ \exists ∃ |
平均值
| 语法 | 效果 |
|---|---|
$\overline{x}$ | x ‾ \overline{x} x |
导数
| 语法 | 效果 |
|---|---|
$x'$ | x ′ x' x′ |
角度
| 语法 | 效果 |
|---|---|
$\theta$ | θ \theta θ |
$角度数值^\circ$ | 角度数 值 ∘ 角度数值^\circ 角度数值∘ |
$\angle$ | ∠ \angle ∠ |
函数
| 语法 | 效果 |
|---|---|
$\sin\theta$ | sin θ \sin\theta sinθ |
$\cos\theta$ | cos θ \cos\theta cosθ |
$\tan\theta$ | tan θ \tan\theta tanθ |
$\ln x$ | ln x \ln x lnx |
$\lg x$ | lg x \lg x lgx |
$\log_a X$ | log a X \log_a X logaX |
弧
| 语法 | 效果 |
|---|---|
$\overset{\frown} {AB}$ | A B ⌢ \overset{\frown} {AB} AB⌢ |
极限
| 语法 | 效果 |
|---|---|
$\lim\limits_{x \to 0}$ | lim x → 0 \lim\limits_{x \to 0} x→0lim |
求和
| 语法 | 效果 |
|---|---|
$\sum\limits_{i=1}^{n}$ | ∑ i = 1 n \sum\limits_{i=1}^{n} i=1∑n |
积分
| 语法 | 效果 |
|---|---|
$\int_{0}^{1}$ | ∫ 0 1 \int_{0}^{1} ∫01 |
二项式
| 语法 | 效果 |
|---|---|
${\binom{n}{k}}$ | ( n k ) {\binom{n}{k}} (kn) |
${\dbinom{n}{k}}$ | ( n k ) {\dbinom{n}{k}} (kn) |
3.2 希腊字母
| 语法 | 效果 | 语法 | 效果 |
|---|---|---|---|
$\alpha$ | α \alpha α | ||
$\beta$ | β \beta β | ||
$\gamma$ | γ \gamma γ | ||
$\delta$ | δ \delta δ | $\Delta$ | Δ \Delta Δ |
$\eta$ | η \eta η | ||
$\lambda$ | λ \lambda λ | ||
$\mu$ | μ \mu μ | ||
$\nu$ | ν \nu ν | ||
$\pi$ | π \pi π | ||
$\rho$ | ρ \rho ρ | ||
$\sigma$ | σ \sigma σ | ||
$\omega$ | ω \omega ω | ||
$\epsilon$ | ϵ \epsilon ϵ | ||
$\varphi$ | φ \varphi φ | ||
$\phi$ | ϕ \phi ϕ | $\Phi$ | Φ \Phi Φ |
这篇关于Markdown语法与Latex公式汇总的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






