float 或 double 运算的时候会有精度丢失的风险？

2024-09-01 15:20
文章标签 丢失 运算 风险 double 精度 float

本文主要是介绍float 或 double 运算的时候会有精度丢失的风险？，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

《阿里巴巴 Java 开发手册》中提到：“浮点数之间的等值判断，基本数据类型不能用 == 来比较，包装数据类型不能用 equals 来判断”。“为了避免精度丢失，可以使用 BigDecimal 来进行浮点数的运算”。

浮点数的运算竟然还会有精度丢失的风险吗？确实会！

示例代码：

float a = 2.0f - 1.9f;
float b = 1.8f - 1.7f;
System.out.println(a);// 0.100000024
System.out.println(b);// 0.099999905
System.out.println(a == b);// false

这个和计算机保存浮点数的机制有很大关系。我们知道计算机是二进制的，而且计算机在表示一个数字时，宽度是有限的，无限循环的小数存储在计算机时，只能被截断，所以就会导致小数精度发生损失的情况。这也就是解释了为什么浮点数没有办法用二进制精确表示。

就比如说十进制下的 0.2 就没办法精确转换成二进制小数：

// 0.2 转换为二进制数的过程为，不断乘以 2，直到不存在小数为止，
// 在这个计算过程中，得到的整数部分从上到下排列就是二进制的结果。
0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0（发生循环）
...

那我们怎样来解决这样的问题呢？

JDK开发人员在很早就遇到了这个问题，并在JDK1.3起给我们提供了一种新的处理精确值的类BigDecimal，BigDecimal是标准的类，在编译器中不需要特殊支持，它可以表示任意精度的小数，并对它们进行计算。在内部，可以用任意精度任何范围的值和一个
换算因子来表示 BigDecimal，换算因子表示左移小数点多少位，从而得到所期望范围内的值

BigDecimal 介绍

BigDecimal 可以实现对浮点数的运算，不会造成精度丢失。

通常情况下，大部分需要浮点数精确运算结果的业务场景（比如涉及到钱的场景）都是通过 BigDecimal 来做的。

想要解决浮点数运算精度丢失这个问题，可以直接使用 BigDecimal 来定义浮点数的值，然后再进行浮点数的运算操作即可。

BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
BigDecimal c = BigDecimal.valueOf(0.8);BigDecimal x = a.subtract(b);
BigDecimal y = b.subtract(c);System.out.println(x.compareTo(y));// 0

BigDecimal 常见方法

创建

在使用 BigDecimal 时，为了防止精度丢失，推荐使用它的BigDecimal(String val)构造方法或者 BigDecimal.valueOf(double val) 静态方法来创建对象。

《阿里巴巴 Java 开发手册》对这部分内容也有提到，如下图所示。

public static BigDecimal valueOf(double val) {return new BigDecimal(Double.toString(val));
}

加减乘除

  • add 方法：两个 BigDecimal 对象相加
  • subtract 方法：两个 BigDecimal 对象相减
  • multiply 方法：两个 BigDecimal 对象相乘
  • divide 方法：两个 BigDecimal 对象相除。
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
System.out.println(a.add(b));// 1.9
System.out.println(a.subtract(b));// 0.1
System.out.println(a.multiply(b));// 0.90
System.out.println(a.divide(b));// 无法除尽，抛出 ArithmeticException 异常
System.out.println(a.divide(b, 2, RoundingMode.HALF_UP));// 1.11

这里需要注意的是，在使用 divide 方法的时候尽量使用 3 个参数版本，并且RoundingMode 不要选择 UNNECESSARY，否则很可能会遇到 ArithmeticException（无法除尽出现无限循环小数的时候），其中 scale 表示要保留几位小数，roundingMode 代表保留规则。

public BigDecimal divide(BigDecimal divisor, int scale, RoundingMode roundingMode) {return divide(divisor, scale, roundingMode.oldMode);
}

保留几位小数 setScale

通过 setScale方法设置保留几位小数以及保留规则。保留规则如上，不需要记，IDEA 会提示。

BigDecimal m = new BigDecimal("1.255433");
BigDecimal n = m.setScale(3, RoundingMode.HALF_DOWN);
System.out.println(n);// 1.255

保留规则非常多，这里列举几种:

public enum RoundingMode {// 2.5 -> 3 , 1.6 -> 2// -1.6 -> -2 , -2.5 -> -3UP(BigDecimal.ROUND_UP),//远离零方向舍入，无论正负// 2.5 -> 2 , 1.6 -> 1// -1.6 -> -1 , -2.5 -> -2DOWN(BigDecimal.ROUND_DOWN),//向零方向舍入，直接去掉小数部分。// 2.5 -> 3 , 1.6 -> 2// -1.6 -> -1 , -2.5 -> -2CEILING(BigDecimal.ROUND_CEILING),//向正无穷方向舍入。// 2.5 -> 2 , 1.6 -> 1// -1.6 -> -2 , -2.5 -> -3FLOOR(BigDecimal.ROUND_FLOOR),//向负无穷方向舍入。// 2.5 -> 3 , 1.6 -> 2// -1.6 -> -2 , -2.5 -> -3HALF_UP(BigDecimal.ROUND_HALF_UP),//四舍五入，小数部分 >= 0.5 向上，否则向下。//......
}

等值比较问题

《阿里巴巴 Java 开发手册》中提到：

BigDecimal 使用 equals() 方法进行等值比较出现问题的代码示例：

BigDecimal a = new BigDecimal("1");
BigDecimal b = new BigDecimal("1.0");
System.out.println(a.equals(b));//false

这是因为BigDecimal的 equals() 方法不仅仅会比较值的大小（value）还会比较精度（scale），而 compareTo() 方法比较的时候会忽略精度。

1.0 的 scale 是 1，1 的 scale 是 0，因此 a.equals(b) 的结果是 false。

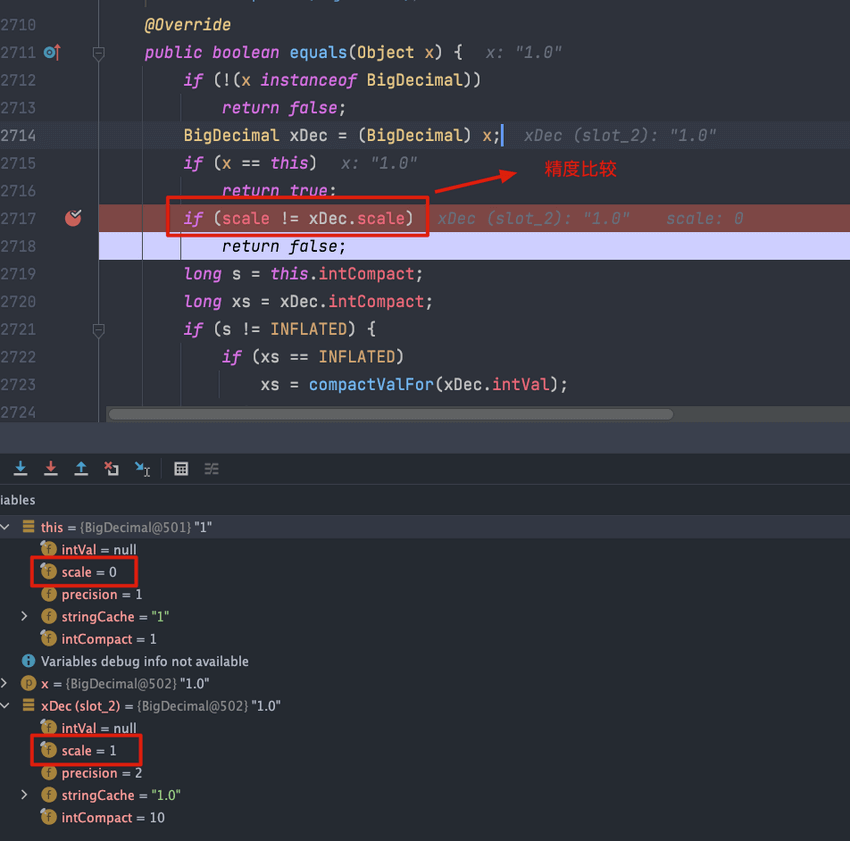
compareTo() 方法可以比较两个 BigDecimal 的值：
a.compareTo(b) : 返回 -1 表示 a 小于 b，0 表示 a 等于 b ， 1 表示 a 大于 b。

BigDecimal a = new BigDecimal("1");
BigDecimal b = new BigDecimal("1.0");
System.out.println(a.compareTo(b));//0

BigDecimal 存在的性能问题

由于其精确性和灵活性，BigDecimal 在某些场景下同样可能会带来性能问题。

BigDecimal的性能问题主要源于以下几点：

  1. 内存占用：BigDecimal 对象的内存占用较大，尤其是在处理大数字时。每个 BigDecimal 实例都需要维护其精度和标度等信息，这会导致内存开销增加。
  2. 不可变性：BigDecimal 是不可变类，每次进行运算或修改值时都会生成一个新的 BigDecimal 实例。这意味着频繁的操作可能会导致大量的对象创建和垃圾回收，对性能造成一定的影响。
  3. 运算复杂性：由于 BigDecimal 要求精确计算，它在执行加、减、乘、除等运算时会比较复杂。这些运算需要更多的计算和处理时间，相比原生的基本类型，会带来一定的性能损耗。

性能问题验证：

@Slf4j
public class BigDecimalEfficiency {//执行次数public static int REPEAT_TIMES = 10000000;// 转BigDecimal 类型计算public static double computeByBigDecimal(double a, double b) {BigDecimal result = BigDecimal.valueOf(0);BigDecimal decimalA = BigDecimal.valueOf(a);BigDecimal decimalB = BigDecimal.valueOf(b);for (int i = 0; i < REPEAT_TIMES; i++) {result = result.add(decimalA.multiply(decimalB));}return result.doubleValue();}// 转double 类型计算public static double computeByDouble(double a, double b) {double result = 0;for (int i = 0; i < REPEAT_TIMES; i++) {result += a * b;}return result;}public static void main(String[] args) {long start1 = System.nanoTime();double result1 = computeByBigDecimal(0.120001110034, 11.22);long end1 = System.nanoTime();long start2 = System.nanoTime();double result2 = computeByDouble(0.120001110034, 11.22);long end2 = System.nanoTime();long timeUsed1 = (end1 - start1);long timeUsed2 = (end2 - start2);log.info("result by BigDecimal:{},time used:{}", result1, timeUsed1);log.info("result by Double:{},time used:{}", result2, timeUsed2);log.info("timeUsed1/timeUsed2=" + timeUsed1 / timeUsed2);}
}

运行结果：

性能优化策略

BigDecimal 性能问题优化策略，可以考虑以下几点优化策略：

  1. 避免频繁的对象创建：尽量复用 BigDecimal 对象，而不是每次运算都创建新的实例。可以使用 BigDecimal 的 setScale() 方法设置精度和舍入模式，而不是每次都创建新的对象。
  2. 使用原生类型替代：对于一些不需要精确计算的场景，可以使用原生类型（如 int、double、long）来进行运算，以提高性能。只在最后需要精确结果时再转换为 BigDecimal。
  3. 使用适当的缓存策略：对于频繁使用的 BigDecimal 对象，可以考虑使用缓存来避免重复创建和销毁。例如，使用对象池或缓存来管理常用的 BigDecimal 对象，以减少对象创建和垃圾回收的开销。
  4. 考虑并行计算：对于大规模的计算任务，可以考虑使用并行计算来提高性能。Java 8 提供了 Stream API 和并行流（parallel stream），可以方便地实现并行计算。

需要根据具体的应用场景和需求来权衡精确性和性能，选择合适的处理方式。在对性能要求较高的场景下，可以考虑使用其他更适合的数据类型或算法来替代 BigDecimal。在需要精度计算的情况下，也不能因为BigDecimal存在一定的性能问题二选择弃用，顾此失彼。

BigDecimal 工具类分享

网上有一个使用人数比较多的 BigDecimal 工具类，提供了多个静态方法来简化 BigDecimal 的操作。源码：

public class BigDecimalUtil {/*** 默认除法运算精度*/private static final int DEF_DIV_SCALE = 10;private BigDecimalUtil() {}/*** 提供精确的加法运算。** @param v1 被加数* @param v2 加数* @return 两个参数的和*/public static double add(double v1, double v2) {BigDecimal b1 = BigDecimal.valueOf(v1);BigDecimal b2 = BigDecimal.valueOf(v2);return b1.add(b2).doubleValue();}/*** 提供精确的减法运算。** @param v1 被减数* @param v2 减数* @return 两个参数的差*/public static double subtract(double v1, double v2) {BigDecimal b1 = BigDecimal.valueOf(v1);BigDecimal b2 = BigDecimal.valueOf(v2);return b1.subtract(b2).doubleValue();}/*** 提供精确的乘法运算。** @param v1 被乘数* @param v2 乘数* @return 两个参数的积*/public static double multiply(double v1, double v2) {BigDecimal b1 = BigDecimal.valueOf(v1);BigDecimal b2 = BigDecimal.valueOf(v2);return b1.multiply(b2).doubleValue();}/*** 提供（相对）精确的除法运算，当发生除不尽的情况时，精确到小数点以后10位，以后的数字四舍五入。** @param v1 被除数* @param v2 除数* @return 两个参数的商*/public static double divide(double v1, double v2) {return divide(v1, v2, DEF_DIV_SCALE);}/*** 提供（相对）精确的除法运算。当发生除不尽的情况时，由scale参数指定精度，以后的数字四舍五入。** @param v1    被除数* @param v2    除数* @param scale 表示表示需要精确到小数点以后几位。* @return 两个参数的商*/public static double divide(double v1, double v2, int scale) {if (scale < 0) {throw new IllegalArgumentException("The scale must be a positive integer or zero");}BigDecimal b1 = BigDecimal.valueOf(v1);BigDecimal b2 = BigDecimal.valueOf(v2);return b1.divide(b2, scale, RoundingMode.HALF_EVEN).doubleValue();}/*** 提供精确的小数位四舍五入处理。** @param v     需要四舍五入的数字* @param scale 小数点后保留几位* @return 四舍五入后的结果*/public static double round(double v, int scale) {if (scale < 0) {throw new IllegalArgumentException("The scale must be a positive integer or zero");}BigDecimal b = BigDecimal.valueOf(v);BigDecimal one = new BigDecimal("1");return b.divide(one, scale, RoundingMode.HALF_UP).doubleValue();}/*** 提供精确的类型转换(Float)** @param v 需要被转换的数字* @return 返回转换结果*/public static float convertToFloat(double v) {BigDecimal b = new BigDecimal(v);return b.floatValue();}/*** 提供精确的类型转换(Int)不进行四舍五入** @param v 需要被转换的数字* @return 返回转换结果*/public static int convertsToInt(double v) {BigDecimal b = new BigDecimal(v);return b.intValue();}/*** 提供精确的类型转换(Long)** @param v 需要被转换的数字* @return 返回转换结果*/public static long convertsToLong(double v) {BigDecimal b = new BigDecimal(v);return b.longValue();}/*** 返回两个数中大的一个值** @param v1 需要被对比的第一个数* @param v2 需要被对比的第二个数* @return 返回两个数中大的一个值*/public static double returnMax(double v1, double v2) {BigDecimal b1 = new BigDecimal(v1);BigDecimal b2 = new BigDecimal(v2);return b1.max(b2).doubleValue();}/*** 返回两个数中小的一个值** @param v1 需要被对比的第一个数* @param v2 需要被对比的第二个数* @return 返回两个数中小的一个值*/public static double returnMin(double v1, double v2) {BigDecimal b1 = new BigDecimal(v1);BigDecimal b2 = new BigDecimal(v2);return b1.min(b2).doubleValue();}/*** 精确对比两个数字** @param v1 需要被对比的第一个数* @param v2 需要被对比的第二个数* @return 如果两个数一样则返回0，如果第一个数比第二个数大则返回1，反之返回-1*/public static int compareTo(double v1, double v2) {BigDecimal b1 = BigDecimal.valueOf(v1);BigDecimal b2 = BigDecimal.valueOf(v2);return b1.compareTo(b2);}}

总结

浮点数没有办法用二进制精确表示，因此存在精度丢失的风险。不过，Java 提供了BigDecimal 来操作浮点数。BigDecimal 的实现利用到了 BigInteger （用来操作大整数）, 所不同的是 BigDecimal 加入了小数位的概念。

这篇关于float 或 double 运算的时候会有精度丢失的风险？的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1127310。

相关文章

【Prometheus】PromQL向量匹配实现不同标签的向量数据进行运算

【Prometheus】PromQL向量匹配实现不同标签的向量数据进行运算

✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯，先赞后看哦~🎈🎈 🏆 作者简介：景天科技苑 🏆《头衔》：大厂架构师，华为云开发者社区专家博主，阿里云开发者社区专家博主，CSDN全栈领域优质创作者，掘金优秀博主，51CTO博客专家等。 🏆《博客》：Python全栈，前后端开发，小程序开发，人工智能，js逆向，App逆向，网络系统安全，数据分析，Django，fastapi
阅读更多...
uva 575 Skew Binary（位运算）

uva 575 Skew Binary（位运算）

求第一个以（2^(k+1)-1)为进制的数。 数据不大，可以直接搞。 代码： #include <stdio.h>#include <string.h>const int maxn = 100 + 5;int main(){char num[maxn];while (scanf("%s", num) == 1){if (num[0] == '0')break;int len =
阅读更多...
C 标准库 - `＜float.h＞`

C 标准库 - `＜float.h＞`

C 标准库 - <float.h> 概述 <float.h> 是 C 标准库中的一个头文件，它定义了与浮点数类型相关的宏。这些宏提供了关于浮点数的属性信息，如精度、最小和最大值、以及舍入误差等。这个头文件对于需要精确控制浮点数行为的程序非常有用，尤其是在数值计算和科学计算领域。 主要宏 <float.h> 中定义了许多宏，下面列举了一些主要的宏： FLT_RADIX：定义了浮点数的基数。
阅读更多...
C# double[] 和Matlab数组MWArray[]转换

C# double[] 和Matlab数组MWArray[]转换

C# double[] 转换成MWArray[], 直接赋值就行             MWNumericArray[] ma = new MWNumericArray[4];             double[] dT = new double[] { 0 };             double[] dT1 = new double[] { 0,2 };
阅读更多...
【Java中的位运算和逻辑运算详解及其区别】

【Java中的位运算和逻辑运算详解及其区别】

Java中的位运算和逻辑运算详解及其区别 在 Java 编程中，位运算和逻辑运算是常见的两种操作类型。位运算用于操作整数的二进制位，而逻辑运算则是处理布尔值 (boolean) 的运算。本文将详细讲解这两种运算及其主要区别，并给出相应示例。 应用场景了解 位运算和逻辑运算的设计初衷源自计算机底层硬件和逻辑运算的需求，它们分别针对不同的处理对象和场景。以下是它们设计的初始目的简介：
阅读更多...
位运算:带带孩子吧，孩子很强的！

位运算:带带孩子吧，孩子很强的！

快速进制 在聊到位运算之前，不妨先简单过一遍二进制的东西。熟悉二进制和十进制的快速转换确实是掌握位运算的基础，因为位运算直接在二进制位上进行操作。如果不熟悉二进制表示，很难直观理解位运算的效果。 这里主要涉及二进制和十进制之间的互相转换。 十进制转二进制 十进制转二进制可以使用常见的 除2取余法 进行。每次将十进制除以2并记录所得余数，直到商为0，然后再将记录的余数 从下往上排列即
阅读更多...
快速幂运算的一些模板

快速幂运算的一些模板

这里用递归和循环两种做法来做。 简单来说，快速幂就是把底数扩大，指数缩小，比如2*2=4；计算2的幂时，就可以转换成4的幂来运算，这样可以避免在计算大的数据时爆int的现象  //递归int power(int a,int n){int ans;if(n==2) ans=1;else{ans=power(a*a,n/2);if(n%2==1) ans*=a;}return ans;}
阅读更多...
俩个float数之间比较大小

俩个float数之间比较大小

需求：俩个标识金额的浮点数比较大小。 问题：相等无法成立。经过var_dump()打印，俩个浮点数数值 一样大。 解决：把标识金额的浮点数乘以100，抓换成整形，在做比较。即可使相等成立
阅读更多...
Anthropic 创始人 Dario Amodei 谈：关于护城河与风险，AI 大很难直接替代人

Anthropic 创始人 Dario Amodei 谈：关于护城河与风险，AI 大很难直接替代人

护城河的迷思   近期，Anthropic创始人Dario Amodei与投资人Erik Torenberg进行了一场引人关注的对话。他们探讨了AI的护城河与潜在风险。话说，护城河就像酒水的保质期，过了时间就得小心别翻车。Amodei提到，AI虽有强大的潜力，但短期内难以完全替代人类的智慧。这可让很多人松了一口气，毕竟机器发热总比人心复杂，听着都觉得不舒服。 聪明与控制的博弈   Dar
阅读更多...
高精度计算----减法运算(浮点型)

高精度计算----减法运算(浮点型)

基于上一贴，修改减法运算适合于高精度浮点型计算。 因为减法比加法难度大一点，考虑的地方也要多一些，可能代码有欠缺，欢迎指出。 运算说明： 1、相减函数依旧没改变，包括上一贴的判断被减数与减数的大小函数也没变。 2、增加两个函数，取小数位数函数和结果处理（回归小数点）函数 3、与加法浮点高精度运算相比，这里改变较多的是结果处理函数，加法加完后，位数不减反增，而且最多增一位。减法会消失掉好多
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2