排序算法4之归并排序

本文主要是介绍排序算法4之归并排序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

归并排序

归并排序是建立在归并操作上的一种排序算法，该算法采用分治的思想（divide and conquer）。就是先将序列进行分裂成一个个子序列，使得每个子序列都是有序的，然后再将所有的子序列整合成一个完整的序列。所以整个算法分为两部分，分裂和合并。分裂比较简单，最容易想到的就是折半分解，直至每个子序列是一个单独的数为止。合并就可能麻烦一点。

合并
假设存在两个已经排列好的子序列$\{a_1,a_2,a_3……a_n\}$和$\{b_1,b_2,b_3……b_m\}$。我们逐个比较两个子序列中项目的大小，将关键字较小的项目放入一个临时数组中，然后从对应的子序列删除放入的项目，当某个子序列为空时，就可以将另外一个子序列的全部项目依次放入临时数组中。然后利用临时数组给$\{c_1,c_2,c_3……c_{n+m}\}$赋值。

void MemeryArray(int* p,int first,int middle,int end,int* tmp)
{int i=first;//第一个子序列的起始位置int m=middle;//第一个子序列的终止位置int j=middle+1;//第二个子序列的起始位置int n=end;//第二个子序列的终止位置int k=0;while(i<=m&&j<=n){if(p[i]<p[j])tmp[k++]=p[i++];elsetmp[k++]=p[j++];}//将较小的项目放入临时数组tmpwhile(i<=m)tmp[k++]=p[i++];while(j<=n)tmp[k++]=p[j++];//将剩余的某一子序列全部放入临时数组for(int i=0;i<k;i++)//利用临时数组对原本的序列进行赋值p[first+i]=tmp[i];
}

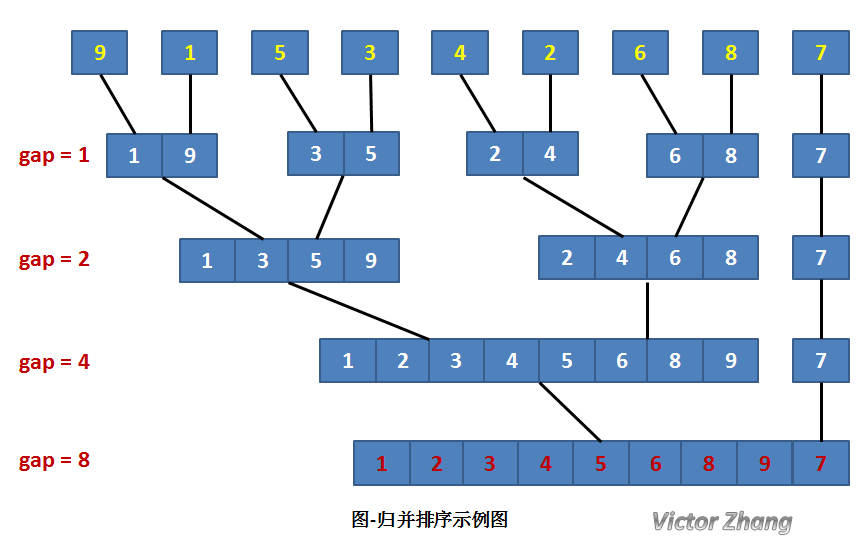
上图可以很直接的说明归并排序的思想，下面是完整的归并排序的code

#include<iostream>
using namespace std;
void MemeryArray(int* p,int first,int middle,int end,int* tmp)
{int i=first;int m=middle;int j=middle+1;int n=end;int k=0;while(i<=m&&j<=n){if(p[i]<p[j])tmp[k++]=p[i++];elsetmp[k++]=p[j++];}while(i<=m)tmp[k++]=p[i++];while(j<=n)tmp[k++]=p[j++];for(int i=0;i<k;i++)p[first+i]=tmp[i];
}//合并操作void mergeSort(int* p,int first,int end,int* tmp)
{if(first<end)//递归操作的终止条件就是first>=end{int middle=(first+end)/2;mergeSort(p,first,middle,tmp);//分解mergeSort(p,middle+1,end,tmp);//分解MemeryArray(p,first,middle,end,tmp);//合并}
}
bool MergeSort(int* p,int length)
{int* q=new int[length];//由于每次调用归并排序都需要一个临时数组，为了避免麻烦，我们直接创建一个较大的临时数组，供所有的归并排序使用。if(q==NULL)return false;mergeSort(p,0,length-1,q);delete[] q;return true;
}
int main()
{int data[5]={5,4,3,2,1};MergeSort(data,sizeof(data)/sizeof(data[0]));for(int i=0;i<sizeof(data)/sizeof(data[0]);i++)cout<<data[i]<<endl;return 0;}

从上面可以分析出来，归并排序的总共会递归调用$log_2(length)$次，而每次调用的主要时间代价就是合并，从合并函数我们知道，每次的需要赋值$2*length$次，所以时间复杂度$\Omega(nlog(n))$;空间复杂度，由于需要额外开辟一个临时数组，所以空间复杂度仍然是$\Omega(n)$;同时归并排序是一种稳定排序。

这篇关于排序算法4之归并排序的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---