本文主要是介绍统计学习-决策树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
决策树(decision tree)是一种基本的分类和回归方法。
主要优点:模型具有可读性(直观),分类速度快。
决策树学习通常包含三个步骤,特征选择,决策树的生成和决策树的剪枝。经典的决策树算法包括:Quinlan在1986年提出的ID3算法,1993年提出的C4.5算法以及由Breiman等人在1984年提出的CART算法。
决策树的模型
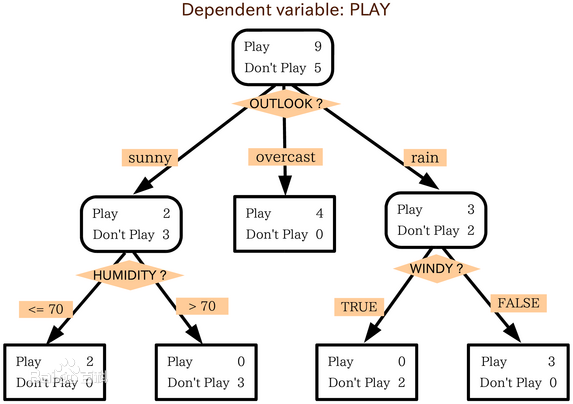
分类决策树模型是一种描述对实例进行分类的树形结构。用决策树分类,从根节点出发,对实例的某一个特征进行测试,根据测试结果将实例分配到其子节点,递归进行直至到某叶子节点,最后将实例分到叶子节点的类中。下图就是一个依据天气进行来判断是否playing的决策树:
特征选择
通常特征选择的准则是信息增益或者信息增益比。
信息增益:
在信息论与概率统计中,熵(entropy)是表示随机变量不确定性的度量。设 X 是一个取有限个值得离散随机变量,其概率分布为:
则随机变量 X 的熵定义为:
1.熵越大,随机变量的不确定性越大;
2.理论上当随机变量是均匀分布时不确定性最大,对应的信息熵 log(n)
下图是二元信息熵的分布图:
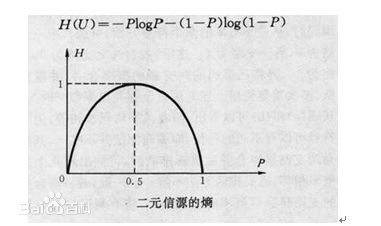
1.信息熵 H(p)∈[0,1]
2.当 H(p)=0 ,说明随机变量完全确定;
3.当 H(p)=1 ,说明随机变量不确定最大;
经验熵: H(p)=−∑ni=1pilog(pi)
经验条件熵: H(Y|X)=∑ni=1piH(Y|X=xi)
特征A对数据集D的信息增益g(D,A)代表了特征A对数据集D的不确定性减少的程度,定义如下 :
信息增益: g(D,A)=H(D)−H(D|A)
下表是一个贷款申请的样本数据,分别求出经验熵和经验条件熵,从而确定根节点处的特征:
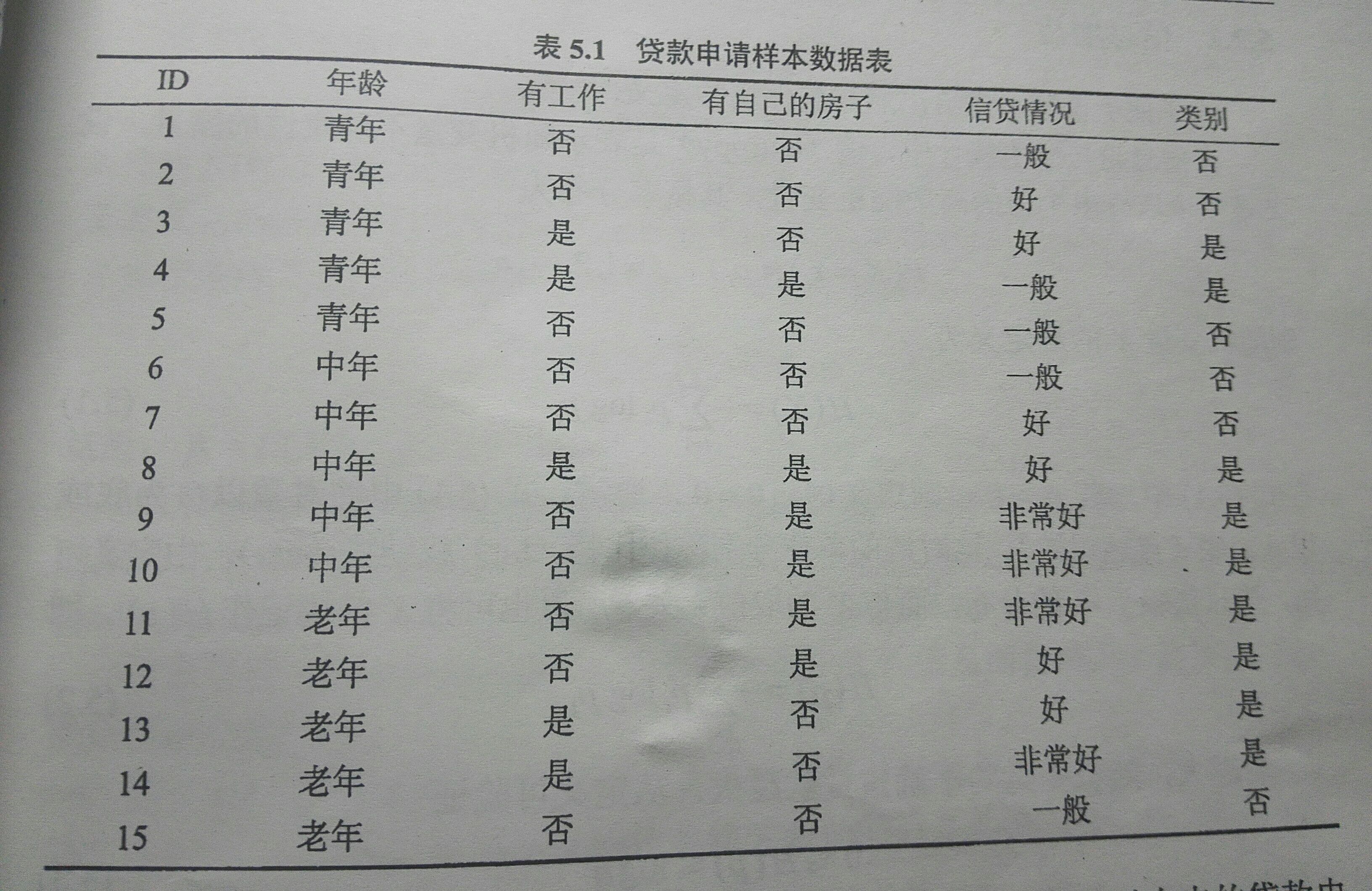
经验熵 H(p)=−∑ni=1pilog(pi)=−[615log615+915log915]=0.971 ;
经验条件熵:
H(Y|年龄)=p青年H(Y|X=青年)+p中年H(Y|X=中年)+p老年H(Y|X=老年)=515H(Y|X=青年)+515H(Y|X=中年)+515H(Y|X=老年)=515(−(35log35+25log25))+515(−(25log25+35log35))+515(−(15log15+45log45))=0.888
故 g(D,年龄)=0.971−0.888=0.083
同理可以计算:
g(D,有工作)=0.324
g(D,有房子)=0.420
g(D,信贷情况)=0.363
对比发现有自己的房子的信息增益最大,故在根节点处将选择“是否有自己的房子”作为选择特征。
信息增益比
以信息增益作为划分训练数据集的特征,存在偏向于选择取值较多的特征的问题,使用信息增益比(information gain ratio)可以对这一个问题进行矫正。定义如下:
gR(D,A)=g(D,A)HA(D)
其中 HA(D)=−∑ni=1|Di||D|log2|Di||D| ,n是特征A取值的个数。比如对于 A=年龄 , HA(D)=−(515log515+515log515+515log515)=log23
决策树的生成
1.ID3 算法
ID 3算法只有树的生成,所以该算法生成的树容易过拟合。
2.C4.5算法只是在ID3的基础上,用信息增益比进行特征选择;
决策树的剪枝
决策树生成算法通过递归地产生决策树,直到不能继续下去为止。这样产生的树的容易出现过拟合的现象,导致训练模型泛化能力不足,我们可以通过剪枝(pruning)简化模型,提高其泛化能力。
而决策树的剪枝往往通过极小化决策树整体损失函数来实现,所以我们
首先需要定义决策树的整体损失函数:
设树T的叶子节点个数 |T| , t 是树
Cα(T)=∑|T|t=1NtHt(T)+α|T|=C(T)+α|T|
前者表示模型对训练数据的预测误差,即模型和与训练数据的拟合程度(假设某一个叶子节点对应的样本点都是同一类,那么该叶子节点对应的 Ht(T)=0 ,也就说明带来的损失函数为0),后者代表模型的复杂度(比较直观,叶子节点越多,说明模型越复杂), α 控制两者之间的影响。
输入:生成算法产生的整个树T,参数α
输出:修剪后的子树
1.计算每个节点的经验熵
2.递归地从叶子节点向上回溯
设一组叶子节点回缩到其父节点之前与之后的整体树分别为TA和TB,计算对应的损失函数值,如果剪枝后使得损失函数值减小,说明该剪枝是有效的。其他剪枝方法比如:Reduced-Error Pruning(REP,错误率降低剪枝)
和Pessimistic Error Pruning(PEP,悲观剪枝)
可以参考该文。
CART生成(classification and regression tree)
决策树的生成就是递归地构建二叉决策树的过程。对回归树用平方误差最小化准则,对分类树用基尼指数(Gini index)最小化准则,进行特征选择,生成二叉树。
1.回归树的生成
假设 X 和
回归树的模型: f(x)=∑Mm=1cmI(x∈Rm) ,
其中输入空间由 M个Rm单元 划分,根据每个样本 x 落于哪个单元进行回归预测;每个单元的确定,由
minj,s[minc1∑xi∈R1(j,s)(yi−c1)2+minc2∑xi∈R2(j,s)(yi−c2)2]
其中 c1≈ave(yi|xi∈R1(j,s)) , c2≈ave(yi|xi∈R2(j,s)) ;固定 j ,我们可以得到对应的最优切分点,从而得到一个二元组
2.分类树的生成
基尼指数:分类问题中,假设有K个类,样本点属于第k类的概率为 pk ,则概率分布的基尼指数定义为: Gini(p)=∑Kk=1pk(1−pk)=1−∑Kk=1p2k ,基尼指数同信息熵一样代表了数据集合的不确定性,后面的过程同C4.5的过程是类似的,在这里就不再赘述。
这篇关于统计学习-决策树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!